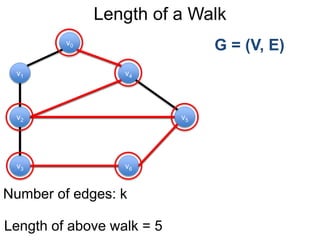
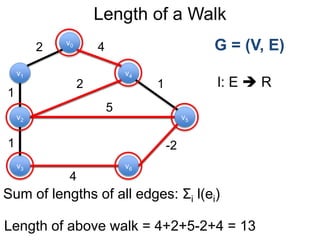
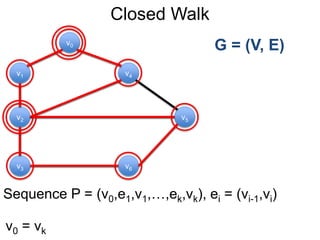
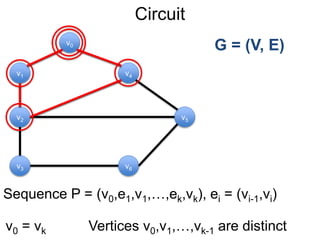
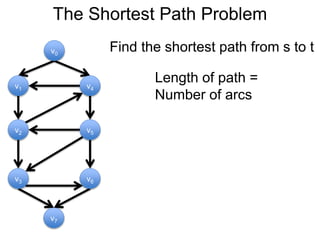
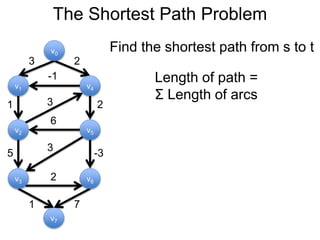
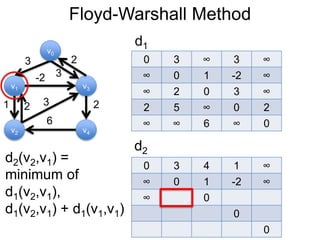
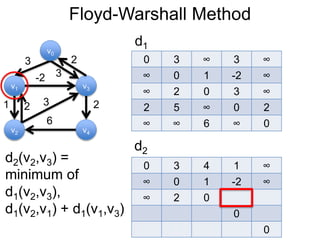
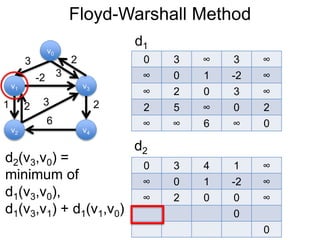
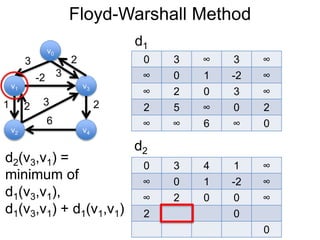
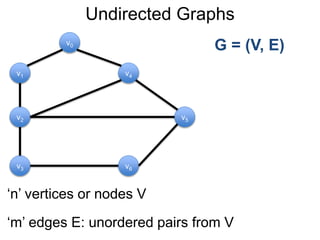
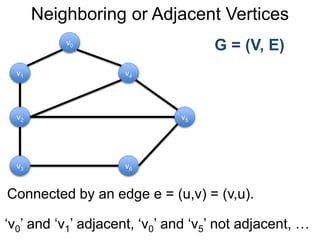
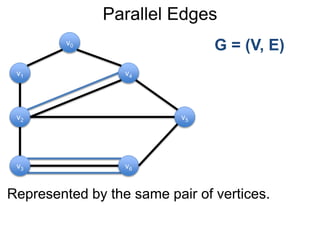
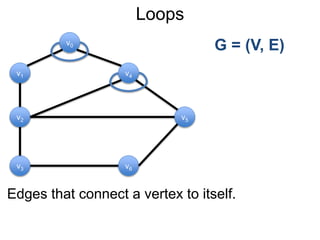
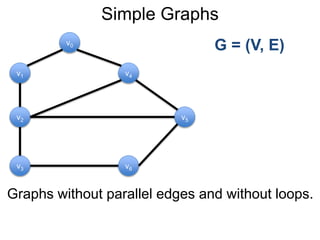
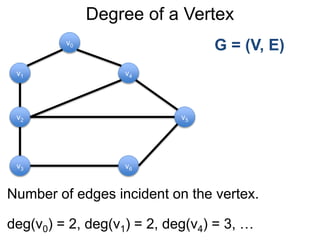
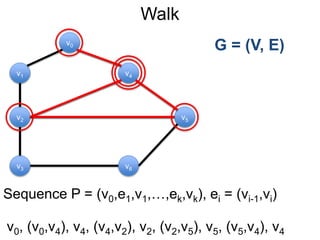
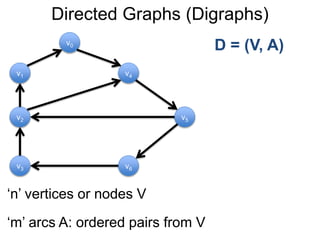
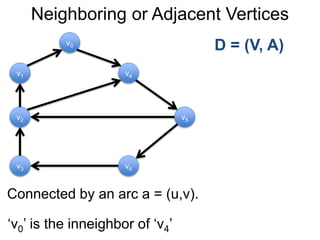
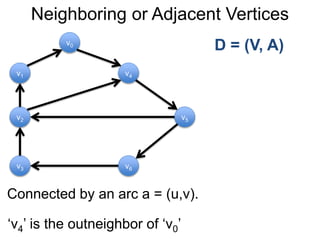
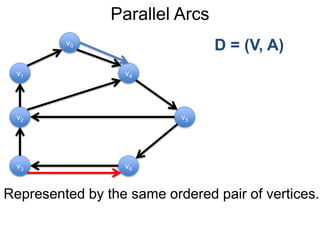
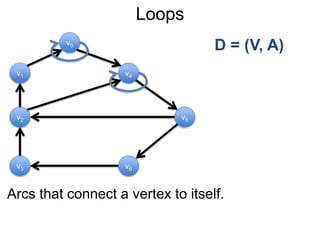
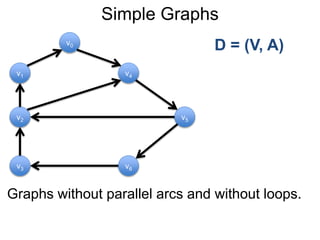
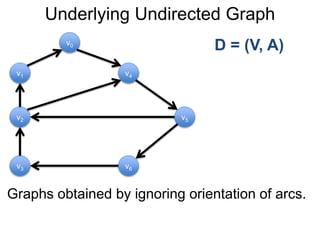
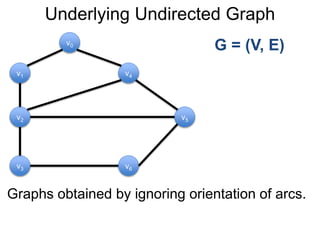
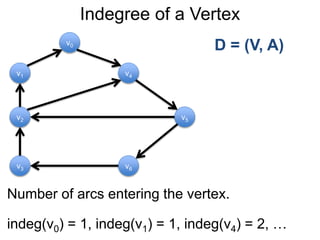
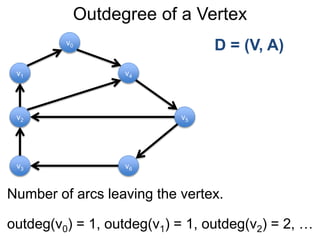
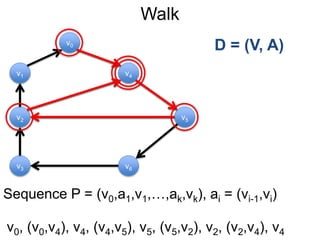
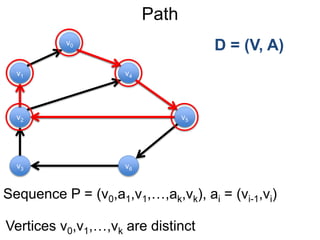
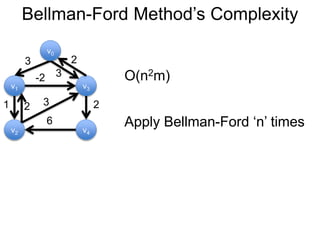
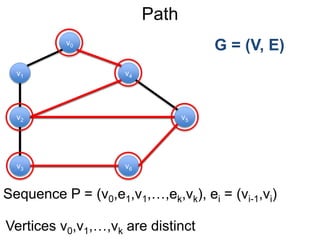
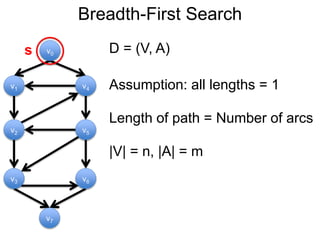
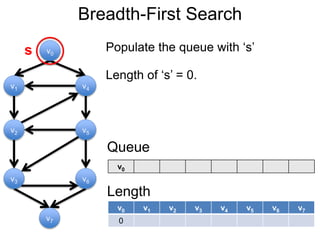
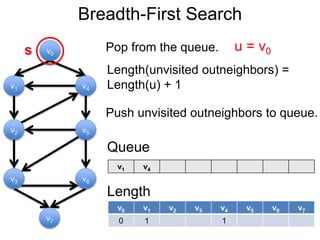
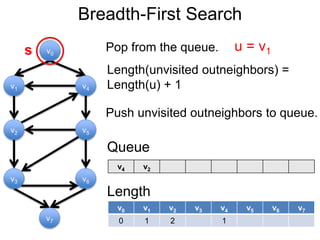
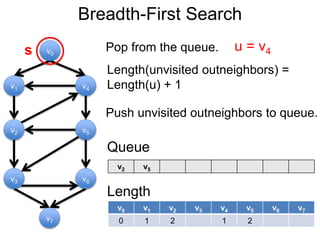
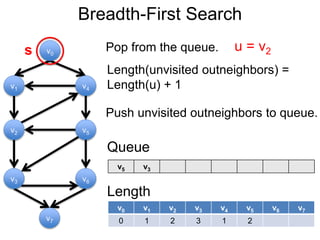
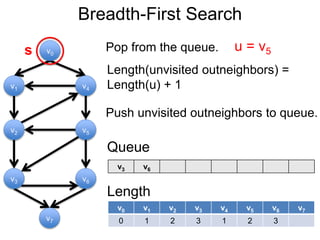
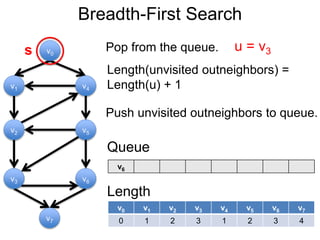
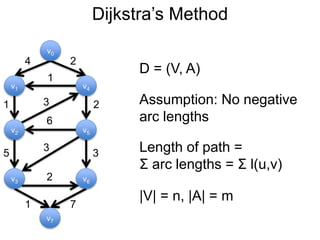
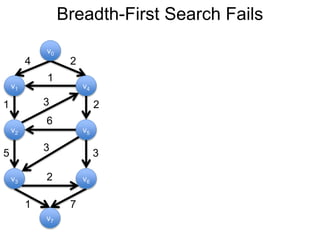
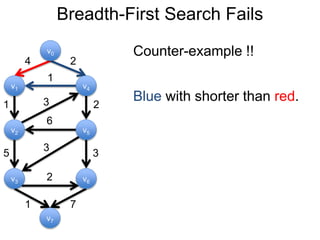
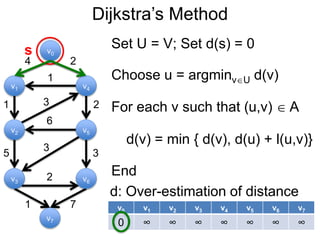
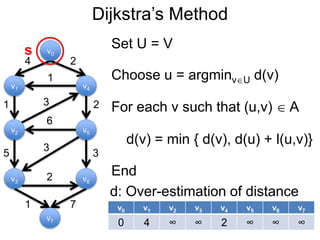
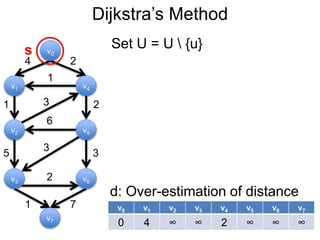
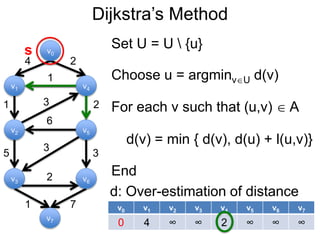
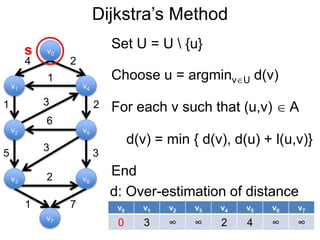
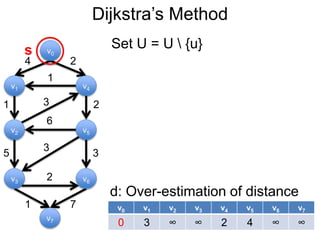
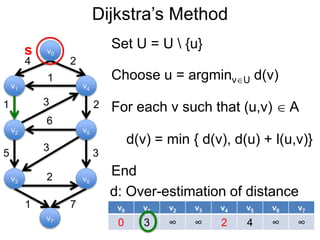
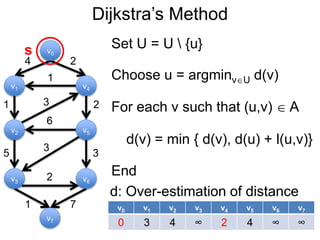
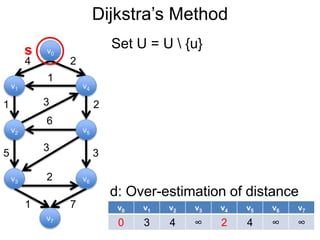
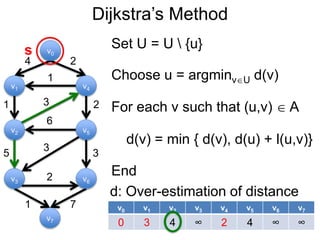
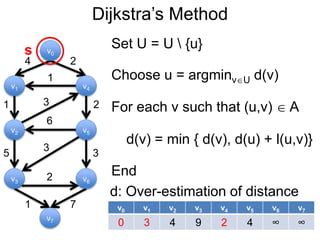
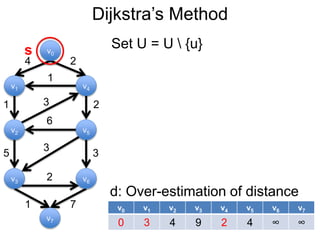
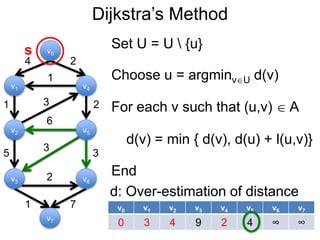
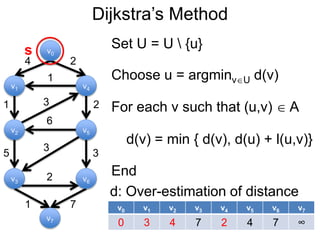
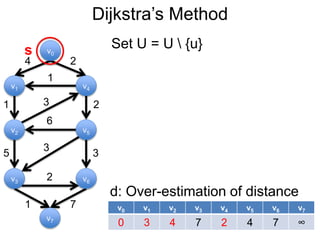
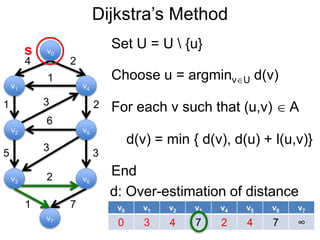
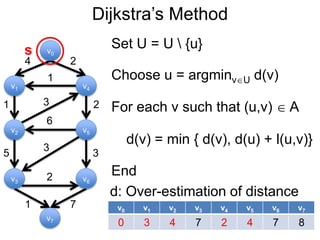
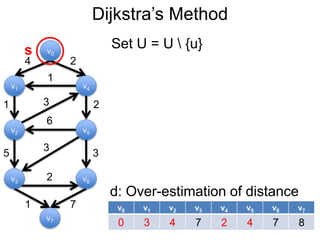
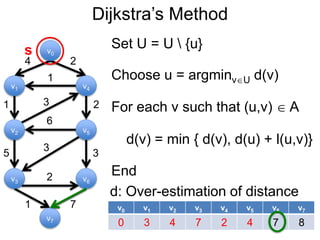
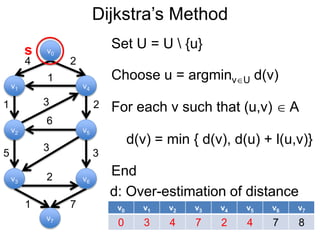
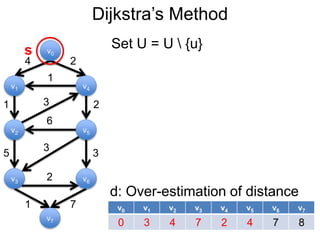
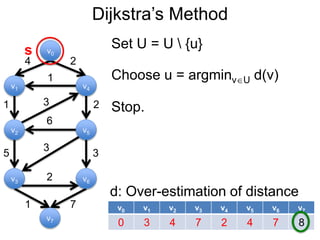
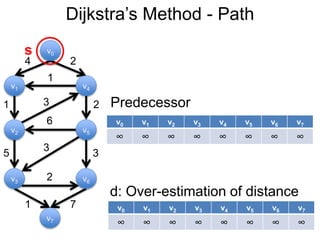
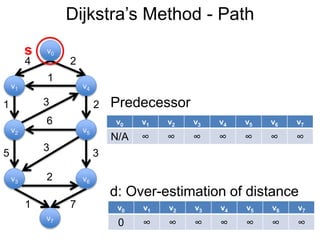
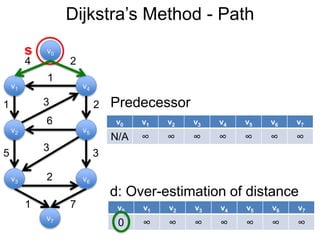
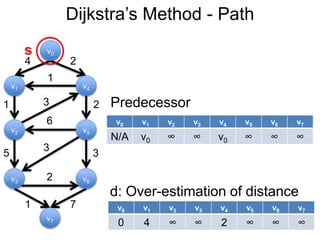
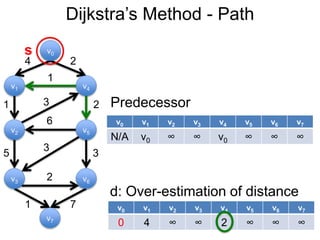
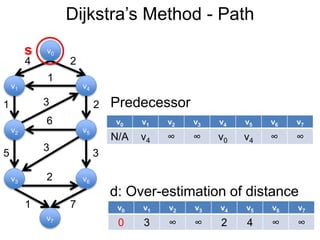
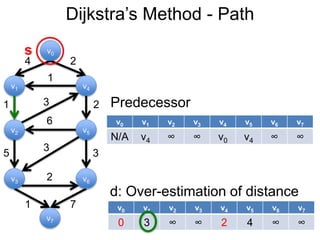
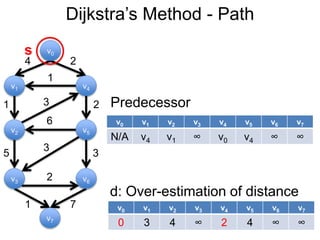
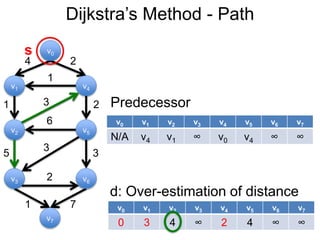
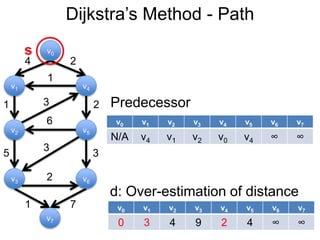
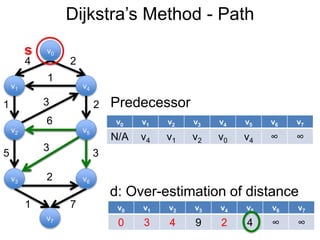
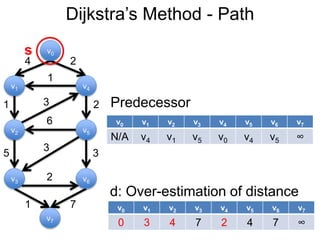
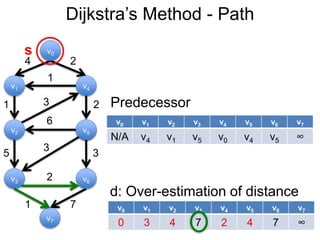
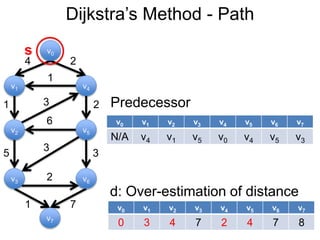
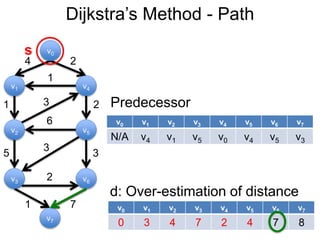
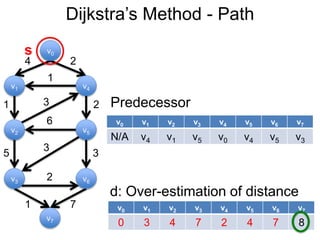
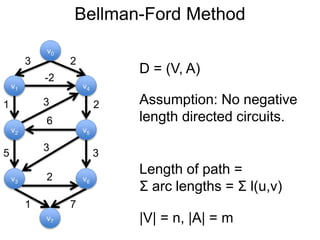
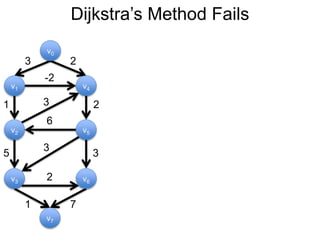
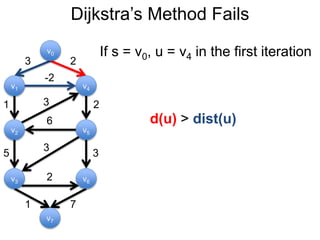
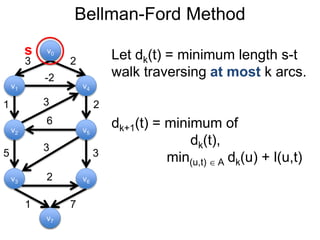
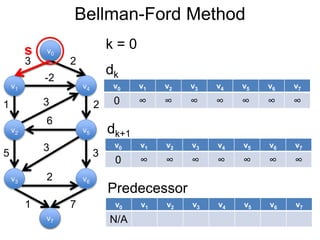
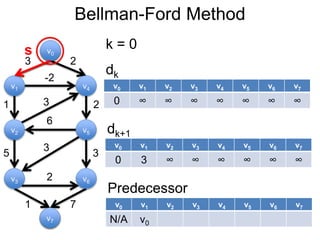
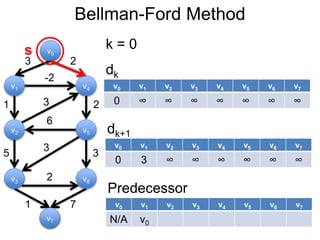
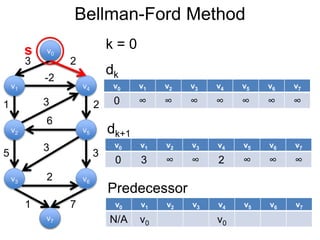
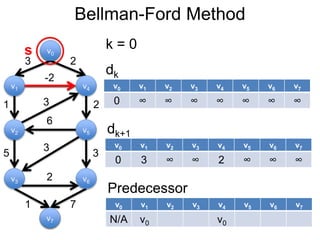
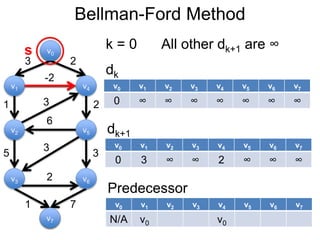
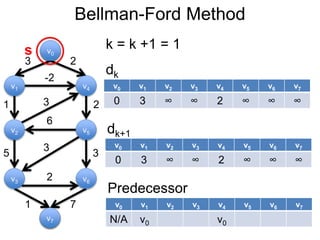
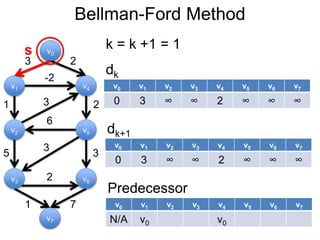
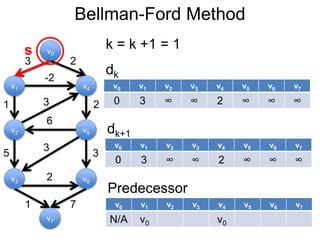
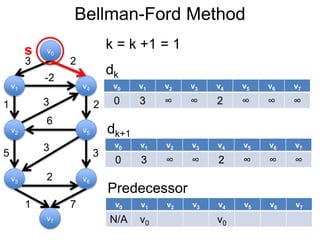
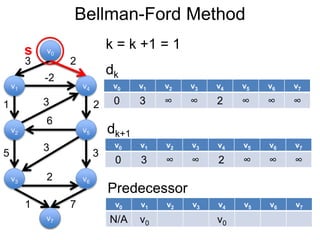
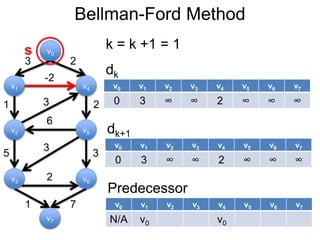
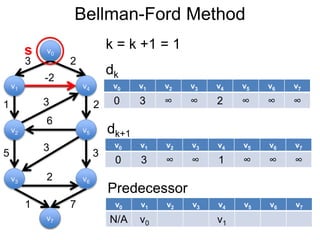
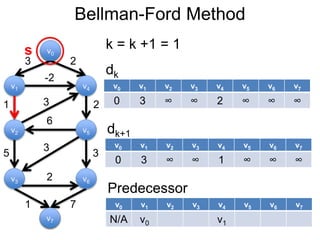
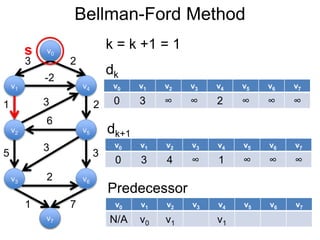
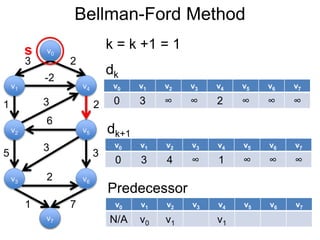
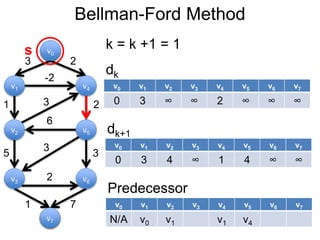
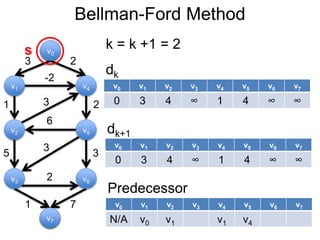
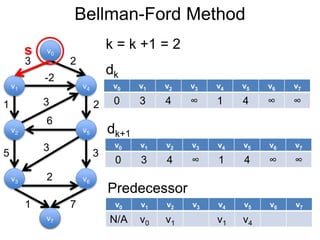
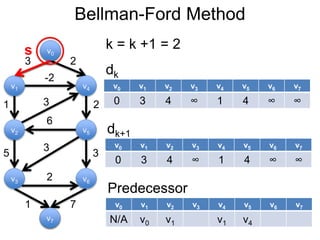
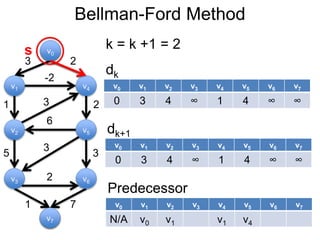
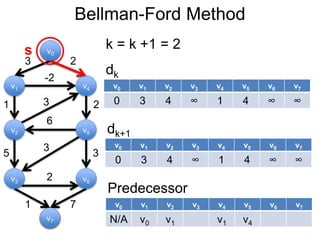
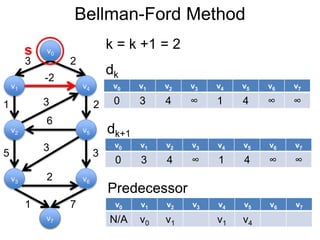
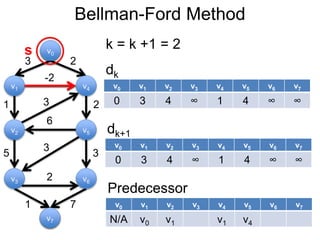
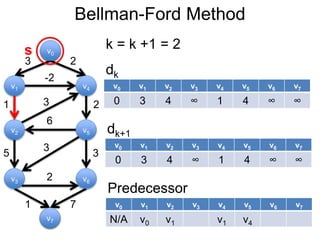
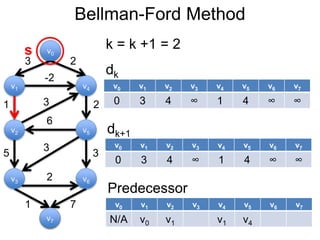
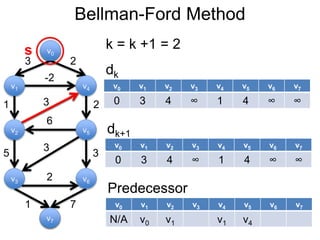
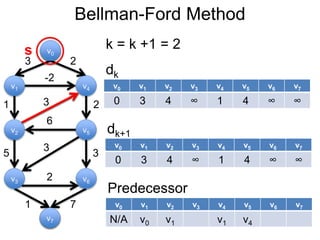
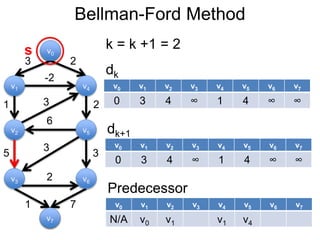
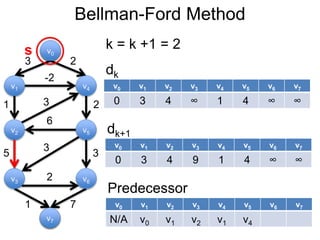
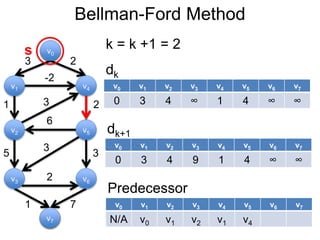
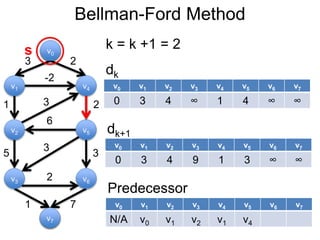
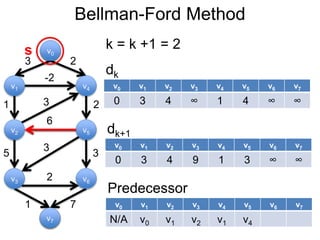
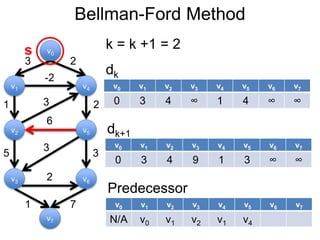
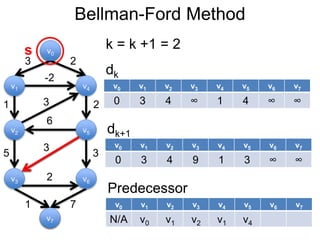
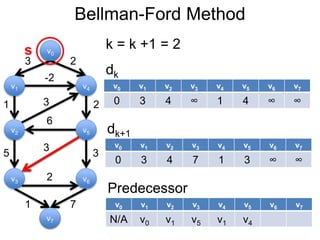
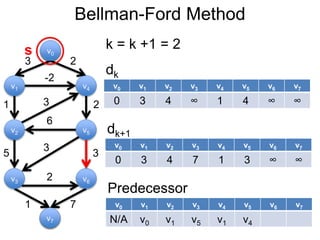
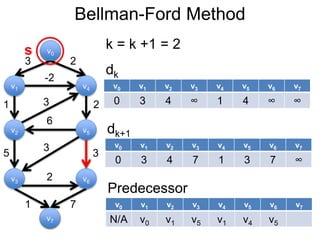
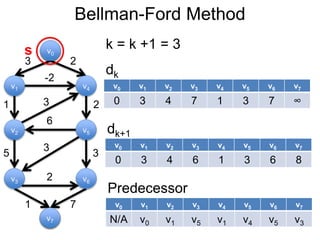
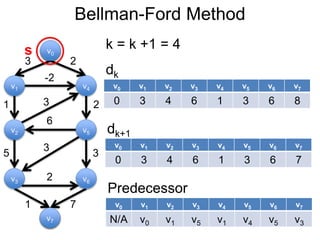
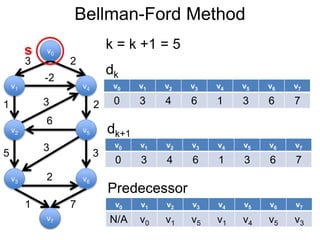
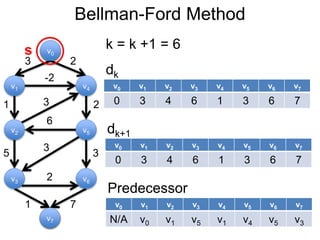
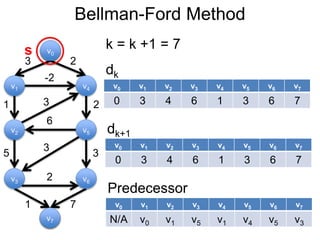
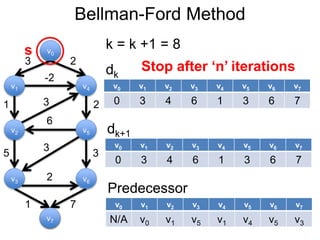
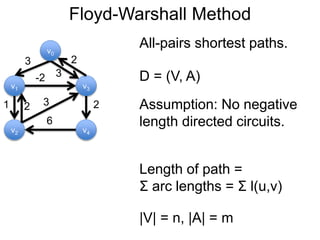
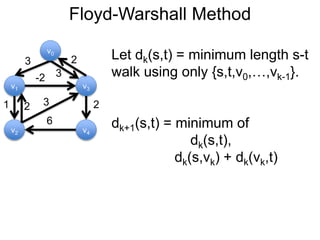
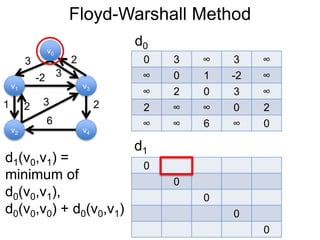
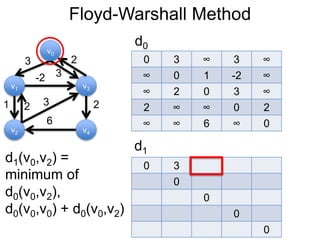
Este documento fornece um resumo de uma palestra sobre algoritmos de caminho mais curto em grafos. Ele inclui: 1) Uma introdução aos grafos direcionados e não direcionados; 2) Uma breve discussão sobre complexidade algorítmica; 3) Um esboço dos principais algoritmos de caminho mais curto, incluindo busca em largura, método de Dijkstra e método de Bellman-Ford.

1. Network Optimization
Lecture 1
Shortest paths
Mahdi Abbasi, Associate Professor
Department of Computer Engineering, Bu Ali Sina University
Email: abbasi@basu.ac.ir
Reference of this lecture slides:
Ahuja, Ravindra K., Thomas L. Magnanti, and James B. Orlin. Network
Flows: Theory, Algorithms, and Applications. Upper Saddle River, NJ:
Prentice Hall, 1993. ISBN: 9780136175490.

2. • Graph Preliminaries
– Undirected Graphs
– Directed Graphs
• Complexity Preliminaries
• Shortest Path Algorithms
Outline

3. Undirected Graphs
v1
v0
v2
v6
v4
v5
v3
‘n’ vertices or nodes V
‘m’ edges E: unordered pairs from V
G = (V, E)

4. Neighboring or Adjacent Vertices
Connected by an edge e = (u,v) = (v,u).
‘v0’ and ‘v1’ adjacent, ‘v0’ and ‘v5’ not adjacent, …
G = (V, E)
v1
v0
v2
v6
v4
v5
v3

5. Parallel Edges
Represented by the same pair of vertices.
G = (V, E)
v1
v0
v2
v6
v4
v5
v3

6. Loops
Edges that connect a vertex to itself.
G = (V, E)
v1
v0
v2
v6
v4
v5
v3

7. Simple Graphs
Graphs without parallel edges and without loops.
G = (V, E)
v1
v0
v2
v6
v4
v5
v3

8. Degree of a Vertex
Number of edges incident on the vertex.
deg(v0) = 2, deg(v1) = 2, deg(v4) = 3, …
G = (V, E)
v1
v0
v2
v6
v4
v5
v3

9. Walk
G = (V, E)
Sequence P = (v0,e1,v1,…,ek,vk), ei = (vi-1,vi)
v1
v0
v2
v6
v4
v5
v3
v0, (v0,v4), v4, (v4,v2), v2, (v2,v5), v5, (v5,v4), v4

10. Path
G = (V, E)
Sequence P = (v0,e1,v1,…,ek,vk), ei = (vi-1,vi)
v1
v0
v2
v6
v4
v5
v3
Vertices v0,v1,…,vk are distinct

11. Length of a Walk
G = (V, E)
Number of edges: k
v1
v0
v2
v6
v4
v5
v3
Length of above walk = 5

12. Length of a Walk
G = (V, E)
Sum of lengths of all edges: Σi l(ei)
v1
v0
v2
v6
v4
v5
v3
Length of above walk = 4+2+5-2+4 = 13
l: E  R
2 4
2
5
1
1
1
4
-2

13. Closed Walk
G = (V, E)
Sequence P = (v0,e1,v1,…,ek,vk), ei = (vi-1,vi)
v0 = vk
v1
v0
v2
v6
v4
v5
v3

14. Circuit
G = (V, E)
Sequence P = (v0,e1,v1,…,ek,vk), ei = (vi-1,vi)
v0 = vk
v1
v0
v2
v6
v4
v5
v3
Vertices v0,v1,…,vk-1 are distinct

15. • Graph Preliminaries
– Undirected Graphs
– Directed Graphs
• Complexity Preliminaries
• Shortest Path Algorithms
Outline

16. Directed Graphs (Digraphs)
v1
v0
v2
v6
v4
v5
v3
‘n’ vertices or nodes V
‘m’ arcs A: ordered pairs from V
D = (V, A)

17. Neighboring or Adjacent Vertices
Connected by an arc a = (u,v).
‘v0’ is the inneighbor of ‘v4’
v1
v0
v2
v6
v4
v5
v3
D = (V, A)

18. Neighboring or Adjacent Vertices
Connected by an arc a = (u,v).
‘v4’ is the outneighbor of ‘v0’
v1
v0
v2
v6
v4
v5
v3
D = (V, A)

19. Parallel Arcs
Represented by the same ordered pair of vertices.
v1
v0
v2
v6
v4
v5
v3
D = (V, A)

20. Loops
Arcs that connect a vertex to itself.
v1
v0
v2
v6
v4
v5
v3
D = (V, A)

21. Simple Graphs
Graphs without parallel arcs and without loops.
v1
v0
v2
v6
v4
v5
v3
D = (V, A)

22. Underlying Undirected Graph
Graphs obtained by ignoring orientation of arcs.
v1
v0
v2
v6
v4
v5
v3
D = (V, A)

23. Underlying Undirected Graph
Graphs obtained by ignoring orientation of arcs.
G = (V, E)
v1
v0
v2
v6
v4
v5
v3

24. Indegree of a Vertex
Number of arcs entering the vertex.
indeg(v0) = 1, indeg(v1) = 1, indeg(v4) = 2, …
D = (V, A)
v1
v0
v2
v6
v4
v5
v3

25. Outdegree of a Vertex
Number of arcs leaving the vertex.
outdeg(v0) = 1, outdeg(v1) = 1, outdeg(v2) = 2, …
D = (V, A)
v1
v0
v2
v6
v4
v5
v3

26. Walk
Sequence P = (v0,a1,v1,…,ak,vk), ai = (vi-1,vi)
v0, (v0,v4), v4, (v4,v5), v5, (v5,v2), v2, (v2,v4), v4
D = (V, A)
v1
v0
v2
v6
v4
v5
v3

27. Path
Sequence P = (v0,a1,v1,…,ak,vk), ai = (vi-1,vi)
D = (V, A)
v1
v0
v2
v6
v4
v5
v3
Vertices v0,v1,…,vk are distinct

28. Length of a Walk
D = (V, A)
v1
v0
v2
v6
v4
v5
v3
Number of arcs: k
Length of above walk = 4

29. Length of a Walk
D = (V, A)
v1
v0
v2
v6
v4
v5
v3
l: E  R
2 4
2
5
1
1
1
4
-2
Sum of lengths of all edges: Σi l(ei)
Length of above walk = 4+1+5+1 = 11

30. Closed Walk
D = (V, A)
Sequence P = (v0,a1,v1,…,ak,vk), ai = (vi-1,vi)
v0 = vk
v1
v0
v2
v6
v4
v5
v3

31. Circuit
D = (V, A)
Sequence P = (v0,a1,v1,…,ak,vk), ai = (vi-1,vi)
v0 = vk
v1
v0
v2
v6
v4
v5
v3
Vertices v0,v1,…,vk-1 are distinct

32. • Graph Preliminaries
• Complexity Preliminaries
• Shortest Path Algorithms
Outline

33. f(n)  O(g(n))
There exists k > 0 and n0 such that
f(n) ≤ k g(n)
for all n ≥ n0
f(n) = 5n2 + 3nlog(n)
g(n) = n2
f(n) = 5n3 + 3nlog(n)
g(n) = n2
✔ ✗

34. • Graph Preliminaries
• Complexity Preliminaries
• Shortest Path Algorithms
– Breadth-first Search
– Dijkstra’s Method
– Bellman-Ford Method
– Floyd-Warshall Method
Outline

35. The Shortest Path Problem
v1
v0
v2
v6
v4
v5
v3
v7
Find the shortest path from s to t
Length of path =
Number of arcs

36. The Shortest Path Problem
v1
v0
v2
v6
v4
v5
v3
v7
3 2
-1
1 2
5 -3
3
6
3
2
1 7
Find the shortest path from s to t
Length of path =
Σ Length of arcs

37. Applications
Minimize number
of stops
(lengths = 1)
Minimize amount
of time
(positive lengths)

38. Applications
Example courtesy of Robert Sedgewick
GBP EUR JPY CHF USD GOLD
GBP 1.0 0.6853 0.005290 0.4569 0.6368 208.1
EUR 1.4599 1.0 0.007721 0.6677 0.9303 304.028
JPY 189.05 129.52 1.0 85.4694 120.4 39346.7
CHF 2.1904 1.4978 0.011574 1.0 1.3941 455.2
USD 1.5714 1.0752 0.008309 0.7182 1.0 327.25
GOLD 0.004816 0.003295 0.000025
5
0.002201 0.003065 1.0
Convert 1 ounce of gold to US dollars
1 GOLD = 455.2 * 0.6677 * 1.0752 = 327.28 USD
Take log to convert products to sums
(possibly negative lengths)

39. • Graph Preliminaries
• Complexity Preliminaries
• Shortest Path Algorithms
– Breadth-first Search
– Dijkstra’s Method
– Bellman-Ford Method
– Floyd-Warshall Method
Outline

40. Breadth-First Search
v1
v0
v2
v6
v4
v5
v3
v7
Assumption: all lengths = 1
Length of path = Number of arcs
s
|V| = n, |A| = m
D = (V, A)

41. Breadth-First Search
Queue is empty. All nodes unvisited.
Push ‘s’ to queue. Set length(s) = 0.
While (‘t’ is unvisited)
Pop u from queue.
Length(unvisited outneighbors) = Length(u)+1
Push unvisited outneighbors to queue
End
Shortest path to all vertices from ‘s’

42. Breadth-First Search
v1
v0
v2
v6
v4
v5
v3
v7
s Populate the queue with ‘s’
v0 v1 v2 v3 v4 v5 v6 v7
0
v0
Queue
Length
Length of ‘s’ = 0.

43. Breadth-First Search
v1
v0
v2
v6
v4
v5
v3
v7
s Pop from the queue.
v0 v1 v2 v3 v4 v5 v6 v7
0 1 1
v1 v4
Queue
Length
u = v0
Push unvisited outneighbors to queue.
Length(unvisited outneighbors) =
Length(u) + 1

44. Breadth-First Search
v1
v0
v2
v6
v4
v5
v3
v7
s Pop from the queue.
v0 v1 v2 v3 v4 v5 v6 v7
0 1 2 1
v4 v2
Queue
Length
u = v1
Push unvisited outneighbors to queue.
Length(unvisited outneighbors) =
Length(u) + 1

45. Breadth-First Search
v1
v0
v2
v6
v4
v5
v3
v7
s Pop from the queue.
v0 v1 v2 v3 v4 v5 v6 v7
0 1 2 1 2
v2 v5
Queue
Length
u = v4
Push unvisited outneighbors to queue.
Length(unvisited outneighbors) =
Length(u) + 1

46. Breadth-First Search
v1
v0
v2
v6
v4
v5
v3
v7
s Pop from the queue.
v0 v1 v2 v3 v4 v5 v6 v7
0 1 2 3 1 2
v5 v3
Queue
Length
u = v2
Push unvisited outneighbors to queue.
Length(unvisited outneighbors) =
Length(u) + 1

47. Breadth-First Search
v1
v0
v2
v6
v4
v5
v3
v7
s Pop from the queue.
v0 v1 v2 v3 v4 v5 v6 v7
0 1 2 3 1 2 3
v3 v6
Queue
Length
u = v5
Push unvisited outneighbors to queue.
Length(unvisited outneighbors) =
Length(u) + 1

48. Breadth-First Search
v1
v0
v2
v6
v4
v5
v3
v7
s Pop from the queue.
v0 v1 v2 v3 v4 v5 v6 v7
0 1 2 3 1 2 3 4
v6
Queue
Length
Push unvisited outneighbors to queue.
u = v3
Length(unvisited outneighbors) =
Length(u) + 1

49. Breadth-First Search
Queue is empty. All nodes unvisited.
Push ‘s’ to queue. Set length(s) = 0.
While (‘t’ is unvisited)
Pop u from queue.
Length(unvisited outneighbors) = Length(u)+1
Push unvisited outneighbors to queue
End
Shortest path to all vertices from ‘s’

50. Analysis
Time Complexity : O( n + m )
Queue operations
At most ‘n’ elements in the queue
In the worst case, all arcs will be visited once

51. How fast is O( n + m )?
Complexity of this type is called linear.
Just reading the data from disk is also linear.
My laptop does 107 addition in 2 seconds
(python)
Graphs with 105 edges are tractable.

52. • Graph Preliminaries
• Complexity Preliminaries
• Shortest Path Algorithms
– Breadth-first Search
– Dijkstra’s Method
– Bellman-Ford Method
– Floyd-Warshall Method
Outline

53. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
Assumption: No negative
arc lengths
|V| = n, |A| = m
D = (V, A)
Length of path =
Σ arc lengths = Σ l(u,v)

54. Breadth-First Search Fails
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7

55. Breadth-First Search Fails
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
Counter-example !!
Blue with shorter than red.

56. Dijkstra’s Method
Set d(v) = ∞ for all v  V. Set U = V.
Set d(s) = 0. Set u = s.
Choose u = argminvU d(v)
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}
While u is not equal to t
End
Set U = U {u}

57. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = V; Set d(s) = 0
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

58. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 4 ∞ ∞ 2 ∞ ∞ ∞
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = V
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

59. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 4 ∞ ∞ 2 ∞ ∞ ∞
d: Over-estimation of distance
s Set U = U {u}

60. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 4 ∞ ∞ 2 ∞ ∞ ∞
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

61. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 4 ∞ ∞
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

62. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s Set U = U {u}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 4 ∞ ∞

63. v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 4 ∞ ∞
Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

64. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 2 4 ∞ ∞

65. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s Set U = U {u}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 2 4 ∞ ∞

66. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 2 4 ∞ ∞
Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

67. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 2 4 ∞ ∞

68. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s Set U = U {u}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 2 4 ∞ ∞

69. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 2 4 ∞ ∞
Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

70. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 ∞

71. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s Set U = U {u}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 ∞

72. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 ∞
Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

73. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8

74. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s Set U = U {u}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8

75. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8
Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}

76. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8

77. Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s Set U = U {u}
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8

78. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8
Dijkstra’s Method
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
Choose u = argminvU d(v)
Set U = U {u}
Stop.

79. Summary
Set d(v) = ∞ for all v  V. Set U = V.
Set d(s) = 0. Set u = s.
Choose u = argminvU d(v)
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}
While u is not equal to t
End
Set U = U {u}

80. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞
Predecessor

81. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A ∞ ∞ ∞ ∞ ∞ ∞ ∞
Predecessor

82. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A ∞ ∞ ∞ ∞ ∞ ∞ ∞
Predecessor

83. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 4 ∞ ∞ 2 ∞ ∞ ∞
s
d: Over-estimation of distance
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 ∞ ∞ v0 ∞ ∞ ∞
Predecessor

84. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 4 ∞ ∞ 2 ∞ ∞ ∞
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 ∞ ∞ v0 ∞ ∞ ∞
Predecessor

85. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7 v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 4 ∞ ∞
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 ∞ ∞ v0 v4 ∞ ∞
Predecessor

86. v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 4 ∞ ∞
Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 ∞ ∞ v0 v4 ∞ ∞
Predecessor

87. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 2 4 ∞ ∞
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 ∞ v0 v4 ∞ ∞
Predecessor

88. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 2 4 ∞ ∞
Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 ∞ v0 v4 ∞ ∞
Predecessor

89. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 2 4 ∞ ∞
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 v2 v0 v4 ∞ ∞
Predecessor

90. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 2 4 ∞ ∞
Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 v2 v0 v4 ∞ ∞
Predecessor

91. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 ∞
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 v5 v0 v4 v5 ∞
Predecessor

92. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 ∞
Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1
5
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 v5 v0 v4 v5 ∞
Predecessor
v5
2
3

93. Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 v5 v0 v4 v5 v3
Predecessor

94. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8
Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 v5 v0 v4 v5 v3
Predecessor

95. v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 2 4 7 8
Dijkstra’s Method - Path
v1
v0
v2
v6
v4
v5
v3
v7
4 2
1
1 2
5 3
3
6
3
2
1 7
d: Over-estimation of distance
s
v0 v1 v2 v3 v4 v5 v6 v7
N/A v4 v1 v5 v0 v4 v5 v3
Predecessor

96. Time Complexity
Maximum ‘n’ iterations
Each iteration is O(n)
Total time complexity = O(n2)
Graphs with up to 1000 nodes

97. Can we do faster?
Yes, we can do O( (n + m) log n )
We need a data structure to store d:
priority queue or heap
It allows 2 operations on elements:
1) Popping the minimum in O(log n)
2) Modifying an element in O(log n)

98. Data structure: heap
5
1
3
4
9 8
1 2 3 4 5 6
1 5 3 9 8 4
Binary tree, where each node
is smaller than its children
Minimum is always at the root
Shape: balanced tree
Binary tree can be implemented with an array:

99. Heap: adding elements
5
1
3
4 0
9 8
When adding an element
we check its parent to keep
the heap properties.

100. Heap: adding elements
5
1
0
4 3
9 8
When adding an element
we check its parent to keep
the heap properties.

101. Heap: adding elements
5
0
1
4 3
9 8
When adding an element
we check its parent to keep
the heap properties.

102. Heap: popping elements
5
3
1
4
9 8
When popping an element
we replace the root with the
last element.
We check its children to keep
the heap properties.

103. Heap: popping elements
5
1
3
4
9 8
When popping an element
we replace the root with the
last element.
We check its children to keep
the heap properties.

104. Dijkstra’s Method with heap
Set d(v) = ∞ for all v  V. Set U = V.
Set d(s) = 0. Set u = s.
Pop from heap u = argminvU d(v)
For each v such that (u,v)  A
End
d(v) = min { d(v), d(u) + l(u,v)}
While u is not equal to t
End
Set U = U {u}
Init heap
Update d(v) in the heap

105. • Graph Preliminaries
• Complexity Preliminaries
• Shortest Path Algorithms
– Breadth-first Search
– Dijkstra’s Method
– Bellman-Ford Method
– Floyd-Warshall Method
Outline

106. Bellman-Ford Method
v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Assumption: No negative
length directed circuits.
|V| = n, |A| = m
D = (V, A)
Length of path =
Σ arc lengths = Σ l(u,v)

107. Dijkstra’s Method Fails
v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7

108. Dijkstra’s Method Fails
v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
If s = v0, u = v4 in the first iteration
d(u) > dist(u)

109. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s Let dk(t) = minimum length s-t
walk traversing at most k arcs.
dk+1(t) = minimum of
dk(t),
min(u,t)  A dk(u) + l(u,t)

110. Bellman-Ford Method
k = 0. dk(s) = 0
While (k < n)
End
k = k + 1
dk+1(v) = min { dk+1(v), dk(u) + l(u,v) }
dk+1(t) = dk(t)
For each (u,v)  A
End

111. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = 0
v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
dk
v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A
Predecessor

112. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = 0
v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
dk
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ ∞ ∞ ∞ ∞
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0
Predecessor

113. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = 0
v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
dk
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ ∞ ∞ ∞ ∞
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0
Predecessor

114. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = 0
v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
dk
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor

115. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = 0
v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
dk
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor

116. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = 0
v0 v1 v2 v3 v4 v5 v6 v7
0 ∞ ∞ ∞ ∞ ∞ ∞ ∞
dk
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor
All other dk+1 are ∞

117. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor

118. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞

119. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞

120. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞

121. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞

122. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v0
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞

123. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 1 ∞ ∞ ∞

124. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 1 ∞ ∞ ∞

125. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 ∞ ∞ ∞

126. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 ∞ ∞ ∞

127. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 1
v0 v1 v2 v3 v4 v5 v6 v7
0 3 ∞ ∞ 2 ∞ ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

128. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor

129. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

130. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

131. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

132. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

133. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

134. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

135. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

136. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

137. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

138. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

139. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞

140. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v2 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 1 4 ∞ ∞

141. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v2 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 1 4 ∞ ∞

142. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v2 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 1 3 ∞ ∞

143. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v2 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 1 3 ∞ ∞

144. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v2 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 1 3 ∞ ∞

145. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v2 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 9 1 3 ∞ ∞

146. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 1 3 ∞ ∞

147. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 1 3 ∞ ∞

148. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 2
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 ∞ 1 4 ∞ ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4 v5
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 1 3 7 ∞

149. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 3
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 7 1 3 7 ∞
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4 v5 v3
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 8

150. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 4
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 8
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4 v5 v3
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7

151. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 5
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4 v5 v3
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7

152. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 6
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4 v5 v3
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7

153. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 7
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4 v5 v3
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7

154. v1
v0
v2
v6
v4
v5
v3
v7
3 2
-2
1 2
5 3
3
6
3
2
1 7
Bellman-Ford Method
v0
v7
s k = k +1 = 8
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7
dk
dk+1
v0 v1 v2 v3 v4 v5 v6 v7
N/A v0 v1 v5 v1 v4 v5 v3
Predecessor
v0 v1 v2 v3 v4 v5 v6 v7
0 3 4 6 1 3 6 7
Stop after ‘n’ iterations

155. Summary
k = 0. dk(s) = 0
While (k < n)
End
k = k + 1
dk+1(v) = min { dk+1(v), dk(u) + l(u,v) }
dk+1(t) = dk(t)
For each (u,v)  A
End

156. Time Complexity
O( n m )
Outer iteration
Run ‘n’ times
Inner Iteration
O(m) operations

157. • Graph Preliminaries
• Complexity Preliminaries
• Shortest Path Algorithms
– Breadth-first Search
– Dijkstra’s Method
– Bellman-Ford Method
– Floyd-Warshall Method
Outline

158. Floyd-Warshall Method
Assumption: No negative
length directed circuits.
|V| = n, |A| = m
D = (V, A)
Length of path =
Σ arc lengths = Σ l(u,v)
All-pairs shortest paths.
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
3
2

159. Bellman-Ford Method’s Complexity
Apply Bellman-Ford ‘n’ times
O(n2m)
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
3
2

160. Floyd-Warshall Method
Let dk(s,t) = minimum length s-t
walk using only {s,t,v0,…,vk-1}.
dk+1(s,t) = minimum of
dk(s,t),
dk(s,vk) + dk(vk,t)
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
3
2

161. Floyd-Warshall Method
k = 0. dk(i,j) = l(i,j) if (i,j)  A, otherwise ∞
While (k < n)
End
k = k + 1
dk+1(i,j) = min { dk(i,j), dk(i,vk) + dk(vk,j)}
For each i  V
End
For each j  V
End

162. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0
0
0
0
0
d1(v0,v1) =
minimum of
d0(v0,v1),
d0(v0,v0) + d0(v0,v1)

163. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3
0
0
0
0
d1(v0,v2) =
minimum of
d0(v0,v2),
d0(v0,v0) + d0(v0,v2)

164. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞
0
0
0
0
d1(v0,v3) =
minimum of
d0(v0,v3),
d0(v0,v0) + d0(v0,v3)

165. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3
0
0
0
0
d1(v0,v4) =
minimum of
d0(v0,v4),
d0(v0,v0) + d0(v0,v4)

166. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
0
0
0
0
d1(v1,v0) =
minimum of
d0(v1,v0),
d0(v1,v0) + d0(v0,v0)

167. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0
0
0
0
d1(v1,v2) =
minimum of
d0(v1,v2),
d0(v1,v0) + d0(v0,v2)

168. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1
0
0
0
d1(v1,v3) =
minimum of
d0(v1,v3),
d0(v1,v0) + d0(v0,v3)

169. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2
0
0
0
d1(v1,v4) =
minimum of
d0(v1,v4),
d0(v1,v0) + d0(v0,v4)

170. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
0
0
0
d1(v2,v0) =
minimum of
d0(v2,v0),
d0(v2,v0) + d0(v0,v0)

171. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 0
0
0
d1(v2,v1) =
minimum of
d0(v2,v1),
d0(v2,v0) + d0(v0,v1)

172. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0
0
0
d1(v2,v3) =
minimum of
d0(v2,v3),
d0(v2,v0) + d0(v0,v3)

173. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3
0
0
d1(v2,v4) =
minimum of
d0(v2,v4),
d0(v2,v0) + d0(v0,v4)

174. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
0
0
d1(v3,v0) =
minimum of
d0(v3,v0),
d0(v3,v0) + d0(v0,v0)

175. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 0
0
d1(v3,v1) =
minimum of
d0(v3,v1),
d0(v3,v0) + d0(v0,v1)

176. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 0
0
d1(v3,v2) =
minimum of
d0(v3,v2),
d0(v3,v0) + d0(v0,v2)

177. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0
0
d1(v3,v4) =
minimum of
d0(v3,v4),
d0(v3,v0) + d0(v0,v4)

178. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
0
d1(v4,v0) =
minimum of
d0(v4,v0),
d0(v4,v0) + d0(v0,v0)

179. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ 0
d1(v4,v1) =
minimum of
d0(v4,v1),
d0(v4,v0) + d0(v0,v1)

180. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 0
d1(v4,v2) =
minimum of
d0(v4,v2),
d0(v4,v0) + d0(v0,v2)

181. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 0
d1(v4,v3) =
minimum of
d0(v4,v3),
d0(v4,v0) + d0(v0,v3)

182. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 ∞ ∞ 0 2
∞ ∞ 6 ∞ 0
d0
3
2
d1
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0

183. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0
0
0
0
0
d2(v0,v1) =
minimum of
d1(v0,v1),
d1(v0,v1) + d1(v1,v0)

184. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3
0
0
0
0
d2(v0,v2) =
minimum of
d1(v0,v2),
d1(v0,v1) + d1(v1,v2)

185. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4
0
0
0
0
d2(v0,v3) =
minimum of
d1(v0,v3),
d1(v0,v1) + d1(v1,v3)

186. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1
0
0
0
0
d2(v0,v4) =
minimum of
d1(v0,v4),
d1(v0,v1) + d1(v1,v4)

187. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
0
0
0
0
d2(v1,v0) =
minimum of
d1(v1,v0),
d1(v1,v1) + d1(v1,v0)

188. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0
0
0
0
d2(v1,v2) =
minimum of
d1(v1,v2),
d1(v1,v1) + d1(v1,v2)

189. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1
0
0
0
d2(v1,v3) =
minimum of
d1(v1,v3),
d1(v1,v1) + d1(v1,v3)

190. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2
0
0
0
d2(v1,v4) =
minimum of
d1(v1,v4),
d1(v1,v1) + d1(v1,v4)

191. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
0
0
0
d2(v2,v0) =
minimum of
d1(v2,v0),
d1(v2,v1) + d1(v1,v0)

192. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 0
0
0
d2(v2,v1) =
minimum of
d1(v2,v1),
d1(v2,v1) + d1(v1,v1)

193. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0
0
0
d2(v2,v3) =
minimum of
d1(v2,v3),
d1(v2,v1) + d1(v1,v3)

194. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
0
0
d2(v3,v0) =
minimum of
d1(v3,v0),
d1(v3,v1) + d1(v1,v0)

195. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 0
0
d2(v3,v1) =
minimum of
d1(v3,v1),
d1(v3,v1) + d1(v1,v1)

196. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 0
0
d2(v3,v2) =
minimum of
d1(v3,v2),
d1(v3,v1) + d1(v1,v2)

197. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0
0
d2(v3,v4) =
minimum of
d1(v3,v4),
d1(v3,v1) + d1(v1,v4)

198. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
0
d2(v4,v0) =
minimum of
d1(v4,v0),
d1(v4,v1) + d1(v1,v0)

199. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
∞ 0
d2(v4,v1) =
minimum of
d1(v4,v1),
d1(v4,v1) + d1(v1,v1)

200. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
∞ ∞ 0
d2(v4,v2) =
minimum of
d1(v4,v2),
d1(v4,v1) + d1(v1,v2)

201. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
∞ ∞ 6 0
d2(v4,v3) =
minimum of
d1(v4,v3),
d1(v4,v1) + d1(v1,v3)

202. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 ∞ 3 ∞
∞ 0 1 -2 ∞
∞ 2 0 3 ∞
2 5 ∞ 0 2
∞ ∞ 6 ∞ 0
d1
3
2
d2
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
∞ ∞ 6 ∞ 0

203. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
∞ ∞ 6 ∞ 0
d2
3
2
d3
0
0
0
0
0

204. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
∞ ∞ 6 ∞ 0
d2
3
2
d3
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
∞ 8 6 6 0

205. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 4 1 ∞
∞ 0 1 -2 ∞
∞ 2 0 0 ∞
2 5 6 0 2
∞ 8 6 6 0
d3
3
2
d4
0 3 4 1 3
0 0 1 -2 0
2 2 0 0 2
2 5 6 0 2
8 8 6 6 0

206. Floyd-Warshall Method
v1
v0
v2
v3
v4
3 2
-2
1 2
3
6
0 3 4 1 3
0 0 1 -2 0
2 2 0 0 2
2 5 6 0 2
8 8 6 6 0
d4
3
2
d5
0 3 4 1 3
0 0 1 -2 0
2 2 0 0 2
2 5 6 0 2
8 8 6 6 0

207. Summary
k = 0. dk(i,j) = l(i,j) if (i,j)  A, otherwise ∞
While (k < n)
End
k = k + 1
dk+1(i,j) = min { dk(i,j), dk(i,vk-1) + dk(vk-1,j)}
For each i  V
End
For each j  V
End

208. Time Complexity
O( n3)
Outer iteration
Run ‘n’ times
Inner Iteration
O(n2) operations: O(1) for each pair of vertices