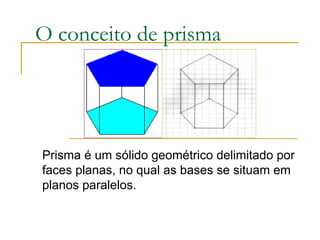
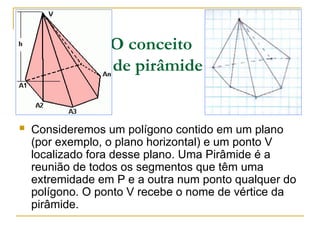
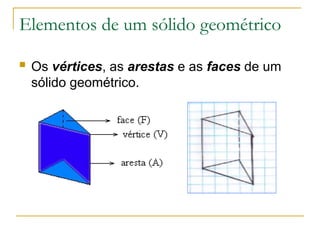
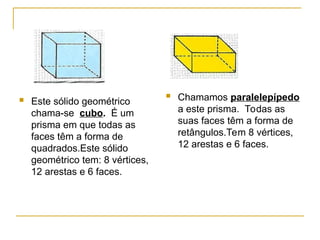
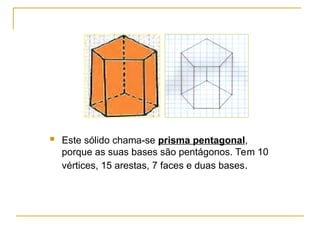
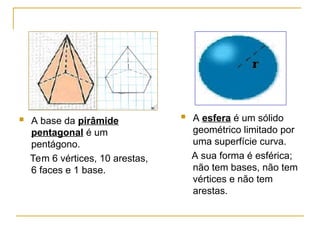
O documento aborda sólidos geométricos, como prismas e pirâmides, explicando suas características, elementos (vértices, arestas e faces) e exemplos. Também aborda o conceito de volume, apresentando a fórmula para calcular o volume de paralelepípedos e cubos, junto com exemplos práticos e exercícios. Por fim, discute diferenças e semelhanças entre diferentes sólidos, como cilindros e esferas.

1. SÓLIDOS GEOMÉTRICOS
E
VOLUMES

2. O conceito de prisma
Prisma é um sólido geométrico delimitado por
faces planas, no qual as bases se situam em
planos paralelos.

3. O conceito
de pirâmide
 Consideremos um polígono contido em um plano
(por exemplo, o plano horizontal) e um ponto V
localizado fora desse plano. Uma Pirâmide é a
reunião de todos os segmentos que têm uma
extremidade em P e a outra num ponto qualquer do
polígono. O ponto V recebe o nome de vértice da
pirâmide.
A2 A3

4. Elementos de um sólido geométrico
 Os vértices, as arestas e as faces de um
sólido geométrico.

5.  Este sólido geométrico
chama-se cubo. É um
prisma em que todas as
faces têm a forma de
quadrados.Este sólido
geométrico tem: 8 vértices,
12 arestas e 6 faces.
 Chamamos paralelepípedo
a este prisma. Todas as
suas faces têm a forma de
retângulos.Tem 8 vértices,
12 arestas e 6 faces.

6.  O prisma
quadrangular tem nas
suas bases quadrados.
Tem 8 vértices,
12 arestas, 6 faces e
2 bases.
 Este sólido geométrico
é chamado prisma
triangular porque as
suas bases são
triângulos. Tem
6 vértices, 9 arestas,
5 faces e 2 bases.

7.  Este sólido chama-se prisma pentagonal,
porque as suas bases são pentágonos. Tem 10
vértices, 15 arestas, 7 faces e duas bases.

8.  Este sólido geométrico
denomina-se pirâmide
triangular porque a sua
base é um triângulo.
Tem 4 vértices,
6 arestas, 4 faces
e 1 base.
 Chamamos pirâmide
quadrangular a este sólido
pois tem um quadrado na
sua base. Tem 5 vértices,
8 arestas, 5 faces e 1 base.

9.  A base da pirâmide
pentagonal é um
pentágono.
Tem 6 vértices, 10 arestas,
6 faces e 1 base.
 A esfera é um sólido
geométrico limitado por
uma superfície curva.
A sua forma é esférica;
não tem bases, não tem
vértices e não tem
arestas.

10.  O cone está limitado por
uma superfície curva. Tem
uma base na forma de
circunferência e tem 1
vértice.

11. Cone Cilindro Esfera
Podemos associar objetos a sólidos geométricos:

12. Volumes
 Nas construções, os engenheiros
calculam áreas para saber, por ex.,
quantos metros quadrados de
ladrilhos serão usados em
determinado ambiente. Além de
áreas, eles calculam volumes.
 Volume: é o espaço ocupado por um sólido, por
um líquido ou por gás.
 A unidade usada para se medir volume é o metro cúbico
( m³ ).
 1 m³ é o volume ocupado por um cubo de 1 metro de aresta.

13. Volume do paralelepípedo retângulo
 Vamos considerar o paralelepípedo retângulo da
figura, no qual:
c
b
a
a = comprimento
b = largura
c = altura
De modo prático, obtemos o volume do
paralelepípedo multiplicando comprimento,
largura e altura, ou seja, V = a x b x c

14. EXEMPLO
1. Uma caixa d’água tem a forma de um
paralelepípedo retângulo, com as seguintes
medidas internas: 4m , 3m e 1,5m. Qual o
volume interno dessa caixa d’água?
V = 4m x 3m x 1,5m
V = 18 m³

15. VOLUME DO CUBO
 Vamos estudar outro exemplo:
 Calcular o volume de um cubo cujas arestas
medem 4,3 m.
4,3 m
4,3 m
4,3 m V = 4,3m x 4,3m x 4,3m
V = 79,507 m³

16. EXERCÍCIOS
 1. Qual é o volume de um paralelepípedo retângulo
cujas dimensões são 30m, 18m e 12m?
 2. Determine o volume de um cubo de 2,5m de aresta.
 3. Devo construir uma piscina de 8m de comprimento
por 5m de largura e 1,5m de profundidade. Qual o
volume de terra que deve ser retirado?
 4. As dimensões de um tijolo são 0,20m de
comprimento, 0,10m de largura e 0,05m de altura. Qual
o volume de argila empregado para fabricar esse tijolo?

17.  5. Um depósito de material para construção utiliza um
caminhão basculante para transportar areia. As
dimensões internas
da carroceria do caminhão são:
comprimento = 3,40m,
largura = 2,10m e
altura = 0,80m.
Quantos metros cúbicos de
areia esse caminhão pode
carregar, no máximo?

18.  6. Calcule o volume dos seguintes sólidos geométricos:
80 cm
20 cm
20 cm
30 dm
a)
b)

19.  7. Que diferenças e semelhanças podemos observar
entre um cilindro e um prisma?
 8. Desenhe uma pirâmide de base
triangular e diga quantas faces, arestas e
vértices tem esse sólido geométrico.

20.  9. Examine os desenhos anteriores de pirâmides e
responda em seu caderno:
a) Qual é a forma das faces laterais de uma pirâmide?
b) Em que uma pirâmide é diferente de um prisma?
c) Há maior número de caixas e embalagens na forma
de prisma ou na forma de pirâmide? Por quê?
 10. Escreva uma semelhança e uma diferença entre um
cilindro e uma esfera.

21.  11. Examine os desenhos e responda:
 12. Escreva uma semelhança e uma diferença entre o cone e o cilindro.
 13. Responda:
a) Por que essa forma é chamada de prisma retangular ou
bloco retangular?
b) Quantas faces, arestas e vértices tem o bloco
retangular?
c) O que a intersecção de duas faces determina?
Qual é a diferença entre um cubo e um bloco
retangular?