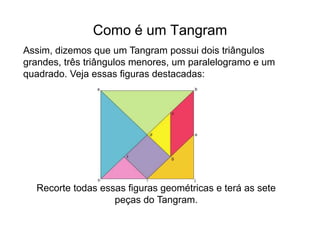
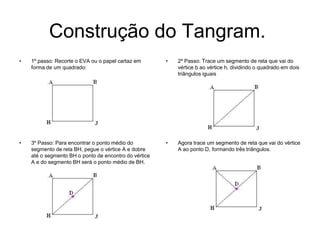
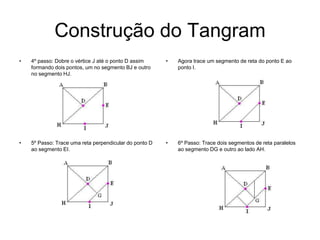
O documento descreve o jogo Tangram, incluindo sua história, como é construído e como pode ser usado no ensino fundamental para trabalhar conceitos matemáticos como formas geométricas e frações. Ele também detalha um software educacional de Tangram e atividades que podem ser realizadas com as crianças usando o software.

1. PEDAGOGIAPROJETO INTERDISCIPLINARENSINO DA MATEMÁTICAAVM- FACULDADE INTEGRADA

2. COMPONENTES DO GRUPOEdviges da Paixão Zoel de Assumpção Ione da Silva Gomes Ferreira Marcos DinizPasqualina Miceli Toscano Valewska da Silva BarretoProf: Heitos AchillesPedagogia – 4º período

3. TANGRAMÉ um jogo muito utilizado pelos professores de matemática para apresentar, aos alunos da educação infantil e do ensino fundamental (até o 6º ano), formas geométricas, trabalhar a lógica e a criatividade, retas, seguimentos de retas, pontos e vértices. O Software educacional TANGRAM foi projetado e desenvolvido com uma interface de fácil utilização, interativa, onde o usuário possa ter uma participação ativa, podendo, visualizar, verificar, validar mudanças e alterações ocorridas, levando o aluno a construir o conhecimento. Seu desenvolvimento foi feito utilizando o software Director versão 8.5 (Bizzoto, 2002),

4. HISTÓRIA DO TANGRAMQuando surgiu, de onde veio, quem inventou, são dúvidas que nunca foram esclarecidas sobre esse jogo. Existem inúmeras ledas sobre a história do Tangram. Dentre elas a mais comentada é que: um monge chinês deu uma tarefa a seu discípulo, pediu que ele fosse percorrer o mundo em busca de ver e relatar todas as belezas do mundo, assim deu para ele um quadrado de porcelana e vários outros objetos, para que pudesse registrar o que encontrasse. Muito descuidado deixou a porcelana cair, essa se dividiu em 7 pedaços em forma de quadrado, paralelogramo e triângulo. Com essas peças ele notou que poderia construir todas as maravilhas do mundo

5. Assim, dizemos que um Tangram possui dois triângulos grandes, três triângulos menores, um paralelogramo e um quadrado. Veja essas figuras destacadas: Recorte todas essas figuras geométricas e terá as sete peças do Tangram.Como é um Tangram

6. Construção do Tangram. 2º Passo: Trace um segmento de reta que vai do vértice b ao vértice h, dividindo o quadrado em dois triângulos iguais3º Passo: Para encontrar o ponto médio do segmento de reta BH, pegue o vértice A e dobre até o segmento BH o ponto de encontro do vértice A e do segmento BH será o ponto médio de BH.Agora trace um segmento de reta que vai do vértice A ao ponto D, formando três triângulos. 1º passo: Recorte o EVA ou o papel cartaz em forma de um quadrado:

7. Construção do Tangram4º passo: Dobre o vértice J até o ponto D assim formando dois pontos, um no segmento BJ e outro no segmento HJ. Agora trace um segmento de reta do ponto E ao ponto I.5º Passo: Trace uma reta perpendicular do ponto D ao segmento EI. 6º Passo: Trace dois segmentos de reta paralelos ao segmento DG e outro ao lado AH.

8. USO DO TANGRAM NO ENSINO FUNDAMENTAL I Este quebra-cabeça tem sido utilizado como material didático nas aulas de Artes e está cada vez mais presente nas de Matemática. Ele permite o desenvolvimento de algumas habilidades importantes para a aquisição de conhecimento s em outras áreas tais como:visualização / diferenciaçãopercepção espacial,análise / síntesedesenho, relação espacial escrita e construção

9. O que podemos abordar com o Tangram? Com o uso do tangram o professor pode trabalhar:identificação, comparação,descrição,classificação,desenho de formas geométricas planas,visualização e representação de figuras planas,exploração de transformações geométricas através de decomposição e composição de figuras,compreensão das propriedades das figuras geométricas planas, representação e resolução de problemas usando modelos geométricos noções de áreasfrações

10. Atividades com o software do TangramLevar as crianças ao laboratório de informática e contar a estória de uma menina que era uma quadrado e se desdobrava em diversas formas que ela imaginava como pássaros, pessoas, animais, casas e etc.Após contar a estória será lançado um desafio onde as crianças deverão criar imagens diversas de acordo com a sua criatividade, utilizando as peças do Tangram através do software. Elas ficarão livres para soltar a sua imaginação.No final todos deverão compartilhar sua figura com os amigos e com o professor

11. SITES CONSULTADOShttp://brincandocomtangram2.blogspot.comhttp://www.fsa.br/santoandre/upload/arquivo/Plano2009-_%20Tecnologias%20e%20Laborat%C3%B3rio%20de%20Ensino%20de%20Matem%C3%A1tica%20_.pdfhttp://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=237http://www.psicopedagogia.com.br/artigos/artigo.asp?entrID=907http://geotangram.blogspot.com/http://www.colegiocetec.com.br/cetec/images