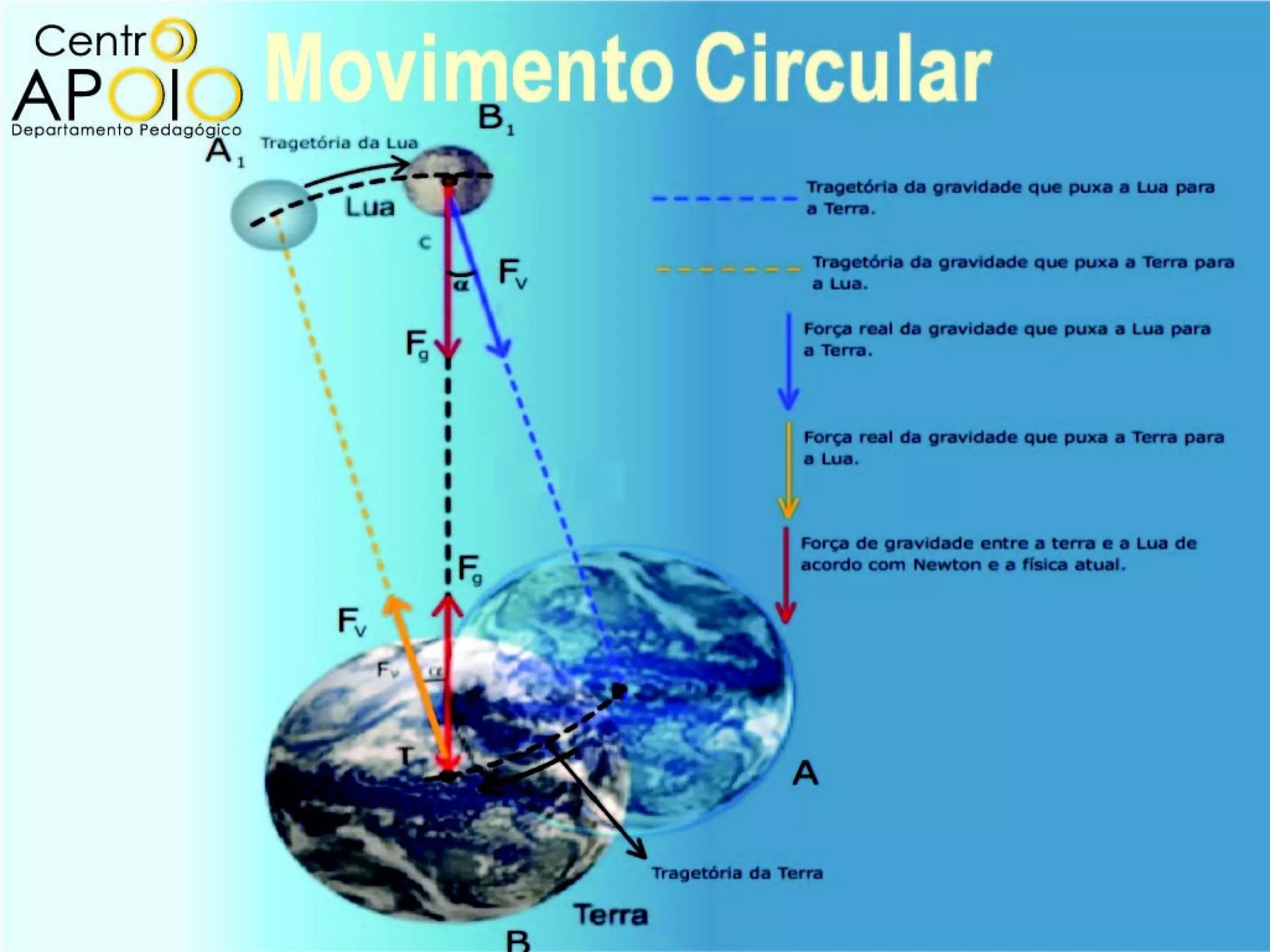
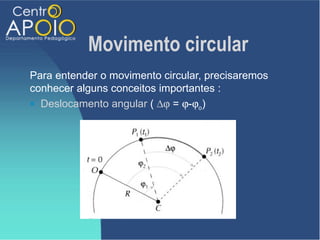
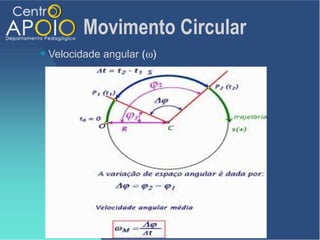
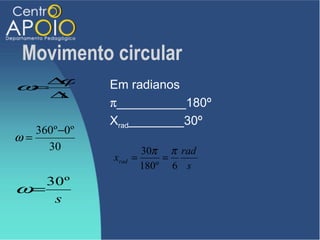
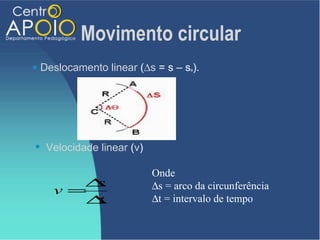
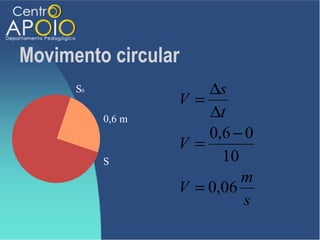
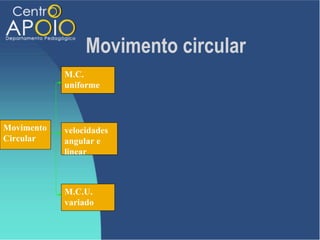
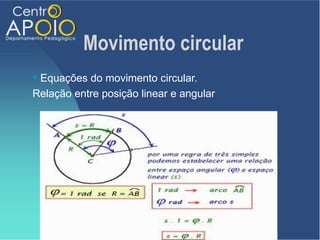
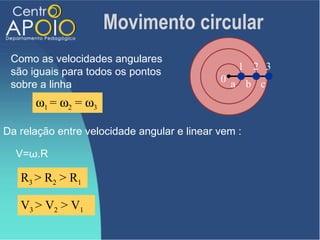
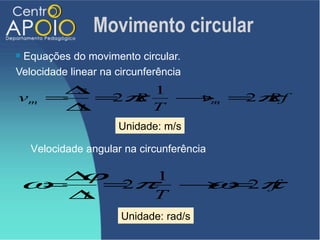
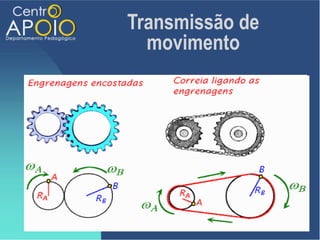
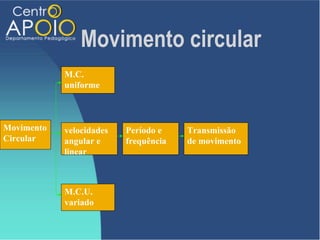
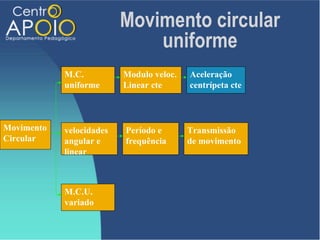
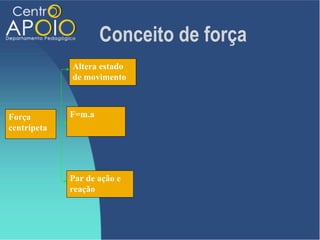
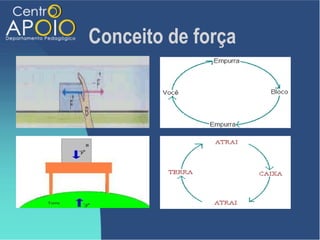
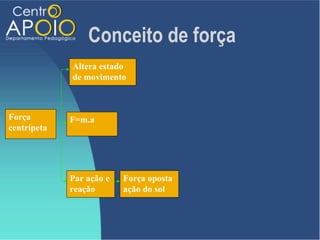
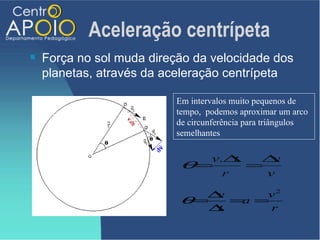
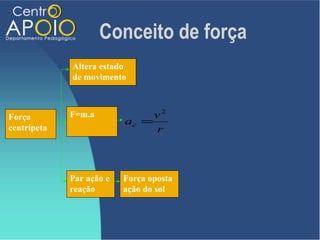
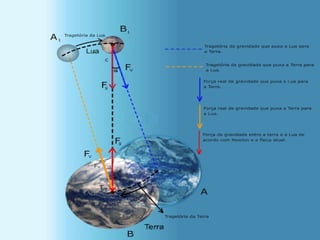
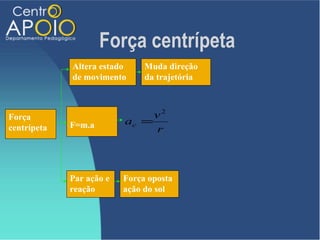
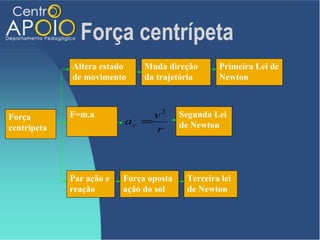
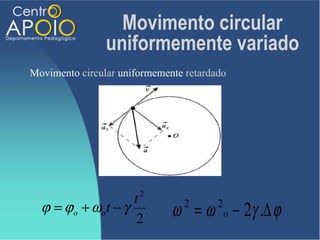
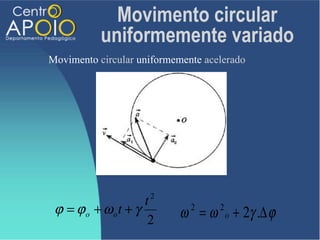
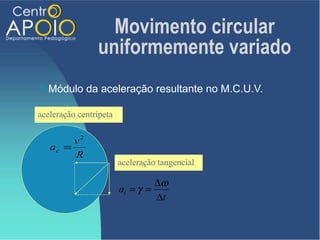
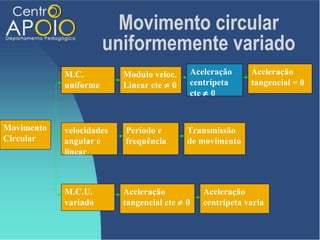
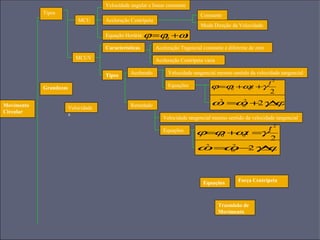
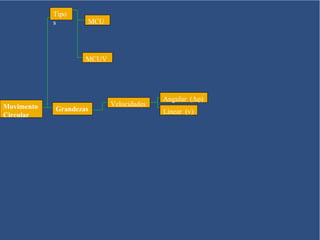
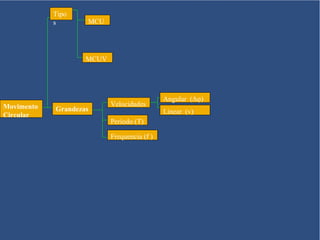
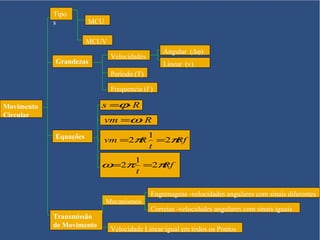
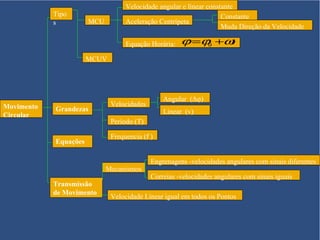
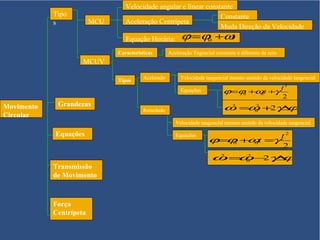
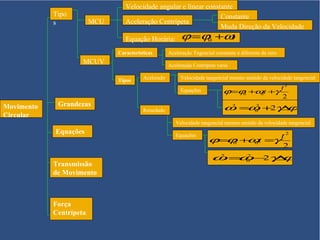
O documento aborda o movimento circular, explicando suas definições e classificações, como movimento circular uniforme (MCU) e movimento circular uniformemente variado (MCUV). Ele detalha conceitos como deslocamento angular, velocidade angular, e força centrípeta, além de apresentar equações relacionadas e exemplos práticos. As leis de Newton também são mencionadas em relação à aceleração centrípeta e suas aplicações em diferentes contextos de movimento circular.

2. Movimento Circular
Se define movimento circular como aquele cuja
trajetória é uma circunferência. Eles são
classificados como:
• Movimento circular uniforme (MCU)
•Movimento circular uniformemente variado
(MCUV)

3. Movimento Circular
M.C.
uniforme
Movimento
Circular
M.C.U.
variado

4. Movimento circular
Para entender o movimento circular, precisaremos
conhecer alguns conceitos importantes :
 Deslocamento angular ( ∆ϕ = ϕ-ϕ )
o

5. Movimento Circular
 Velocidade angular (ω)

6. Movimento circular
 Exercício
Uma roda gigante, está na posição ϕo= 0º ela faz
uma rotação e para na posição ϕ=360º, num
intervalo de 30 s.
Qual é a sua velocidade angular média?

7. Movimento circular
 Exercício
Uma roda gigante, está na posição ϕo= 0º ela faz
uma rotação e para na posição ϕ = 360º, num
intervalo de 30 s.
Qual é a sua velocidade angular média ?

8. Movimento circular
ω ∆
=
ϕ Em radianos
∆t
π__________180º
Xrad________30º
360º −0º
ω=
30 30π π rad
xrad = =
180º 6 s
30º
ω=
s

9. Movimento circular
 Deslocamento linear (∆s = s – sº).
 Velocidade linear (v)
Onde
∆s ∆s = arco da circunferência
v =
∆t ∆t = intervalo de tempo

10. Movimento circular
 Exercício
Um ponto P num disco está em sua posição So = 0
m, após 10 s, ele percorre um arco de circunferência
ficando na posição S = 0,6 m. Calcule sua velocidade
linear média nesta trajetória.

11. Movimento circular
 Exercício
Um ponto P num disco está em sua posição So = 0
m, após 10 s, ele percorre um arco de circunferência
ficando na posição S = 0,6 m. Calcule sua velocidade
linear média nesta trajetória.

12. Movimento circular
S0 ∆s
V=
0,6 m ∆t
0,6 − 0
V=
S 10
m
V = 0,06
s

13. Movimento circular
M.C.
uniforme
Movimento velocidades
Circular angular e
linear
M.C.U.
variado

14. Movimento circular
 Período (T)
É o tempo gasto para dar uma volta numa
circunferência.
 Frequência (f)
É o número de voltas (n)dado pela circunferência
por unidade de tempo (∆t).
Onde
n 1 n = número de voltas
f = = ∆t = intervalo de tempo
∆ t T
Quando n=1 , ∆t =T

15. Movimento circular
 Exercício
Uma pessoa está em uma roda-gigante que tem raio de
e gira em rotação uniforme. A pessoa passa pelo ponto
mais próximo do chão a cada 20 segundos. Podemos
afirmar que a frequência do movimento dessa pessoa,
em rpm, (rotações por minuto) é:

16. Movimento circular
 Exercício
Uma pessoa está em uma roda-gigante que gira em
rotação uniforme. A pessoa passa pelo ponto mais
próximo do chão a cada 20 segundos. Podemos afirmar
que a frequência do movimento dessa pessoa, em rpm,
(rotações por minuto) é:

17. Movimento circular
1volta
f = 20 x = 60.1
20 s
1__________20 s 60
x= = 3 rpm
x__________60s 20
Ou pela aplicação da formula de frequência
1 n
=
20 60
n =3rpm

18. Movimento circular
M.C.
uniforme
Movimento velocidades Período e
Circular angular e frequência
linear
M.C.U.
variado

19. Movimento circular
 Definição de radiano:
Um radiano é a medida do ângulo central φ que
determina, na circunferência, um arco de comprimento
igual ao raio R (s=R)

20. Movimento circular
Equações do movimento circular.
Relação entre posição linear e angular

21. Movimento circular
 Equações do movimento circular.
Relação entre velocidade angular e linear.
Dividindo os dois membros da equação anterior pelo tempo
fica:
∆ s ∆ϕ
= .R
∆ t ∆t
ω
v m = .R

22. Movimento circular
 Exercícios
Na figura, 1, 2 e 3 são partículas de massa m. A partícula 1
está presa ao ponto O pelo fio a. As partículas 2 e 3 estão
presas, respectivamente, à partícula 1 e à partícula 2, pelos
fios b e c. Todos os fios são inextensíveis e de massa
desprezível. Cada partícula realiza um movimento com
velocidade constante e centro em O. Classifique as
velocidades angulares e lineares nos três pontos quanto ao
seus módulos (maior, menor, ou igual).

23. Movimento circular
Na figura, 1, 2 e 3 são partículas de massa m. A partícula 1
está presa ao ponto O pelo fio a. As partículas 2 e 3 estão
presas, respectivamente, à partícula 1 e à partícula 2, pelos
fios b e c. Todos os fios são inextensíveis e de massa
desprezível. Cada partícula realiza um movimento com
velocidade constante e centro em O. Classifique as
velocidades angulares e lineares nos três pontos quanto ao
seus módulos (maior, menor, ou igual).

24. Movimento circular
Como as velocidades angulares
são iguais para todos os pontos 1 2 3
0 a b c
sobre a linha
ω1 = ω2 = ω3
Da relação entre velocidade angular e linear vem :
V=ω.R
R3 > R2 > R1
V3 > V2 > V1

25. Movimento circular
Equações do movimento circular.
Velocidade linear na circunferência
∆s 1
vm = =π
2 R → =π
vm 2 Rf
∆t T
Unidade: m/s
Velocidade angular na circunferência
ω=
∆ϕ= π1 → = π
2 ω 2 f
∆t T
Unidade: rad/s

26. Transmissão de
movimento
26

27. Transmissão de
movimento
 A velocidade linear nas engrenagens é a mesma em todos os
pontos
 A velocidade linear na correia é a mesma em todos os pontos.

28. Transmissão de movimento
Uma cinta funciona solidária com dois cilindros
de raios RA=10cm e RB=50cm. Supondo que o
cilindro maior tenha uma frequência de rotação fB
igual a 60rpm:
a) Qual a frequência de rotação fA do cilindro
menor?
b) Qual a velocidade linear da cinta ?

29. Transmissão de movimento
Uma cinta funciona solidária com dois cilindros
de raios RA=10cm e RB=50cm. Supondo que o
cilindro maior tenha uma frequência de rotação
fB igual a 50rpm:
a) Qual a frequência de rotação fA do cilindro
menor?
b) Qual a velocidade linear da cinta ?

30. Transmissão de movimento
a) f A .R A = f B .RB b) VA = 2πf A
f A .10 =60.50
VA = 6,28.10.300
60.50
fA = cm
10
VA = 18800
fA =300rpm s

31. Movimento circular
M.C.
uniforme
Movimento velocidades Período e Transmissão
Circular angular e frequência de movimento
linear
M.C.U.
variado

32. Movimento circular uniforme
Além de ter as características do movimento circular o
M.C.U. possui:
 A velocidade de sua trajetória constante
 Aceleração centrípeta

33. Movimento circular uniforme
A aceleração centrípeta existe por que a velocidade
linear muda constantemente de direção, apesar de seu
módulo ser constante.

34. Movimento circular uniforme
 Exemplos de movimento circular uniforme

35. Movimento circular
uniforme
 Equação horária do M.C.U.
ω cte
=
ϕ ϕ+ t
= o ω
Onde
ω = velocidade angular constante
ϕ = posição angular

36. Movimento circular
uniforme
M.C. Modulo veloc. Aceleração
uniforme Linear cte centrípeta cte
Movimento velocidades Período e Transmissão
Circular angular e frequência de movimento
linear
M.C.U.
variado

37. Conceito de força
 1a Lei de Newton: Inércia
“Todo corpo continua em seu estado de repouso ou
de movimento uniforme em uma linha reta, a
menos que seja forçado a mudar aquele estado
por forças aplicadas sobre ele”.

38. Conceito de força
 1a Lei de Newton: Inércia
“Todo corpo continua em seu estado de repouso ou
de movimento uniforme em uma linha reta, a
menos que seja forçado a mudar aquele estado
por forças aplicadas sobre ele”.

39. Conceito de força
Altera estado
de movimento
Força
centrípeta

40. Conceito de força
O menino tende a manter o estado anterior de movimento, mesmo depois do
cavalo frear. Como estão soltos, o menino acaba sendo arremessado.

41. Conceito de força
 2a Lei de Newton: F = m.a
“A mudança de movimento é proporcional à força
motora imprimida, e é produzida na direção de
linha reta na qual aquela força é imprimida.”

42. Conceito de força
 2a Lei de Newton: F = m.a
“A mudança de movimento é proporcional à força
motora imprimida, e é produzida na direção de
linha reta na qual aquela força é imprimida.”

43. Conceito de força
No caso abaixo as forças aplicadas estão na mesma
direção e sentido e tem mesmo módulo, essas forças
produzem acelerações diretamente proporcionais na
sua mesma direção e sentido.

44. Conceito de força
Altera estado
de movimento
Força
centrípeta F= m.a

45. Conceito de força
 3a Lei de Newton: pares de ação e reação
“A toda ação há sempre uma reação oposta e de
igual intensidade, ou, as ações mútuas de 2
corpos um sobre o outro são sempre iguais e
dirigidas a partes opostas"

46. Conceito de força
 3a Lei de Newton: pares de ação e reação
“A toda ação há sempre uma reação oposta e de
igual intensidade, ou, as ações mútuas de 2
corpos um sobre o outro são sempre iguais e
dirigidas a partes opostas"

47. Conceito de força
Altera estado
de movimento
Força F=m.a
centrípeta
Par de ação e
reação

48. Conceito de força
3a Lei de Newton: pares de ação e reação são :
 Forças simultâneas
Que podem ser :
 Forças de campo ou de contato

49. Conceito de força

50. Conceito de força
Altera estado
de movimento
Força F=m.a
centrípeta
Par ação e Força oposta
reação ação do sol

51. Aceleração centrípeta
 Força no sol muda direção da velocidade dos
planetas, através da aceleração centrípeta
Em intervalos muito pequenos de
tempo, podemos aproximar um arco
de circunferência para triângulos
semelhantes
θ=v.∆t
=
∆ v
r v
∆ v v2
θ= = =
a
∆t r

52. Conceito de força
Altera estado
de movimento
Força F=m.a v2
ac =
centrípeta r
Par ação e Força oposta
reação ação do sol

53. Força centrípeta
53

54. Força centrípeta
Altera estado Muda direção
de movimento da trajetória
Força v2
F=m.a ac =
centrípeta r
Par ação e Força oposta
reação ação do sol

55. Força centrípeta
 As 3 leis de Newton e a força centrípeta :
O sol atrai a terra e a terra atrai o sol, como o
sol tem maior massa, a terra que é puxada,
não cai no sol por que gira, mudando de
direção a cada momento provocando uma
força que equilibra, essa é a força centrípeta.

56. Força centrípeta
Altera estado Muda direção Primeira Lei de
de movimento da trajetória Newton
Força F=m.a v2 Segunda Lei
ac = de Newton
centrípeta r
Par ação e Força oposta Terceira lei
reação ação do sol de Newton

57. Força centrípeta
Aplicando a aceleração centrípeta na segunda lei de
Newton :
2
v
F =m.
r

58. Estrutura da apresentação
Altera estado Muda direção Primeira Lei de
de movimento da trajetória Newton
Força F=m.a v2 Segunda Lei v2
ac = de Newton F =m.
centrípeta r r
Par ação e Força oposta Terceira lei
reação ação do sol de Newton

59. Exercícios
Um carro de massa 1,0 x 103 kg com velocidade
de 20 m/s descreve no plano horizontal uma curva
de raio 200 m. A força centrípeta e o coeficiente de
atrito tem módulos:

60. Exercícios
Um carro de massa 1,0 x 103 kg com velocidade
de 20 m/s descreve no plano horizontal uma curva
de raio 200 m. A força centrípeta e o coeficiente de
atrito tem módulos:

61. Força centrípeta
A)
Fc= m.v2 / R
Fc= 1,0 x 103 . (20)2 / 200
Fc= 2000 N
B)
Fat = Fc Fat = µN = µmg
2000 = µmg
2000 = µ.1000. 10

62. Movimento circular
uniformemente variado
Características:
 Possui aceleração tangencial constante (γ)
 A velocidade em sua trajetória varia de forma
uniforme.
ω 0
ω ≠ω
0
ω

63. Movimento circular
uniformemente variado
M.C. Modulo veloc. Aceleração Aceleração
uniforme Linear cte ≠ 0 centrípeta tangencial
cte ≠ 0 cte = 0
Movimento velocidades Período e Transmissão
Circular angular e frequência de movimento
linear
M.C.U. Aceleração
variado tangencial cte ≠ 0

64. Movimento circular
uniformemente variado
Movimento circular uniformemente retardado
2
t
ϕ = ϕ o + ωo t − γ
2
ω = ω o − 2γ .∆ ϕ
2 2

65. Movimento circular
uniformemente variado
Movimento circular uniformemente acelerado
2
t
ϕ = ϕ o + ωot + γ ω = ω o + 2γ .∆ ϕ
2 2
2

66. Movimento circular
uniformemente variado
 Módulo da aceleração resultante no M.C.U.V.
aceleração centrípeta
v2
ac =
R
aceleração tangencial
∆ω
at = γ =
∆t

67. Movimento circular
uniformemente variado
 Módulo da aceleração resultante no M.C.U.V.
Onde ar = aceleração resultante
a r=a c+a
2 2 2
t

68. Movimento circular
uniformemente variado
M.C. Modulo veloc. Aceleração Aceleração
uniforme Linear cte ≠ 0 centrípeta tangencial = 0
cte ≠ 0
Movimento velocidades Período e Transmissão
Circular angular e frequência de movimento
linear
M.C.U. Aceleração Aceleração
variado tangencial cte ≠ 0 centrípeta varia

69. Velocidade angular e linear constante
Tipos Constante
MCU Aceleração Centrípeta
Muda Direção da Velocidade
Equação Horária: ϕ =ϕ0 +ωt
Características Aceleração Tngencial constante e diferente de zero
MCUV Aceleração Centrípeta varia
Tipos Acelerado Velocidade tangencial mesmo sentido da velocidade tangencial
t2
Grandezas Equações ϕ =ϕ +ω t +γ
0 0
2
Movimento Retardado ω =ω +2γ ϕ
2 2
0 ∆
Velocidade
Circular s
Velocidade tangencial mesmo sentido da velocidade tangencial
t2
Equações
ϕ= 0 + 0t =γ
ϕ ω
2
ω= 0 −γ ϕ
2
ω 2 ∆
2
Equações Força Centrípeta
Trasmisão de
Movimento

70. Tipo
s MCU
MCUV
Movimento
Circular

71. Tipo
s MCU
MCUV
Angular (Δφ)
Movimento Velocidades
Grandezas Linear (v)
Circular

72. Tipo
s MCU
MCUV
Angular (Δφ)
Movimento Velocidades
Grandezas Linear (v)
Circular
Período (T)
Frequencia (f )

73. Tipo
s MCU
MCUV
Angular (Δφ)
Velocidades
Grandezas Linear (v)
Período (T)
Frequencia (f )
Movimento s =ϕ⋅ R
Circular
vm =ω⋅ R
Equações 1
vm =2πR =2πRf
t
1
ω=2π =2πRf
t
Engrenagens -velocidades angulares com sinais diferentes
Mecanismos
Correias -velocidades angulares com sinais iguais
Transmissão
de Movimento
Velocidade Linear igual em todos os Pontos

74. Velocidade angular e linear constante
Tipo Constante
s MCU Aceleração Centrípeta
Muda Direção da Velocidade
Equação Horária: ϕ =ϕ0 +ωt
MCUV
Angular (Δφ)
Movimento Velocidades
Grandezas Linear (v)
Circular
Período (T)
Frequencia (f )
Equações
Engrenagens -velocidades angulares com sinais diferentes
Mecanismos
Correias -velocidades angulares com sinais iguais
Transmissão
de Movimento
Velocidade Linear igual em todos os Pontos

75. Velocidade angular e linear constante
Tipo Constante
s MCU Aceleração Centrípeta
Muda Direção da Velocidade
Equação Horária: ϕ =ϕ0 +ωt
MCUV
Angular (Δφ)
Velocidades
Grandezas Linear (v)
Período (T)
Movimento Equações Frequencia (f )
Circular
Engrenagens -velocidades angulares com sinais diferentes
Mecanismos
Correias -velocidades angulares com sinais iguais
Transmissão
de Movimento
Velocidade Linear igual em todos os Pontos
Depende das Leis de Newton
Altera o estado de movimento
Fórmula: mv 2
Fc =
Força R
Centrípeta
Gera Aceleração Centrípeta – Formula: v2
ac =
R

76. Velocidade angular e linear constante
Tipo Constante
s MCU Aceleração Centrípeta
Muda Direção da Velocidade
Equação Horária: ϕ =ϕ0 +ωt
Características Aceleração Tngencial constante e diferente de zero
MCUV
Tipos Acelerado Velocidade tangencial mesmo sentido da velocidade tangencial
t2
Equações ϕ =ϕ +ω t +γ
0 0
2
Grandezas
Movimento Retardado ω =ω +2γ ϕ
2 2
0 ∆
Circular
Velocidade tangencial mesmo sentido da velocidade tangencial
Equações Equações t2
ϕ= 0 + 0t =γ
ϕ ω
2
ω= 0 −γ ϕ
2
ω 2 ∆
2
Transmissão
de Movimento
Força
Centrípeta

77. Velocidade angular e linear constante
Tipo Constante
s MCU Aceleração Centrípeta
Muda Direção da Velocidade
Equação Horária: ϕ =ϕ0 +ωt
Características Aceleração Tngencial constante e diferente de zero
MCUV Aceleração Centrípeta varia
Tipos Acelerado Velocidade tangencial mesmo sentido da velocidade tangencial
t2
Equações ϕ =ϕ +ω t +γ
0 0
2
Grandezas
Movimento Retardado ω =ω +2γ ϕ
2 2
0 ∆
Circular
Velocidade tangencial mesmo sentido da velocidade tangencial
Equações Equações t2
ϕ= 0 + 0t =γ
ϕ ω
2
ω= 0 −γ ϕ
2
ω 2 ∆
2
Transmissão
de Movimento
Força
Centrípeta

78. Lembrando
a Geometria
2π rad = 360º
Comprimento da Circunferência
C= π
2 R

79. Conceito de Força
•1ª Lei de Newton: Inércia
•2ª Lei de Newton: F = m.a
•3ª Lei de Newton: Ação e Reação