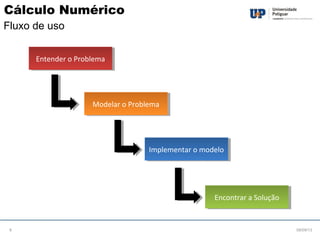
O documento apresenta uma introdução ao Cálculo Numérico, descrevendo-o como um conjunto de métodos para obter soluções aproximadas de problemas matemáticos complexos. Explica que é usado quando soluções analíticas não existem ou são difíceis de serem obtidas, e fornece exemplos de aplicações como sistemas de equações e equações diferenciais.

1. Cálculo Numérico
Apresentação e motivações
Kleber Jacinto
Eng Eletricista – Esp Em Informática – Msc Ciência da Computação
08/09/131

2. O Cálculo Numérico corresponde a um conjunto de
ferramentas ou métodos usados para se obter a
solução de problemas matemáticos.
Esses métodos são principalmente aplicados a problemas
cuja solução analítica ou algébrica é complexa ou
inexiste.
Estes métodos normalmente conduzem a soluções
aproximadas ou que possuem algum erro associado.
.
08/09/132
Cálculo Numérico
Apresentação

3. São utilizados para solução de problemas que tem soluções
exatas e analíticas mas que quando aumentam de
escala tornam-se difíceis ou impossíveis de serem
solucionados:
Ex: Sistemas de equações lineares
08/09/133
Cálculo Numérico
Aplicações

4. Também são úteis com problemas para os quais não
existem métodos matemáticos para solução (não
podem ser resolvidos analiticamente).
Ex:
• não tem primitiva em forma simples;
• não pode ser resolvido analiticamente;
• equações diferenciais parciais não lineares podem ser
resolvidas analiticamente só em casos particulares.
08/09/134
∫ dxex2
22
tyy +=′
Cálculo Numérico
Aplicações

5. Na engenharia, são várias as motivações para seu uso:
• Ganho de tempo: solucionar em curto espaço de
tempo problemas que tomariam muito tempo para
serem solucionados
• Economia de recursos: não ocupar engenheiros e
outros recursos na construção de soluções
• Simplificar problemas complexos: com a
modelagem adequada, problemas mais simples, ou
de simples soluções podem corresponder a
problemas mais complexos, mantida a qualidade da
resposta.
08/09/135
Cálculo Numérico
Aplicações

6. Os métodos numéricos buscam soluções aproximadas. Com
determinadas condições de contorno, em problemas
simples ou em situações específicas, pode-se obter
respostas exatas. Isto é um fato desejado, mas nunca
será o objetivo do cálculo numérico.
Somente são solucionáveis numericamente problemas que
podem ser modelados matematicamente, portanto deve-
se conhecer a natureza do problema antes de encontrar
as soluções.
08/09/136
Cálculo Numérico
Limitações

7. Em problemas baseados em dados reais, dados medidos ou
obtidos por instrumentos sujeitos à imprecisão humana,
estes dados jamais serão exatos. Uma medida física
deve ser sempre tomada não como um número único e
extremamente preciso, mas como um intervalo, um
conjunto de valores dentro de um certo limite de
tolerância.
Assim o cálculo numérico não falha em possuir erros, mas
reflete com mais fidelidade a realidade.
08/09/137
Cálculo Numérico
Limitações

8. 08/09/138
Cálculo Numérico
Fluxo de uso
Entender o ProblemaEntender o Problema
Modelar o ProblemaModelar o Problema
Implementar o modeloImplementar o modelo
Encontrar a SoluçãoEncontrar a Solução