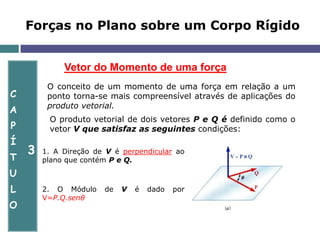
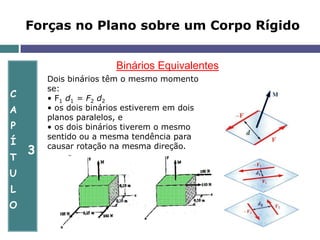
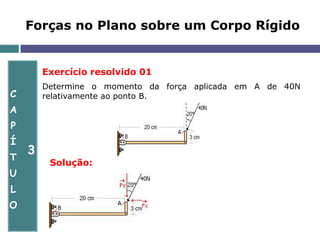
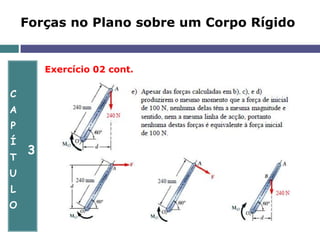
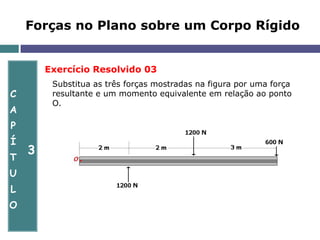
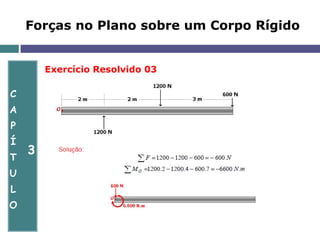
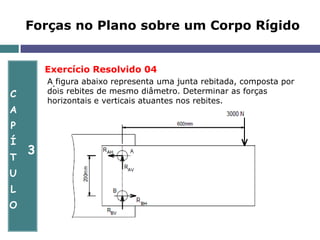
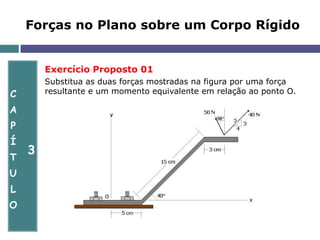
O documento aborda a mecânica de corpos rígidos, focando na atuação de forças, momentos e torques que causam rotação. Ele explora conceitos como produto vetorial, teorema de Varignon e a equivalência de forças, além de apresentar exercícios resolvidos para aplicar esses conceitos. Também discute a determinação de reações nos apoios e o equilíbrio de estruturas em duas dimensões.

1. MECÂNICA GERAL
PARA ENGENHEIROS
Profª: Acilayne Freitas de Aquino
Capítulo 3

2. Forças no Plano sobre um Corpo Rígido
C
A
P
Í
T
U
L
O
3
Profª: Acilayne Freitas
CORPO RÍGIDO
O corpo rígido é dotado de dimensões que poderão ser
importantes para a determinação das forças externas
envolvidas nos sistemas de força. Em uma partícula os
efeitos da atuação de forças eram apenas a translação ou
repouso. Já em corpos rígidos, a atuação de forças, além de
poder promover translação ou repouso, poderá ocasionar
rotação (momento de uma força).
Em mecânica elementar assumimos que a maior parte
dos corpos são rígidos, isto é, as deformações são
pequenas e não afetam as condições de equilíbrio ou os
movimentos dos corpos.

3. C
A
P
Í
T
U
L
O
3
Momento de uma Força (Torque)
Forças no Plano sobre um Corpo Rígido
Também conhecido como torque, o momento de uma força
aplicada em A em relação a um ponto B representa a tendência
da força aplicada em A em causar um giro no corpo em torno do
ponto B.
A intensidade do momento é definida como produto da
componente da força que efetivamente promove o giro (Fe) e a
distância (d) (braço de alavanca) do ponto de aplicação da
força e o ponto de giro (polo). Assim:
MB = Fe.d = F.senθ .d
O vetor d é a distância
perpendicular de B à linha de
ação de F.

4. C
A
P
Í
T
U
L
O
3
Vetor do Momento de uma força
Forças no Plano sobre um Corpo Rígido
O conceito de um momento de uma força em relação a um
ponto torna-se mais compreensível através de aplicações do
produto vetorial.
O produto vetorial de dois vetores P e Q é definido como o
vetor V que satisfaz as seguintes condições:
1. A Direção de V é perpendicular ao
plano que contém P e Q.
2. O Módulo de V é dado por
V=P.Q.senθ

5. C
A
P
Í
T
U
L
O
3
Vetor do Momento de uma força
Forças no Plano sobre um Corpo Rígido
3. O Sentido Direção de V é dado pela regra da mão
direita
• Qualquer força F’ que tenha a mesma magnitude e
direção que F, é equivalente se também tem a
mesma linha de ação e consequentemente produz o
mesmo momento.
Forças Equivalentes

6. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Teorema de Varignon
O momento em relação a um dado ponto O resultante de
diversas forças concorrentes é igual à soma dos momentos
das diversas forças em relação ao mesmo ponto O.

7. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Momento de um Binário
Duas forças F e –F que tenham o mesmo módulo, linhas de
ação paralelas e sentidos opostos formam um binário.
A soma das componentes das duas forças em qualquer
direção é zero. Entretanto, a soma dos momentos das
duas forças em relação a um dado ponto não é zero.
Pois as forças tendem a girar o corpo.
O momento produzido pelo binário será dado por:
M=Fxb

8. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Binários Equivalentes
Dois binários têm o mesmo momento
se:
• F1 d1 = F2 d2
• os dois binários estiverem em dois
planos paralelos, e
• os dois binários tiverem o mesmo
sentido ou a mesma tendência para
causar rotação na mesma direção.

9. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício resolvido 01
Determine o momento da força aplicada em A de 40N
relativamente ao ponto B.
Solução:

10. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Solução:

11. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício resolvido 02
Uma força vertical de 100 N é aplicada na
extremidade de uma alavanca que está fixa em O
240 mm
100 N
Determine:
a) O momento da força de 100 N em relação ao
ponto O;
b) A intensidade da força horizontal aplicada em
A que produz o mesmo momento em relação ao
ponto O;
c) A menor força em A que produz o mesmo
momento em relação ao ponto O;
d) A que distância do eixo deverá estar uma
força vertical de 240 N de modo a produzir o
mesmo momento em relação ao ponto O,
e) Se alguma das forças obtidas nas alíneas b),
c) e d) é equivalente à força original.

12. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício 02 cont.

13. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício 02 cont.

14. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício 02 cont.

15. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício 02 cont.

16. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício 02 cont.

17. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício Resolvido 03
Substitua as três forças mostradas na figura por uma força
resultante e um momento equivalente em relação ao ponto
O.

18. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício Resolvido 03

19. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício Resolvido 04
.A figura abaixo representa uma junta rebitada, composta por
dois rebites de mesmo diâmetro. Determinar as forças
horizontais e verticais atuantes nos rebites.

20. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício Resolvido 04
Como os rebites são iguais, as cargas e as reações verticais em
cada rebite também são iguais: RAV= RBV= 3000÷2= 1500 N.
O rebite A está sendo “puxado” para a direita, portanto, possuirá
uma reação horizontal para a esquerda;
O rebite B está sendo “empurrado” para a esquerda,
portanto, possuirá uma reação horizontal para a direita.
Determinação dos esforços horizontais:
Σ A = 0 M
RBH×200=3000×600 = 9000 N
RAH= RBH=9000 N

21. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício Proposto 01
Substitua as duas forças mostradas na figura por uma força
resultante e um momento equivalente em relação ao ponto O.

22. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Equilíbrio dos Corpos Rígidos

23. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Equilíbrio em duas dimensões
Equilíbrio dos Corpos Rígidos

24. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Apoios

25. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Apoios

26. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Tipos de Estrutura
1- Estrutura hipostática

27. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Tipos de Estrutura
2- Estrutura Isostática

28. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Tipos de Estrutura
3- Estrutura hiperestática

29. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício Resolvido 01
Determine as reações nos apoios A e B da viga ilustrada
abaixo.

30. C
A
P
Í
T
U
L
O
3
Forças no Plano sobre um Corpo Rígido
Exercício Resolvido 01
Diagrama de corpo livre da viga