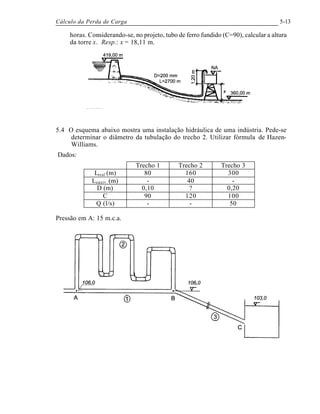
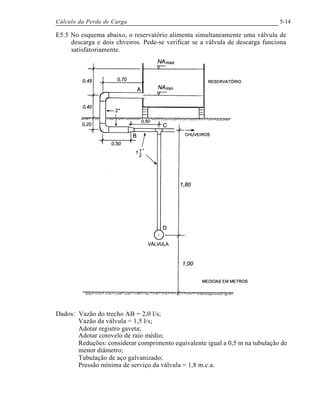
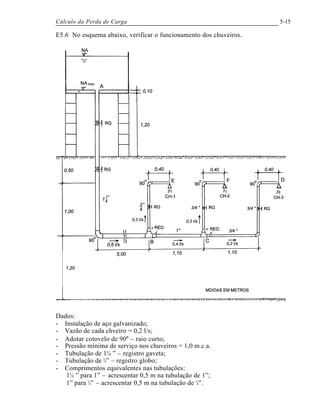
O documento descreve os métodos para calcular a perda de carga em tubulações circulares, apresentando: 1) A fórmula universal para perda de carga em função de variáveis como comprimento, diâmetro, vazão e fator de atrito; 2) Os regimes de escoamento (laminar, transição, turbulento liso, misto e rugoso) e como calcular o fator de atrito para cada um; 3) Algoritmos para três problemas típicos de cálculo de perda de carga, resolvendo para vazão, diferença

1. Cálculo da Perda de Carga 5-1
5 CÁLCULO DA PERDA DE CARGA
5.1 Perda de Carga Distribuída
5.1.1 Fórmula Universal
Aplicando-se a análise dimensional ao problema do movimento de fluidos em
tubulações de seção circular, encontra-se a seguinte expressão para a perda de carga,
conhecida como fórmula universal:
g
V
D
L
fH
2
2
=∆ (5.1)
onde: L é o comprimento do encanamento em m;
V é a velocidade média do fluido em m/s;
D é o diâmetro da canalização em m;
f é o fator de atrito;
∆H é a perda de carga em m.
A Equação 5.1 pode ser escrita também em termos de vazão Q:
gD
QLf
H
⋅⋅
⋅⋅⋅
=∆ 52
2
8
π
(5.2)
5.1.1.1 O fator de atrito f
O fator de atrito f, sem dimensões, é função do número de Reynolds e da rugosidade
relativa. A espessura ou altura k das asperezas (rugosidade) dos tubos pode ser avaliada
determinando-se valores para k/D.
Conforme já visto no capítulo 4, o número de Reynolds qualifica o regime de
escoamento em laminar (Re < 2.000), turbulento (Re > 4.000) ou crítico. O regime
completamente turbulento (rugoso) é atingido com valores ainda mais elevados do
número de Reynolds, existindo, portanto, uma segunda zona intermediária, conhecida
como zona de transição (Figura 5.1).
Os valores do fator de atrito f são obtidos
em função do número de Reynolds e da
rugosidade relativa, tendo-se em vista o regime
de escoamento.
Regime laminar → f = f (Re)
Regime turbulento liso → f = f (Re)
Regime turbulento de transição entre o liso e o
rugoso → f = f (Re,
D
k
)
Regime turbulento rugoso → f = f (
D
k
) Figura 5.1

2. Cálculo da Perda de Carga 5-2
5.1.1.2 Determinação do fator de atrito f
Em vez de consultar o Diagrama de Moody-Rouse, como se fez tradicionalmente
em Hidráulica, foi introduzido, neste curso, o método de cálculo proposto pelo Prof.
Podalyro Amaral de Souza da EPUSP, o qual consiste em criar alguns adimensionais
para a obtenção do fator de atrito. A definição desses adimensionaisdependedotipode
problemas existentes no projeto de condutos forçados.
A seguir são apresentados os problemas típicos do projeto de encanamentos
encontrados na prática e a sua solução, na forma de algoritmos:
a) Problema tipo 1 – Cálculo de Q
Dados: ∆H, L, D, k, ν, g
Incógnita: Q ?
1. Calcular
L
HDgD
fR
∆⋅⋅
=
2
ν
2. Se fR ≤ 400 → regime laminar →
2
64








=
fR
f → ir para o passo 8;
3. Se 400 < fR < 800 → região crítica → não se calcula o f → Fim.
4. Se fR > 800 → regime turbulento → calcular
kD
fR
/
5. Se
kD
fR
/
≤ 14 → regime turbulento liso →
2
51,2
log2
−
















−=
fR
f → ir para o
passo 8;
6. Se 14 <
kD
fR
/
< 200 → regime turbulento misto →
2
51,2
71,3
log2
−
















+−=
fRD
k
f
→ ir para o passo 8;
7. Se
kD
fR
/
≥ 200 → regime turbulento rugoso →
2
71,3
log2
−












−=
D
k
f
8. Calcular
2
1
52
8 





⋅⋅
∆⋅⋅⋅
=
Lf
HgD
Q
π
9. Fim
b) Problema tipo 2 – Cálculo de ∆∆H
Dados: Q, D, L, ν, k, g
Incógnita: ∆H ?

3. Cálculo da Perda de Carga 5-3
1. Calcular
νπ ⋅⋅
=
D
Q
R
4
2. Se R ≤ 2.500 → regime laminar →
R
f
64
= → ir para o passo 8;
3. Se 2.500 < R < 4.000 → região crítica → não se calcula o f → Fim.
4. Se R > 4.000 → regime turbulento → calcular
kD
R
/
9,0
5. Se
kD
R
/
9,0
≤ 31 → regime turbulento liso →
2
9,0
62,5
log2
−












−=
R
f → ir para
o passo 8;
6. Se 31 <
kD
R
/
9,0
< 448 → regime turbulento misto →
2
9,0
62,5
71,3
log2
−












+−=
RD
k
f →
ir para o passo 8;
7. Se
kD
R
/
9,0
≥ 448 → regime turbulento rugoso →
2
71,3
log2
−












−=
D
k
f
8. Calcular
gD
QLf
H
⋅⋅
⋅⋅⋅
=∆ 52
2
8
π
9. Fim
c) Problema tipo 3 – Cálculo de D
Dados: Q, ∆H , L, ν, k, g
Incógnita: D ?
1. Calcular
νπ ⋅⋅
⋅
=
k
Q
M
4
e
2,0
3
3
1281






⋅
∆⋅⋅
=
L
HQg
N
πν
2. Se N ≤ 1.200 → regime laminar → 25,1
181
N
f = → ir para o passo 8;
3. Se 1.200 < N < 2.100 → região crítica → não se calcula o f → Fim.
4. Se N > 2.100 → regime turbulento → calcular
M
N 2
5. Se
M
N 2
≤ 17 → regime turbulento liso →
2
937,0
15,4
log2
−












−=
N
f → ir para o
passo 8;
6. Se 17 <
M
N 2
< 236 → regime turbulento misto →

4. Cálculo da Perda de Carga 5-4
2
937,0
042,1
15,438,0
log2
−












+−=
NM
N
f → ir para o passo 8;
7. Se
M
N 2
≥ 236 → regime turbulento rugoso →
2
042,1
38,0
log2
−












−=
M
N
f
8. Calcular
5
1
2
2
8






∆⋅⋅
⋅⋅⋅
=
Hg
LQf
D
π
9. Fim
EXERCÍCIOS-EXEMPLOS
5.1 Um reservatório está sendo alimentado diretamente de uma represa, conforme mostra
a figura abaixo. Determine o nível d´água NA2 do reservatório, sabendo-se que o
nível d´água da represa está na cota 50 m.
Dados: Q = 200 l/s
k = 5 mm
D = 400 mm
L = 750 m
ν = 1,01 x 10-6
m2
/s
Solução: Para determinar a cota NA2, é necessário calcular inicialmente a perda de carga
∆H. Portanto, trata-se do problema tipo 2.
- Cálculo da velocidade:
m/s59,1
)40,0(
2,04
2
=
×
×
==
πA
Q
V
- Cálculo do Nº de Reynolds:
703.629
1001,1
4,059,1
6
=
×
×
=
⋅
= −
ν
DV
R > 4.000 ⇒ regime turbulento
- Cálculo do adimensional
kD
R
/
9,0
:
2071
)5/400(
703.629
/
9,09,0
==
kD
R
> 448 ⇒ regime turbulento rugoso
- Cálculo de f:
0409,0
40071,3
5
log2
71,3
log2
22
=











×
−=











⋅
−=
−−
D
k
f
- Cálculo da perda de carga:

5. Cálculo da Perda de Carga 5-5
m90,9
81,9)40,0(
)20,0(7500409,088
52
2
52
2
=
××
×××
=
⋅⋅
⋅⋅⋅
=∆
ππ gD
QLf
H
NA2 = 50,00 – 9,90 = 40,10 m
5.2 Determine a vazão transportada pela adutora que liga uma represa e um
reservatório, conforme mostra a figura.
Dados: L = 360 m
D = 0,15 m
k = 0,00026 m
ν = 10-6
m2
/s
Solução: A incógnita é a vazão ∴ é problema do tipo 1.
- Cálculo da adimensional fR :
360.41
360
15,03,981,92
10
15,02
6
=
×××
×=
⋅∆⋅
⋅= −
L
DHgD
fR
ν
> 800 ⇒ reg. turbulento
- Cálculo do adimensional
kD
fR
/
:
7,71
)00026,0/15,0(
360.41
/
==
kD
fR
⇒ 14 < 71,7 < 200 ⇒ reg. turbulento misto
- Cálculo de f:
0233,0
360.41
51,2
15,071,3
00026,0
log2
51,2
71,3
log2
22
=











+
×
−=
















+
⋅
−=
−−
fRD
k
f
- Cálculo da vazão:
Lf
HgD
gD
QLf
H
⋅⋅
∆⋅⋅⋅
=⇒
⋅⋅
⋅⋅⋅
=∆
8
Q
8 52
52
2
π
π
3600233,08
3,981,9)15,0(
Q
52
××
×××
=
π
= 0,0319 m3
/s ou 31,9 l/s
EXERCÍCIOS PROPOSTOS
E5.1 A tubulação que liga uma represa e um reservatório tem 1.300 m de comprimento e
600 mm de diâmetro e é executada em concreto com acabamento comum (k = 0,4
mm). Determinar a cota do nível d´água (NA1) na represa sabendo-se que a vazão
transportada é de 250 l/s e que o nível d´água no reservatório inferior (NA2)estána
cota 10,00 m. Desprezar as perdas localizadas e adotar νágua = 10-6
m2
/s.

6. Cálculo da Perda de Carga 5-6
E5.2 Para a instalação da figura, determinar o valor de a,sabendo-se que a vazão é 10 l/s
e que o conduto é de ferro fundido novo (k = 0,25 mm).
E5.3 O conduto da figura tem rugosidade k =
0,25 mm e o diâmetro D = 150 mm.
Determinar o comprimento L do
conduto, sabendo-se que está escoando
uma vazão de 50 l/s. Desprezar as
perdas localizadas e adotar νágua = 10-6
m2
/s.
E5.4 Determine a vazão que escoa através da tubulação que interliga dois reservatórios,
conforme mostra a figura abaixo
.Dados: L = 150 m
k = 0,0035 mm
D = 200 mm
νágua = 10-6
m2
/s
5.1.2 Fórmulas Práticas
Embora a fórmula universal seja recomendada para o cálculo de perdas distribuídas,
algumas fórmulas práticas são aceitas largamente até hoje, tendo em vista as
confirmações experimentais. Dentre elas, são apresentadas as duas mais empregadas
atualmente:

7. Cálculo da Perda de Carga 5-7
a) Fórmula de Hazen-Williams (1903)
É uma fórmula que resultou de um estudo estatístico com grande número de dados
experimentais e é expressa pela seguinte equação:
87,485,1
85,1
643,10
DC
Q
J = . (5.3)
ou, em termos de vazão:
54,063,2
279,0 JDCQ ⋅⋅⋅= (5.4)
onde:
Q é a vazão em m3/s;
D é o diâmetro da tubulação em m;
J é a perda de carga unitária em m/m;
C é o coeficiente que depende da natureza (material e estado) das paredes dos
tubos. A Tabela 5.1 mostra alguns valores do coeficiente C.
A perda de carga total é dada por:
∆H = J x L (5.5)
onde ∆H é a perda de carga em m e L é o comprimento da tubulação em m.
Esta fórmula pode ser satisfatoriamente aplicada para qualquer tipo de conduto e de
material. Os seus limites de aplicação são os mais largos: diâmetro de 50 a 3.500 mm.
Tabela 5.1 – Valor do coeficiente C.
Tubos C
Aço galvanizado (novos e em uso)
Cimento-amianto
Concreto, bom acabamento
Concreto, acabamento comum
Ferro fundido, novos
Ferro fundido, em uso
125
140
130
120
130
90
b) Fórmula de Fair-Whipple-Hsiao (1930)
São fórmulas recentes, estabelecidas para os encanamentos de pequeno diâmetro
(até 50 mm). Para todas as equações abaixo, Q é a vazão m3
/s, D é o diâmetro em m e J é
a perda de carga unitária em m/m.
• Canos de aço galvanizado conduzindo água fria.
88,4
88,1
002021,0
D
Q
J = (5.6)
ou, 596,2532,0
113,27 DJQ ⋅⋅= (5.7)
• Canos de cobre ou latão conduzindo água fria.

8. Cálculo da Perda de Carga 5-8
75,4
75,1
000874,0
D
Q
J = (5.8)
ou, Q = 55,934.D 2,71
.J 0,57
(5.9)
• Canos de cobre ou latão conduzindo água quente.
75,4
75,1
000704,0
D
Q
J = (5.10)
Q = 63,281.D 2,71
.J 0,57
(5.11)
Da mesma forma que a fórmula de Hazen-Williams, a perda de carga total é dada
por:
∆H = J x L (5.5)
onde ∆H é a perda de carga em m e L é o comprimento da tubulação em m.
5.2 Perda de Carga Localizada
Conforme visto no capítulo 4, a perda de carga localizada é devida à
descontinuidade da tubulação, chamada singularidade, que pode ser peças especiais de
mudança de direção (curva, cotovelo) ou alteração de velocidade (redução, alargamento,
registro, etc.).
De um modo geral, todas as perdas localizadas podem ser expressas sob a forma
g
V
K
2
2
=λ (5.12)
onde λ é a perda de carga localizada;
V é a velocidade de escoamento;
K é o coeficiente de perda de carga localizada, obtido experimentalmente para cada
caso. A Tabela 5.2 apresenta os valores aproximados de K para as peças e perdas
mais comuns na prática.
Tabela 5.2 – Valores aproximados de K.
Peça K
Bocais
Comporta aberta
Cotovelo de 90°
Cotovelo de 45°
Curva de 90°
Curva de 45°
Entrada de borda
Saída de canalização
Tê, passagem direta
Válvula de gaveta aberta
2,75
1,00
0,90
0,40
0,40
0,20
1,00
1,00
0,60
0,20

9. Cálculo da Perda de Carga 5-9
Método dos comprimentos equivalentes (ou virtuais)
O método considera que uma canalização que compreende diversas singularidades,
sob o ponto de vista de perda de carga, equivale a um encanamento retilíneo de
comprimento maior.
Para simples efeito de cálculo, o método consiste em adicionar à extensão da
canalização, comprimentos tais que correspondam à mesma perda que causariam as peças
especiais existentes na canalização. A cada singularidade corresponde um certo
comprimento fictício. Os valores de comprimento equivalente correspondentes a diversas
peças podem ser encontrados em qualquer manual de Hidráulica.
A tabela da página seguinte apresenta os comprimentos equivalentes a perdas
localizadas de algumas singularidades.
EXERCÍCIOS-EXEMPLOS
5.3 Calcular o diâmetro de uma tubulação de aço usada (C=90), com 3.000 m de
comprimento, que veicula uma vazão de 250 l/s com uma perda de carga de 51 m.
Solução:
∆H = 51 m; Q = 0,25 m3
/s
m/m017,0
000.3
51
==
∆
=
L
H
J
54,063,2
279,0 JDCQ ⋅⋅⋅=
54,0
63,2
279,0 JC
Q
D
⋅⋅
=
=





××
=





⋅⋅
=
63,2
1
54,0
63,2
1
54,0
017,090279,0
25,0
279,0 JC
Q
D 0,400 m
5.4 Uma canalização de ferro dúctil com 1800 m de comprimento e 300 mm de diâmetro
está descarregando, em um reservatório, 60 l/s. calcular a diferença de nível entre a
represa e o reservatório, considerando todas as perdas de carga. Verificar quanto as
perdas locais representam da perda por atrito ao longo do encanamento (em %). Há
na linha apenas 2 curvas de 90°, 2 de 45° e 2 registros de gaveta (abertos).
Solução:
Q = V.A => m/s85,0
)30,0(
06,044
22
=
×
×
=
⋅
⋅
==
ππ D
Q
A
Q
V
Curva de 90° à K = 0,40

10. Cálculo da Perda de Carga 5-10

11. Cálculo da Perda de Carga 5-11
Curva de 45° à K = 0,20
Registro de gaveta (aberto) à K = 0,20
Entrada da canalização à K = 1,00
Saída da canalização à K = 1,00
Ktot = 2 x 0,40 + 2 x 0,20 + 2 x 0,20 +2 x 1,00= 3,6
Perda de carga localizada total:
m133,0
81,92
)85,0(
6,3
2
22
=
×
×=⋅=
g
V
Kλ
Perda de carga distribuída:
Fórmula de Hazen-Williams:
=
×
×== 87,485,1
85,1
87,485,1
85,1
)30,0(100
)06,0(
643,10643,10
DC
Q
J 0,0041 m/m
∆H = J x L = 0,0041 x 1800 = 7,38 m
Perda de carga total:
Porcentagem da perda localizada em relação à perda distribuída:
018,0
38,7
133,0
==ε ou 1,8%
5.5 Determinar a carga disponível no chuveiro de
uma instalação predial, abastecido por um
ramal de ¾’’. Utilizar o método de
comprimento virtual e a fórmula de Fair-
Whiple-Hsiao para calcular a perda de carga.
Solução:
Aplicando o método dos comprimentos
equivalentes às perdas singulares:
No ramal (tubulação de ¾’’):
Singularidade Comprimento virtual
(em m de canalização)
Tê, saída do lado 1,4
Cotovelo de 90°, raio curto 0,7
Registro de gaveta aberto 0,1
Comprimento equivalente total no ramal: LVR = 1,4 + 5 x 0,7 + 2 x 0,1 = 5,1 m
Comprimento real do ramal: LRR = 0,35 + 1,10 + 1,65 + 1,0 + 0,50 + 0,20 = 5,3 m
Comprimento total do ramal: LTR = 5,1 + 5,3 = 10,4 m

12. Cálculo da Perda de Carga 5-12
Cálculo da perda de carga:
Fórmula de Fair-Whiple-Hsiao:
m/m0557,0
)01905,0(
)0002,0(
002021,0002021,0 88,4
88,1
88,4
88,1
=×==
D
Q
J
∆HR = J x L = 0,0557 x 10,4 = 0,58 m
Na tubulação principal (tubulação de 1½’’):
Comprimento virtual da tubulação principal: LVP = 0,5 m (entrada normal)
Comprimento real da tubulação principal: LRP = 0,9 m
Comprimento total da tubulação principal: LTP = 0,5 + 0,9 = 1,4 m
m/m0390,0
)0381,0(
)001,0(
002021,0002021,0 88,4
88,1
88,4
88,1
=×==
D
Q
J
∆HP = J x L = 0,0390 x 1,4 = 0,05 m
Carga geométrica: 1,7 m (da figura)
Carga disponível no chuveiro: Hdisp = 1,70 – 0,58 – 0,05 = 1,07 m (caixa d´água cheia)
EXERCÍCIOS PROPOSTOS
E5.1 Calcular a vazão que escoa por um conduto de ferro fundido usado (C=90), de 200
mm de diâmetro, desde um reservatório na cota 200 m até outro reservatório na cota
zero. O comprimento do conduto é de 10.000 m. Resp.: Q = 0,044 m3
/s.
E5.2 Deseja-se transportar 1.130 l/s de água com a velocidade de 1m/s em uma tubulação
de 500 m de comprimento, com C=100. Calcular a perda de carga. Resp.: ∆H = 5,5
m.
E5.3 O abastecimento de água de uma indústria será feita a parir de um reservatório
elevado, que recebe água de uma represa. O consumo máximo diário da indústria é
de 800 m3
e a adutora deverá ter capacidade para transportar esse volume em 6

13. Cálculo da Perda de Carga 5-13
horas. Considerando-se, no projeto, tubo de ferro fundido (C=90), calcular a altura
da torre x. Resp.: x = 18,11 m.
5.4 O esquema abaixo mostra uma instalação hidráulica de uma indústria. Pede-se
determinar o diâmetro da tubulação do trecho 2. Utilizar fórmula de Hazen-
Williams.
Dados:
Trecho 1 Trecho 2 Trecho 3
Lreal (m) 80 160 300
Lequiv. (m) - 40 -
D (m) 0,10 ? 0,20
C 90 120 100
Q (l/s) - - 50
Pressão em A: 15 m.c.a.

14. Cálculo da Perda de Carga 5-14
E5.5 No esquema abaixo, o reservatório alimenta simultaneamente uma válvula de
descarga e dois chveiros. Pede-se verificar se a válvula de descarga funciona
satisfatoriamente.
Dados: Vazão do trecho AB = 2,0 l/s;
Vazão da válvula = 1,5 l/s;
Adotar registro gaveta;
Adotar cotovelo de raio médio;
Reduções: considerar comprimento equivalente igual a 0,5 m na tubulação de
menor diâmetro;
Tubulação de aço galvanizado;
Pressão mínima de serviço da válvula = 1,8 m.c.a.

15. Cálculo da Perda de Carga 5-15
E5.6 No esquema abaixo, verificar o funcionamento dos chuveiros.
Dados:
- Instalação de aço galvanizado;
- Vazão de cada chveiro = 0,2 l/s;
- Adotar cotovelo de 90° – raio curto;
- Pressão mínima de serviço nos chuveiros = 1,0 m.c.a.
- Tubulação de 1¼ ” – registro gaveta;
- Tubulação de ¾” – registro globo;
- Comprimentos equivalentes nas tubulações:
1¼ ” para 1” – acrescentar 0,5 m na tubulação de 1”;
1” para ¾” – acrescentar 0,5 m na tubulação de ¾”.