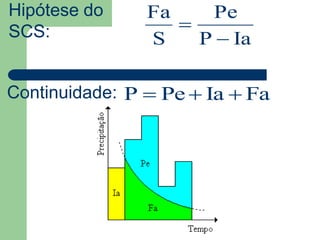
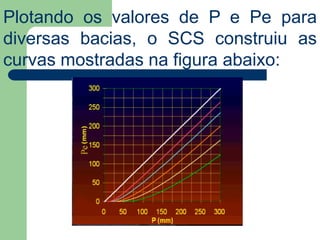
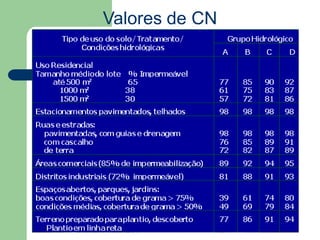
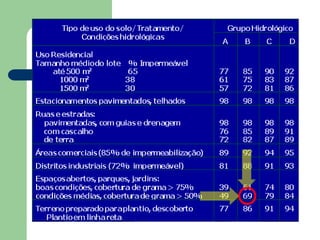
O documento descreve o plano de ensino de uma disciplina de Hidráulica e Hidrologia Aplicada sobre Canais. O plano inclui carga horária, desenvolvimento da disciplina, ementa, objetivos gerais e específicos, conteúdo programático, avaliação e bibliografia.