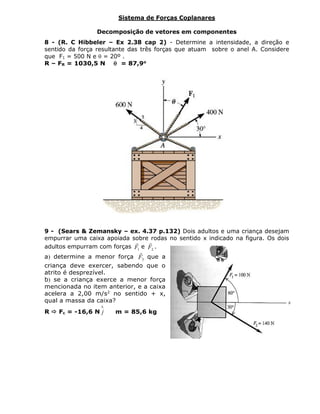
1) O documento apresenta uma lista de exercícios sobre leis dos cossenos e senos e decomposição de vetores em componentes. 2) Inclui exercícios sobre determinação de forças resultantes, ângulos e intensidades utilizando as leis dos cossenos e senos. 3) Também aborda exercícios sobre equilíbrio de sistemas de forças coplanares e determinação de vetores de força e posição.

1. Lista de Exercícios - Aula 01
Lei dos Cossenos e Senos
5 – (R. C Hibbeler – Mecânica - Estática –exemplo 2.1 p.16). O parafuso tipo
gancho da figura está sujeito a duas forças F1 e F2. Determine a intensidade da
força resultante utilizando a lei dos cossenos.
R  FR = 25,24 kN
6 – (R. C Hibbeler – Mecânica – Estática) Determine a intensidade da força
resultante .
R  FR = 212,5 N
7 - Determine o ângulo  necessário para acoplar o elemento A à chapa, de modo
que a força resultante de FA e FB seja orientada horizontalmente para a direita.
Além disso, informe qual é a intensidade da força resultante.
FA = 10,4 kN  = 54,93o

2. Sistema de Forças Coplanares
Decomposição de vetores em componentes
8 - (R. C Hibbeler – Ex 2.38 cap 2) - Determine a intensidade, a direção e
sentido da força resultante das três forças que atuam sobre o anel A. Considere
que F1 = 500 N e  = 20º .
R – FR = 1030,5 N  = 87,9o
9 - (Sears & Zemansky – ex. 4.37 p.132) Dois adultos e uma criança desejam
empurrar uma caixa apoiada sobre rodas no sentido x indicado na figura. Os dois
adultos empurram com forças 1F

e 2F

.
a determine a menor força 3F

que a
criança deve exercer, sabendo que o
atrito é desprezível.
b se a criança exerce a menor força
mencionada no item anterior, e a caixa
acelera a 2,00 m/s2
no sentido + x,
qual a massa da caixa?
R  Fc = -16,6 N

j m = 85,6 kg

3. 10 - Denomina-se treliça plana, o conjunto de elementos de construção
(barras redondas, chatas, cantoneiras), interligados entre si, sob forma
geométrica triangular, através de pinos, soldas, rebites, parafusos, que visam
formar uma estrutura rígida, com a finalidade de resistir a esforços normais
apenas. A denominação treliça plana deve-se ao fato de todos os elementos do
conjunto pertencer a um único plano. A sua utilização na prática pode ser
observada em pontes, viadutos, coberturas, guindastes, torres, etc.
Todas as cargas são aplicadas aos nós, normalmente o peso próprio é
desprezado pois a carga suportada é bem maior que o peso do elemento. Para
que o sistema esteja em equilíbrio a resultante das forças em cada nó deve ser
nula. Entretanto um engenheiro ao projetar uma estrutura errou no calculo do
valor do ângulo , gerando uma força resultante no nó, comprometendo o
equilíbrio da estrutura. Encontre o valor do vetor força resultante do sistema,
sua intensidade e sua direção.
R – F =

rF =
11 - Os cabos de sustentação AB e AC estão presos no topo da torre de
transmissão. A força trativa no cabo AC vale 8 kN.
a) Determine a força trativa T necessária no cabo AB, tal que o efeito
resultante das duas forças trativas nos cabos seja uma força direcionada
para baixo no ponto A. (lei dos senos)
b) Determine o vetor força em cada cabo e a intensidade do vetor resultante.
FA = 8.000 N
FB = 14.000 N
FD = 5.000 N
FC = 12.000 N
35º
50º

4. 12 - Um cabo esticado entre os suportes fixo A e B
está sob uma tração de 900 N. Expresse esta força
que atua no ponto A na forma de vetor.
13 - R. C. Hibbeler 2.82 12ª Ed – Determine o vetor posição r direcionado do
ponto A ao ponto B e o comprimento da corda AB. Considere z = 4 m.
FAB = (- 3i + 6j + 2k ) m d = 7 m
14 - R. C. Hibbeler 2.106 A torre é mantida reta pelos três cabos. Se a força em
cada cabo que atua sobre a torre for aquela mostrada na figura, determine a
intensidade e os ângulos diretores coordenados α, β, γ da força resultante.
Considere que x = 20 m, y = 15m.
FR = 1,5 kN  = 77,6 o
 = 90,6 o
 = 168 o

5. Leis de Newton
1 - Na superfície da Terra a aceleração da gravidade vale 9,8m/s2
e, na superfície da Lua
1,6m/s2
e no Sol 274m/s2
. Para um corpo de massa igual a 70kg, calcule:
a) o peso na superfície da Terra;
b) o peso na superfície da Lua;
c) o peso na superfície do Sol.
2 - Um corpo de massa igual a 5kg move-se com velocidade de 10m/s. Qual a
intensidade da força que se deve aplicar nele de modo que após percorrer 200m
sua velocidade seja 30m/s?
3 - Um automóvel em trajetória reta tem massa 1.512kg e uma velocidade inicial
de 72km/h. Quando os freios são acionados, para produzir uma desaceleração
constante, o carro para em 12s. A força aplicada ao carro é igual, em newtons, a:
4 - (Cap. 4 Exemplo 4-2 – pág 96 Tipler 5a ed – pág 98 6a ed) Imagine que
você está flutuando no espaço, longe de sua nave espacial. Felizmente, você
dispõe de uma unidade de propulsão capaz de propiciar uma força constante
F

durante 3 s. Após 3 s de acionamento da unidade, o seu deslocamento foi
de 2,25 m. Considerando que sua massa seja de 68 kg, determine F

. R – 34
N
5 - ( Sears & Zemansky Física I ex 4.38 pág 132) R  v = 0,17 m/s
Os motores de um navio-tanque enguiçaram e o vento está levando o navio
diretamente para um recife, a uma velocidade escalar constante de 1,5 m/s.
Quando o navio está a 500 m do recife, o vento cessa e os motores voltam a
funcionar. O leme está emperrado, e a única alternativa é tentar acelerar
diretamente para trás, para se afastar do recife. A massa do navio e da carga é de
3,6 . 107
kg, e os motores produzem uma força resultante horizontal de 8,0 . 104
N
sobre o navio. Ele atingirá o recife? Se sim, o petróleo estará seguro? O casco
resiste ao impacto de uma velocidade escalar de até 0,2 m/s. Ignore a força
retardadora da água sobre o casco do navio-tanque.
6 - (Cap. 4 Ex 37 pág 120 5a ed -Ex 41 pág 117 6a ed) Um objeto de 4,0 kg é
submetido a duas forças

1F = 2 N

i - 3 N

j e

2F = 4 N

i - 11 N

j . O objeto está em
repouso na origem no tempo t =0 . a) Qual a aceleração do objeto? b) Qual é sua
velocidade no tempo t= 3,0s ? c) Onde está o objeto no tempo t = 3,0 s?
a)

a = 1,5 m/s2

i - 3,5 m/s2

j b)

v = 4,5 m/s

i - 10,5 m/s

j
c)

r = 6,75 m

i - 15,8 m

j