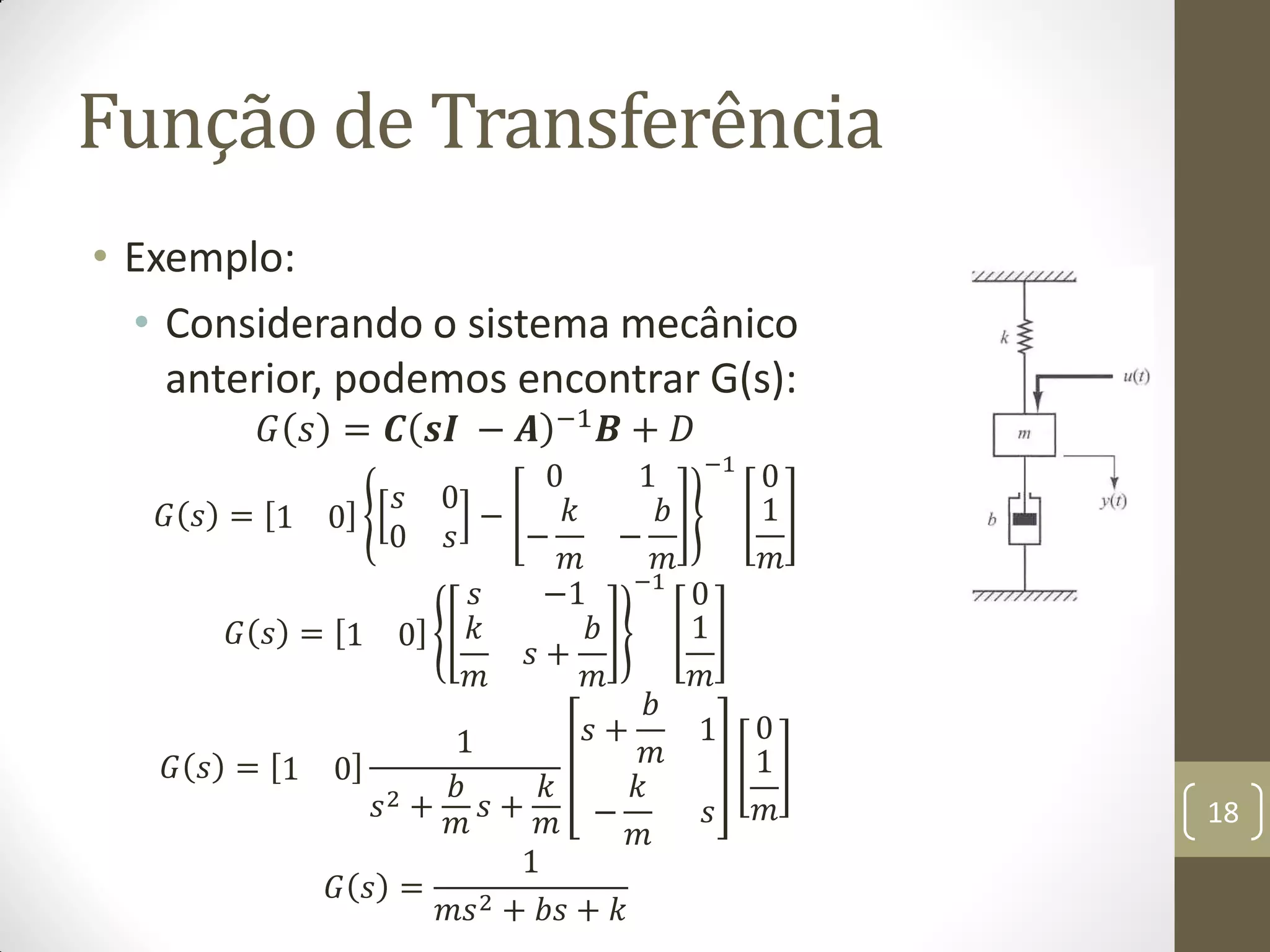
O documento discute os conceitos fundamentais da teoria de controle moderno no espaço de estados, incluindo: 1) o conceito de estado e variáveis de estado que determinam completamente o comportamento de um sistema, 2) a representação do sistema através de equações no espaço de estados e 3) a obtenção da função de transferência a partir da representação no espaço de estados.

1. Estudos de Controle
– Espaço de Estados
1

2. Teorias Controle
• Teoria de Controle Moderno
• Entradas e saídas múltiplas, podendo ser
variantes no tempo.
• Abordagem no domínio do tempo.
• Possibilidade de lidar com sistemas não-
lineares.
• Base no conceito de estado.
2

3. Definições
• Estado:
• É o menor conjunto de variáveis de estado que
determinam completamente o
comportamento do sistema.
• Variáveis de estado:
• Especificado o estado inicial em 𝑡 = 𝑡0 e a
entrada para 𝑡 ≥ 𝑡0, determinam o
comportamento do sistema para 𝑡 ≥ 𝑡0.
3

4. Definições
• Vetor de estado:
• Possui como componentes as variáveis de
estado.
• Determinam o estado do sistema para
qualquer instante 𝑡 ≥ 𝑡0, dada a entrada e o
estado inicial.
• Espaço de estados:
• Espaço cujos eixos coordenados representam
as variáveis de estado (um eixo para cada
variável).
4

5. Análise no espaço de estados
• Envolve três tipos de variáveis:
• Variáveis de entrada;
• Variáveis de saída;
• Variáveis de estado.
• O sistema dinâmico deve conter elementos que
memorizem seus dados.
• Integradores, em um sistema de controle de
tempo contínuo , servem como dispositivos de
memória. Portanto, a saída desses integradores
podem ser consideradas variáveis de estado.
5

6. Análise no espaço de estados
• O número de variáveis de estado é igual ao
número de integradores.
• Supondo um sistema com:
• r entradas: 𝑢1 𝑡 , 𝑢2 𝑡 , … , 𝑢 𝑟 𝑡 ;
• m saídas: 𝑦1 𝑡 , 𝑦2 𝑡 , … , 𝑦 𝑚 𝑡 ;
• n variáveis de estado: 𝑥1 𝑡 , 𝑥2 𝑡 , … , 𝑥 𝑛 𝑡
6

7. Equações no espaço de estados
• O sistema pode ser escrito como:
𝑥1 𝑡 = 𝑓1(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
𝑥2 𝑡 = 𝑓2 𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡
⋮
𝑥 𝑛 𝑡 = 𝑓𝑛(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
𝑦1 𝑡 = 𝑔1(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
𝑦2 𝑡 = 𝑔2 𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡
⋮
𝑦 𝑚 𝑡 = 𝑔 𝑚(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡) 7

8. Equações no espaço de estados
• Definindo:
𝒙 𝑡 =
𝑥1(𝑡)
𝑥2(𝑡)
⋮
𝑥 𝑛(𝑡)
, 𝒚 𝑡 =
𝑦1(𝑡)
𝑦2(𝑡)
⋮
𝑦 𝑚(𝑡)
, 𝒖 𝑡 =
𝑢1(𝑡)
𝑢2(𝑡)
⋮
𝑢 𝑟(𝑡)
,
𝒇(𝒙, 𝒖, 𝑡) =
𝑓1(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
𝑓2(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
⋮
𝑓𝑛(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
,
𝒈(𝒙, 𝒖, 𝑡) =
𝑔1(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
𝑔2(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
⋮
𝑔 𝑚(𝑥1, 𝑥2, … , 𝑥 𝑛; 𝑢1, 𝑢2, … , 𝑢 𝑛; 𝑡)
,
8

9. Equações no espaço de estados
• Equação de estado:
𝒙 𝑡 = 𝒇 𝒙, 𝒖, 𝑡
• Equação de saída:
𝒚 𝑡 = 𝒈 𝒙, 𝒖, 𝑡
• Se as funções vetoriais 𝒇 ou 𝒈 envolverem
explicitamente o tempo t, então o sistema é
chamado de variante no tempo.
9

10. Equações no espaço de estados
• Se as equações forem linearizadas em torno de
um ponto de operação, temos:
𝒙 𝑡 = 𝑨 𝑡 𝒙 𝑡 + 𝑩 𝑡 𝒖(𝑡)
𝒚 𝑡 = 𝑪 𝑡 𝒙 𝑡 + 𝑫 𝑡 𝒖(𝑡)
• 𝑨 𝑡 é chamada de matriz de estado,
𝑩 𝑡 de matriz de entrada, 𝑪 𝑡 de matriz de
saída e 𝑫 𝑡 de matriz de transmissão direta.
10

11. Equações no espaço de estados
• Se as funções vetoriais 𝒇 ou 𝒈 não envolverem
explicitamente o tempo t, então o sistema é
chamado de invariante no tempo.
• Nesse caso, temos:
𝒙 𝑡 = 𝑨𝒙 𝑡 + 𝑩𝒖(𝑡)
𝒚 𝑡 = 𝑪𝒙 𝑡 + 𝑫𝒖(𝑡)
11

12. Equações no espaço de estados
• Exemplo:
• Admitimos que o sistema é linear.
• A força externa u(t) é a entrada.
• O deslocamento y(t) da massa m
é a saída.
• O deslocamento é medido a partir
da posição de equilíbrio, na
ausência da força externa.
12

13. Equações no espaço de estados
• Exemplo:
• Equação dinâmica do sistema:
𝑚𝑦 + 𝑏𝑦 + 𝑘𝑦 = 𝑢
• Sistema de segunda ordem, com
dois integradores e duas
variáves de estado:
𝑥1 𝑡 = 𝑦 𝑡
𝑥2 𝑡 = 𝑦(𝑡)
13

14. Equações no espaço de estados
• Equação de estado:
𝑥1 = 𝑥2
𝑥2 = −
𝑘
𝑚
𝑥1 −
𝑏
𝑚
𝑥2 +
1
𝑚
𝑢
• Equação de saída:
𝑦 = 𝑥1
• Diagrama de blocos:
14

15. Equações no espaço de estados
• Forma vetorial-matricial:
𝑥1
𝑥2
=
0 1
−
𝑘
𝑚
−
𝑏
𝑚
𝑥1
𝑥2
+
0
1
𝑚
𝑢
𝑦 = 1 0
𝑥1
𝑥2
15

16. Função de Transferência
• Podemos encontrar 𝐺 𝑠 =
𝑌(𝑠)
𝑈(𝑠)
para a equação
do espaço de estados, considerando um sistema
de entrada e saída únicas:
𝒙 𝑡 = 𝑨𝒙 𝑡 + 𝑩𝒖(𝑡)
𝑦 𝑡 = 𝑪𝒙 𝑡 + 𝐷𝑢(𝑡)
𝒔𝑿(𝑠) = 𝑨𝑿 𝑠 + 𝑩𝑈(𝑠)
𝑌 𝑠 = 𝑪𝑿 𝑠 + 𝐷𝑈 𝑠
16

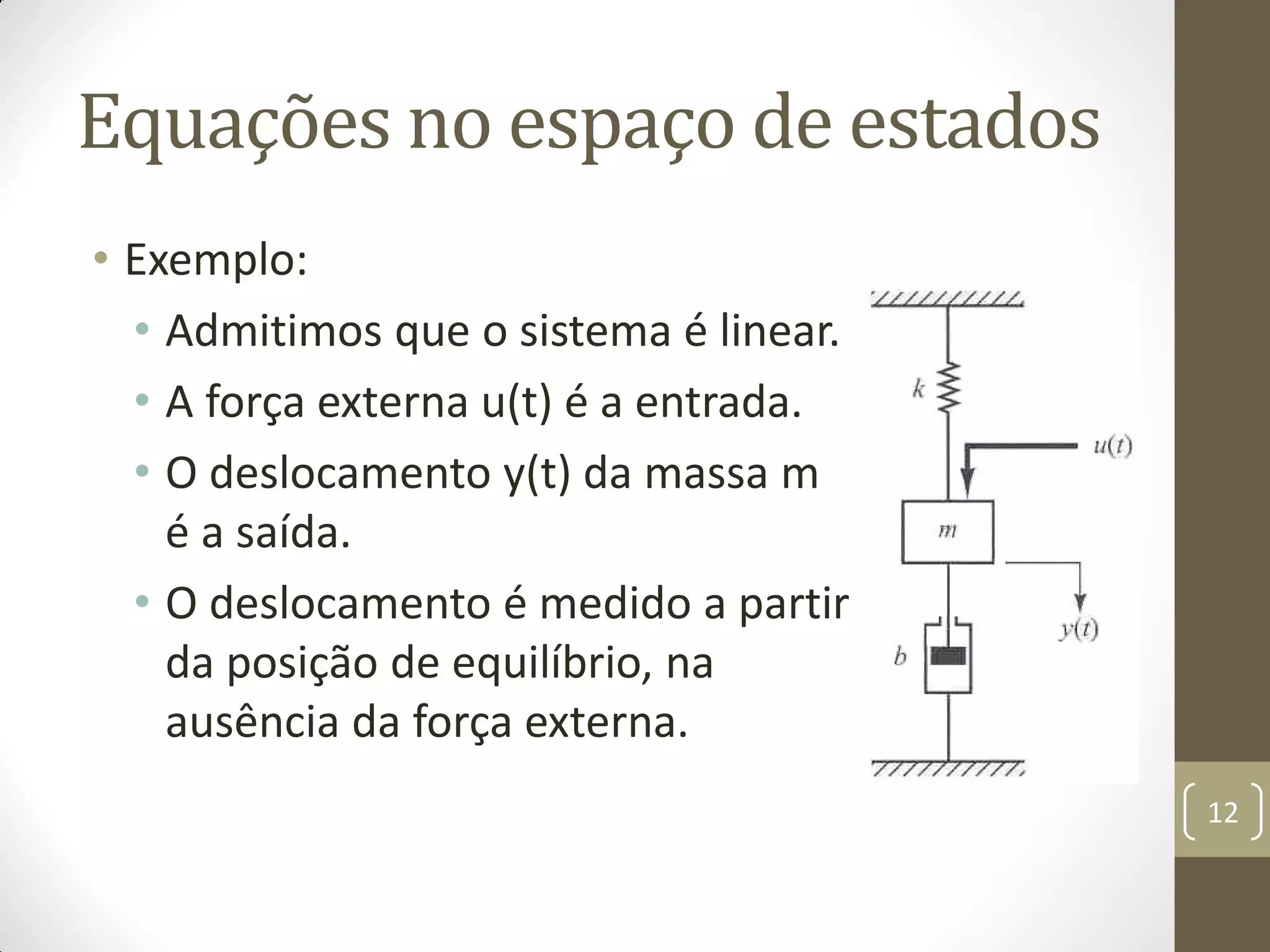
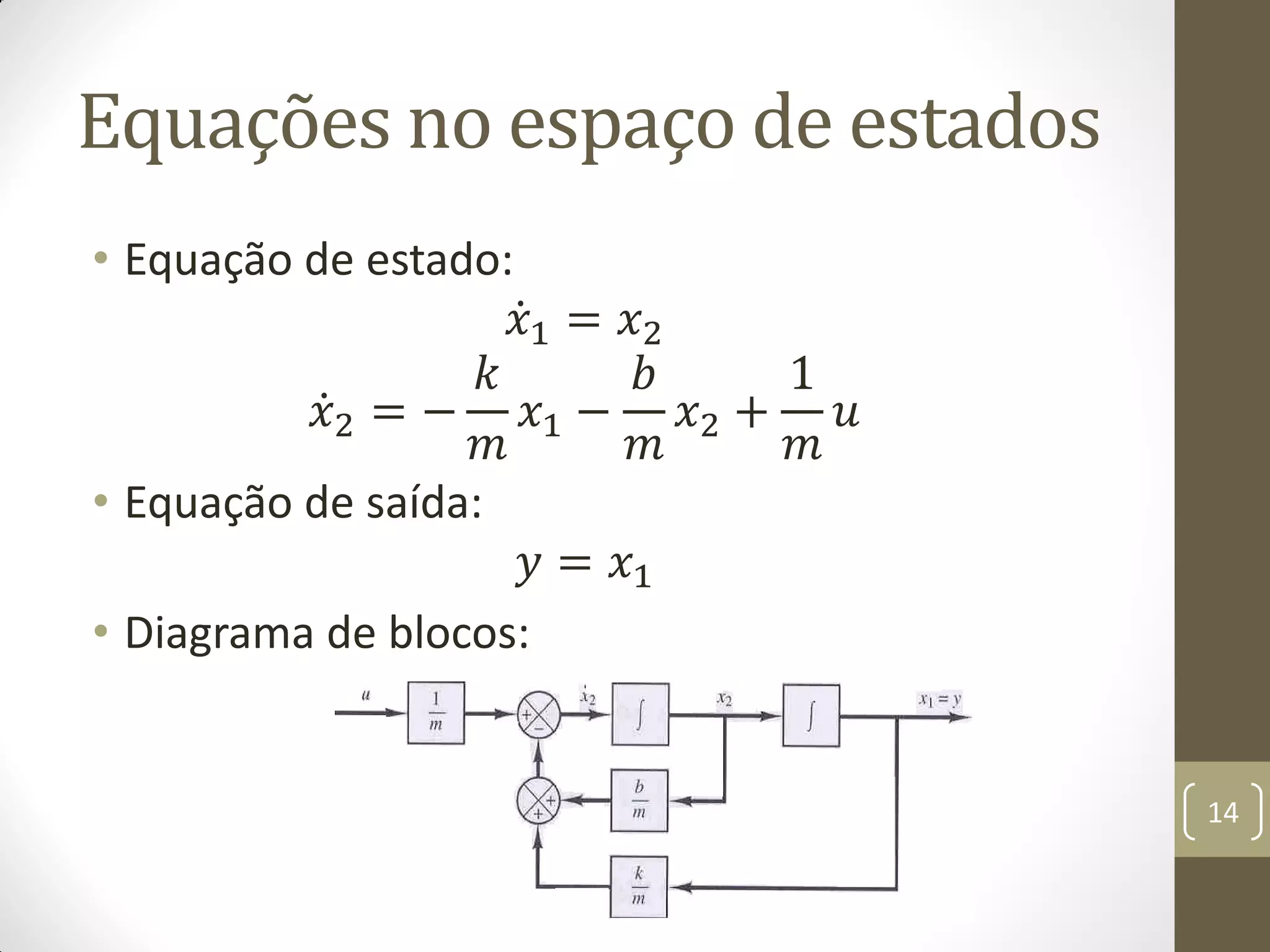
17. Função de Transferência
• Isolando 𝑿(𝑠):
𝒔𝑿 𝑠 − 𝑨𝑿 𝑠 = 𝑩𝑈(𝑠)
𝒔𝑰 − 𝑨 𝑿 𝑠 = 𝑩𝑈 𝑠
𝑿(𝑠) = 𝒔𝑰 − 𝑨 −1 𝑩𝑈(𝑠)
• Substituindo em 𝒀 𝑠 :
𝑌 𝑠 = 𝑪 𝒔𝑰 − 𝑨 −1 𝑩𝑈(𝑠) + 𝐷𝑈 𝑠
𝑌 𝑠 = [𝑪 𝒔𝑰 − 𝑨 −1 𝑩 + 𝐷]𝑈(𝑠)
𝐺 𝑠 =
𝑌(𝑠)
𝑈(𝑠)
= 𝑪 𝒔𝑰 − 𝑨 −1
𝑩 + 𝐷
17

18. Função de Transferência
• Exemplo:
• Considerando o sistema mecânico
anterior, podemos encontrar G(s):
𝐺 𝑠 = 𝑪 𝒔𝑰 − 𝑨 −1 𝑩 + 𝐷
𝐺 𝑠 = 1 0
𝑠 0
0 𝑠
−
0 1
−
𝑘
𝑚
−
𝑏
𝑚
−1
0
1
𝑚
𝐺 𝑠 = 1 0
𝑠 −1
𝑘
𝑚
𝑠 +
𝑏
𝑚
−1
0
1
𝑚
𝐺 𝑠 = 1 0
1
𝑠2 +
𝑏
𝑚
𝑠 +
𝑘
𝑚
𝑠 +
𝑏
𝑚
1
−
𝑘
𝑚
𝑠
0
1
𝑚
𝐺 𝑠 =
1
𝑚𝑠2 + 𝑏𝑠 + 𝑘
18

19. Matriz de Transferência
• Considerando um sistema com múltiplas
entradas e saídas:
𝑮 𝒔 =
𝒀(𝒔)
𝑼(𝒔)
= 𝑪 𝒔𝑰 − 𝑨 −1 𝑩 + 𝑫
• Como o vetor de entrada tem dimensão r e o
vetor de saída tem dimensão m, a matriz de
transferência terá dimensões m x r.
19

20. Obrigada!
ays@icmc.usp.br
www.lsec.icmc.usp.br
20