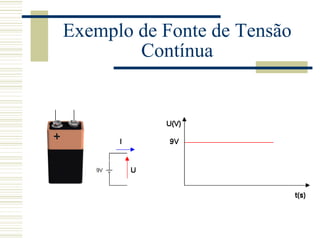
Este documento introduz os conceitos de tensão contínua e alternada, e descreve as características de tensões senoidais. Explica que uma tensão alternada varia com o tempo de acordo com uma função senoidal, e apresenta suas representações gráfica e matemática. Também aborda conceitos como frequência, período, valores de pico e eficaz de tensões e correntes alternadas.

1. Introdução a Corrente Alternada

2. Tensão Continua
Uma tensão é chamada de continua ou
constante quando o seu valor não se altera
com o tempo.
Exemplo de geradores que geram tensão
continua são as pilhas e as baterias.
A Figura a seguir mostra o aspecto físico,
símbolo e curva da tensão em função do
tempo deste tipo de gerador.

3. Exemplo de Fonte de Tensão
Contínua

4. Tensão Alternada
É uma tensão cujo valor e polaridade se
modificam ao longo do tempo. Conforme o
comportamento da tensão, temos os
diferentes tipos de tensão:
Senoidal, quadrada, triangular, pulsante,
etc.
De todas essas, analisaremos a partir de
agora a senoidal, porque é a tensão fornecida
nas fontes geradoras e que alimenta as
industrias e residências.

5. Tensão Alternada
Seja o circuito da próxima Figura, no qual
temos duas baterias e uma chave que ora
conecta a bateria B1 ao resistor, ora conecta
a bateria B2 ao resistor.
Vamos supor que cada
bateria fica conectada ao
resistor durante 1s.
Como seria o gráfico da
tensão em função do tempo nos
terminais da bateria ?

6. Exemplo de Geração Alternada
• O valor negativo significa que a polaridade da tensão mudou. Desta forma
obtemos uma forma de onda quadrada. Além desta, usualmente temos aplicações
em eletricidade as formas triangular e principalmente a senoidal.
• O tempo que leva para repetir uma mesma situação é 2s, sendo chamado de
período (T). O valor máximo da tensão é 12V ( sendo chamado de valor de pico
ou valor máximo VM). A seguir analisaremos mais em detalhes a senoidal.

7. Tensão Senoidal
É uma tensão que varia com o tempo de
acordo com uma função senoidal
A expressão matemática é dada pela função:
( ) . ( . )Mv t V sen tω θ= +
Onde VM é o valor de pico (valor máximo que a tensão
pode ter) , em (rad/s) é a freqüência angular e (rd ou
graus) é o angulo de fase inicial.

8. Representação Gráfica
VPP (em V) é chamado de tensão de pico a
pico, T (em s) é o período da função.

9. Representação gráfica de uma tensão
senoidal em função do angulo
A rotação da bobina ao longo de 360º geométricos( 1
rotação ) gera sempre 1 ciclo ( 360º) de Tensão (
Gerador de 2 pólos).

10. Corrente Alternada
Quando uma tensão senoidal é ligada aos terminais
de uma resistência de carga, a corrente também é
uma onda senoidal.

11. Exemplo
Exemplo 1:
Uma tensão senoidal ca é
aplicada a uma resistência
de carga de 10 . Mostre a
onda senoidal resultante
para a corrente alternada.
O valor máximo da corrente é
10
1
10
M
M
V
I A
R
= = =
O Valor instantâneo da
corrente é i=v/R. Num
circuito apenas com
resistência, a forma de onda
da corrente segue a
polaridade da forma de onda
da tensão.
Graficamente, é representado por:
Como a corrente é definida
pela expressão:
.Mi I senθ=

12. Freqüência e Período
O número de ciclos por minuto é chamado de Freqüência.
É representada pela letra f e unidade em hertz [Hz].
O intervalo de tempo para que um ciclo se complete é chamado de período.
É representado pelo símbolo T e expresso em segundos [s].
A freqüência é o recíproco do período, ou seja:
1 1
f e T
T f
= =
Quanto maior a freqüência,
menor o período.

13. Relação entre graus
elétricos e tempo
O ângulo de 360º representa o tempo para um ciclo,
ou período T.
Portanto, temos a seguinte representação gráfica.

14. Exemplo
Exemplo 2
Uma corrente ca varia ao longo de um ciclo completo em 1/100s. Qual
o período e a freqüência? Se a corrente tiver um valor máximo de 5A,
mostre a forma de onda para a corrente em graus e em segundos.
1
10 10
100
T s ou ms ou ms=
1 1
100
1/100
f Hz
T
= = =
Graficamente

15. Relações de Fase
O ângulo de fase entre duas formas de onda de mesma freqüência é a
diferença angular num dado instante.
Na figura abaixo, o ângulo de fase entre as ondas B e A é de 90º
Enquanto a onda A começa com seu valor máximo e cai para zero em
90º.
A onda B atinge o seu valor máximo 90º na frente de A.
Este ângulo de fase de 90º entre as ondas B e A é mantido durante o
ciclo completo e todos os ciclos sucessivos.

16. Fasores
Forma alternativa para representação de correntes e tensões
alternadas (senoidais).
Um fasor é uma entidade com módulo e sentido.
O comprimento do fasor representa o módulo da
tensão/corrente alternada.
O ângulo em relação ao eixo horizontal indica ao ângulo de fase.

17. Representação Fasorial
Tomando com exemplo a figura abaixo, o fasor VA representa a
onda de tensão A com ângulo de fase de 0º.
O fasor VB é vertical para mostrar o ângulo de fase de 90º com
relação ao fasor VA, que serve de referência.

18. Representação Fasorial
Quando duas ondas estão em fase, o ângulo de fase é
zero. As amplitudes se somam.
Quando as ondas estão exatamente fora de fase, o
ângulo de fase é de 180º. Suas amplitudes são
opostas.

19. Exemplo
Exemplo 3
Qual o ângulo de fase entre as ondas A e B? Faça o diagrama de fasores primeiro
com a onda A como referência e depois como a onda B como referência.
Ângulo de fase é a distância angular entre pontos
correspondentes nas ondas A e B.
Os pontos correspondentes mais convenientes sâo os pontos
de máximo, dos mínimos e dos zeros de cada onda.
A como referência B como referência
No cruzamento dos zeros no eixo horizontal, =30º.

20. Valores Características de
Tensão e de Corrente
Valor de pico é o valor máximo VMax ou IMax.
Valor de pico a pico é igual ao dobro do valor de pico, quando os picos positivo e
negativo são simétricos.
Valor médio, corresponde à média aritmética de todos os valores numa onda
senoidal, considerando um meio ciclo.
ValorMedio 0,637
0,6237.
0,637.
M Max
M Max
xvalor de pico
V V
I I
=
=
=
O valor rms de uma onda senoidal corresponde à mesma quantidade de tensão
ou corrente contínua capaz de produzir a mesma potência dissipada.
O valor eficaz ou rms ou valor médio quadrático corresponde a 0,707 vezes o
valor de pico.
Valorrms 0,707
0,707.
0,707.
M Max
M Max
xvalor de pico
V V
I I
=
=
=

21. Valores Características de
Tensão e de Corrente

22. Resistência em Circuitos CA
Em circuitos ca somente com resistência.
Tensão e Corrente estão em fase.
Esta relação entre V e I em fase, significa que este circuito ca
pode ser analisado pelos métodos usados para o circuito cc.
Seja o circuito, abaixo, em série.
2 2110
11 . 11 .10 1210
10
V
I A P I R W
R
= = = = = =

23. Exercício
45o
45o
Exercício 1
Calcule o ângulo
de fase para as
seguintes ondas
ca e desenhe os
respectivos
diagramas de
fasores

24. Exercício

25. Indutância, Reatância e
Circuitos Indutivos
A capacidade de um condutor possui de induzir tensão em si
mesmo quando a corrente varia é chamada de auto-indutância
ou simplesmente indutância.
lv
L
i
t
=
∆
∆
Onde: L= indutância, [H]
v= tensão induzida através da bobina, [V]
i/ t= taxa de variação da corrente, [A/s]

26. Indutância Mútua
Quando a corrente num condutor ou numa bobina varia, este
fluxo pode interceptar qualquer outro condutor ou bobina nas
vizinhanças, induzindo tensões em ambos.

27. Características das Bobinas
A indutância de uma bobina depende de como ela é enrolada, material
do núcleo em torno do qual é enrolada, e do número de espiras que
formam o enrolamento.
A indutância L aumenta com o número de espiras N em torno do núcleo. A
indutância aumenta com o quadrado do número de espiras.
A indutância aumenta com a permeabilidade relativa r do material de que
é feito o núcleo.
À medida que a área A abrangida em cada espira aumenta. A indutância
aumenta com o quadrado do diâmetro.
A indutância diminui à medida que o comprimento da bobina aumenta.
( )
2
6.
. 1,26 10 ,[ ]r
N A
L x H
l
µ −
=

28. Reatância Indutiva
Onde XL= reatância indutiva,[ ]
f = freqüência angular,[Hz]
L = indutância, [Hz]
2. . .LX f Lπ=
A reatância indutiva XL é a oposição à corrente ca
devida à indutância do circuito.
A unidade da reatância indutiva é o ohm.
A fórmula para a reatância indutiva é

29. Indutores em série
Se os indutores forem dispostos afastados um do outro de modo
que não interajam eletromagneticamente entre si.
Podem ser associados como resistores.
1 2 3 ........T nL L L L L= + + + +
1 2 2.T ML L L L= + ±
Se duas bobinas ligadas em série
forem colocadas próximas de modo
que linhas de campo magnético se
interliguem.
A indutância total será:

30. Indutores em paralelo
Afastados, de modo que a indutância mútua seja
desprezível, tem-se que:
1 2 3
1 1 1 1 1
........
T nL L L L L
= + + + +
No caso de apenas duas bobinas em paralelo, tem-se
que:
1 2
1 2
.
T
L L
L
L L
=
+

31. Circuitos Indutivos
Seja uma tensão ca, v, aplicada a um circuito que tenha
somente indutância.
A corrente iL, que passa pela indutância estará atrasada da
tensão vL, de 90º.

32. Circuito RL em série
Quando uma bobina têm uma resistência em série, a corrente I é
limitada tanto por XL quanto por R.
A corrente I , através de XL, está defasada da tensão VL de 90º.
. .R L LV I R e V I X= =

33. Exemplo
Exemplo 4
Um circuito ca com RL em série tem uma corrente de 1A de pico, com R=50 e XL=50
.
Calcule VR, VL, VT e . Faça o diagrama de fasores de VT e I. Faça também o diagrama
de tempo i, vR, vL e vT.

34. Impedância RL série
A resultante da adição dos fasores R e XL é chamada de
impedância. É representada pelo símbolo Z.
A impedância é a reação total ao fluxo da corrente em ohms [ ].
2 2 2
T R LV V V= +
( ) ( ) ( )
2 2 2
. . . LI Z I R I X= +
2 2
LZ R X= +
L LX X
tg arctg
R R
θ θ= → =
2 2 2
LZ R X= +

35. Circuito RL paralelo
Para circuitos paralelo contendo R e XL , uma mesma tensão VT
está aplicada a eles.
Portanto esta tensão será usada como referência.

36. Exemplo

37. Impedância RL paralelo
Cálculo a partir da tensão como referência.
Exemplo: Qual a impedância de ZT de um R de 200 em paralelo
com XL de 400 ? Suponha que a tensão VT seja de 400 V.
400
2
200
T
R
V
I A
R
= = =
400
1
400
T
L
L
V
I A
X
= = =
2 2
4 1 5 2,24T R LI I I A= + = + = =
400
178,6
2,24
T
T
T
V
Z
I
= = = Ω

38. Potência em circuitos RL
Num circuito ca com reatância indutiva, a corrente está
atrasada em relação a tensão aplicada.
Existe neste caso 3 tipos de potência.
. ( .cos ) cosPot real P V I VIθ θ= =
. ( . )Pot reativa Q V I sen VIsenθ θ= =
.Pot aparente S VI=
Tensão e corrente expressos em valor rms.

39. Exemplo
Exemplo 6
O circuito ca tem 2A através de um R de 173 Ω em série com um XL de 100
Ω. Calcule o fator de potência, a tensão aplicada V, a potência real P, a
potência reativa Q e a potência aparente S.
100
0,578 30
173
cos cos30 0,866
173
200
cos cos30º
oL
o
X
arctg arctg arctg
R
FP
R
Z
θ
θ
θ
= = = =
= = =
= = = Ω
. 2(200) 400V I Z V= = = . . 400.(2).( 30º) 400
. 400.(2) 600
Q V I sen sen VAr
S V I VA
θ= = =
= = =
2 2
2 .(173) 692
. .cos 400.(2).(cos30º) 692
P I R W
ou
P V I Wθ
= = =
= = =

40. Capacitância, Reatância
Capacitiva e Circuitos Capacitivos
Um capacitor é um dispositivo elétrico
formado por duas placas condutoras de metal
separadas por um material isolante chamado
dielétrico.

41. Capacitância
O capacitor armazena carga elétrica no dielétrico.

42. Capacitância
Capacitância
Capacidade de armazenamento de carga elétrica.
Quantidade de carga que pode ser armazenada num
capacitor dividida pela tensão aplicada às placas.
Q
C
V
=
Onde C=capacitância,F
Q= quantidade de carga,C
V=tensão,V

43. Capacitores em série e em
paralelo
Associação série.
1 2 3
1 1 1 1 1
...................
T nC C C C C
= + + +
Associação paralelo.
1 2 3 ...................T nC C C C C= + + +

44. Reatância Capacitiva
A reatância capacitiva XC é a oposição
ao fluxo de corrente.
Unidade: [ohm] ou [ ].
1 1 0,159
2. . . 6,28. . .
CX
f C f C f Cπ
= = =
Onde XC = reatância capacitiva,
f = freqüência, Hz
C = capacitância, F

45. Circuitos Capacitivos
Somente Capacitância.

46. Circuitos RC Série
A associação da resistência com a reatância
capacitiva é chamada de impedância.
2 2 2
T R CV V V= + C C
R R
V V
tg arctg
V V
θ θ
 
= − → = − 
 

47. Exemplo
Exemplo 7. Um circuito ca RC em série tem uma
corrente de pico de 1 A com R=50 e XC=120 .
Calcule VR, VC, VT e . Faça o diagrama de fasores