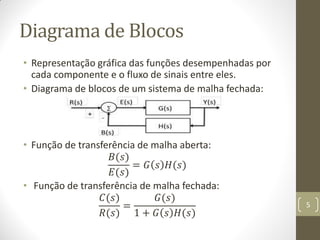
1) A Transformada de Laplace é um método operacional para solucionar equações diferenciais lineares através de simplificações. 2) Funções de transferência caracterizam as relações de entrada e saída de sistemas, geralmente representadas por equações diferenciais lineares invariantes no tempo. 3) O espaço de estados define o estado mínimo de variáveis que determinam completamente o comportamento de um sistema através de equações de estado e saída.