1. O documento apresenta um resumo de um livro sobre controle de sistemas em tempo contínuo.
2. O livro aborda tópicos como transformada de Laplace, modelagem de sistemas, análise de estabilidade e projeto de controladores.
3. O autor escreveu o livro com base em suas aulas e espera que ele sirva como um guia de estudos útil para alunos interessados no assunto.









![Controle de Sistemas em Tempo Cont´ınuo
por opera¸c˜oes alg´ebricas no plano complexo. A componente transit´oria e a
de regime permanente podem ser obtidas simultaneamente. Al´em disso, a
transformada de Laplace ´e fundamental para a an´alise de sistemas via fun¸c˜oes
de transferˆencia.
A transformada de Laplace de uma fun¸c˜ao f(t) ´e definida por
F(s) = L [f(t)] =
∞
0
f(t)e−st
dt, com s = σ + jw.
A transformada inversa de Laplace ´e dada por
f(t) = L−1
F(s) =
1
2πj
σ+j∞
σ−j∞
F(s)est
ds, t > 0.
A integral de Laplace existir´a/convergir´a se σ0 ´e escolhido de forma que
lim
t→∞
e−σ0t
f(t) = 0, (1)
onde σ0 ´e chamado de abscissa de convergˆencia.
Para a maioria das fun¸c˜oes ´e poss´ıvel adotar um valor de σ0 positivo
e suficientemente grande tal que a equa¸c˜ao (1) ´e satisfeita. Isso sempre
ser´a verdadeiro para exponenciais positivas ou para fun¸c˜oes que crescem a
uma taxa menor que uma exponencial. Existem fun¸c˜oes onde isso n˜ao ser´a
satisfeito para nenhum valor de σ0, por exemplo, et2
, que por sorte aparecem
raramente nos problemas de engenharia.
Exemplo: Calcular L[f(t)] para f(t) = e−at
, a = b + jc.
F(s) = L e−at
=
∞
0
e−at
e−st
dt =
=
∞
0
e−(s+a)t
dt =
−1
s + a
e−(s+a)t
∞
0
=
−1
s + a
[0 − 1] =
1
s + a
.
A abscissa de convergˆencia ´e determinada por
lim
t→∞
e−σ0t
e−at
= lim
t→∞
e−(σ0+b+jc)t
= lim
t→∞
e−(σ0+b)t
e−jct
,
e para que este limite convirja a zero, ent˜ao σ0 + b > 0, ou σ0 > −b.
Exemplo: Calcular L[f(t)] para f(t) = cos(wt).
´E poss´ıvel escrever que
cos(wt) =
1
2
ejwt
+ e−jwt
.
Prof. Dr. Alberto Luiz Serpa - 2009 12](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-12-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
Logo,
L[f(t)] =
1
2
L[ejwt
] + L[e−jwt
] =
1
2
1
s − jw
+
1
s + jw
=
s
s2 + w2
.
lim
t→∞
e−σ0t 1
2
e−jwt
+ e−jwt
= 0, se σ0 > 0.
Exemplo: Calcular L[u(t)] para o degrau unit´ario u(t).
u(t) =
0 se t ≤ 0,
1 = e0t
se t > 0.
Logo,
U(s) = L[u(t)] =
1
s + 0
=
1
s
, σ0 > 0.
Exemplo: Calcular L[δ(t)] para o impulso unit´ario δ(t).
Seja a fun¸c˜ao f(t) mostrada na Figura 10 e definida por
f(t) =
0 se t < 0,
1
t0
se 0 ≤ t ≤ t0,
0 se t0 < t.
f(t)
t
1
t0
t0
Figura 10: Representa¸c˜ao do impulso unit´ario, t0 → 0.
O impulso unit´ario pode ser representado como:
δ(t) = lim
t0→0
f(t).
Prof. Dr. Alberto Luiz Serpa - 2009 13](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-13-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
Assim,
L[δ(t)] = L lim
t0→0
f(t) =
∞
0
lim
t0→0
f(t)e−st
dt =
= lim
t0→0
∞
0
f(t)e−st
dt = lim
t0→0
t0
0
1
t0
e−st
dt =
= lim
t0→0
1
t0
−1
s
e−st
t0
0
= lim
t0→0
1 − e−st0
st0
.
Aplicando a regra de L’Hopital tem-se que
lim
t0→0
1 − e−st0
st0
= lim
t0→0
s e−st0
s
= 1.
Portanto,
L[δ(t)] = 1.
3.1 Propriedades da Transformada de Laplace
3.1.1 Linearidade
A transformada de Laplace ´e um operador linear, ou seja,
L[α1f1 + α2f2] = α1L(f1) + α2L(f2).
Prova:
L[α1f1 + α2f2] =
∞
0
(α1f1 + α2f2)e−st
dt =
∞
0
α1f1e−st
dt +
∞
0
α2f2e−st
dt = α1L[f1] + α2L[f2].
3.1.2 Diferencia¸c˜ao real
Se
L[f(t)] = F(s),
ent˜ao,
L
df
dt
= sF(s) − f(0).
Prova:
L
df
dt
=
∞
0
df
dt
e−st
dt =
∞
0
e−st
df.
Prof. Dr. Alberto Luiz Serpa - 2009 14](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-14-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
Integrando por partes, udv = uv − vdu, com u = e−st
, dv = df,
du = −se−st
dt e v = f(t), tem-se,
∞
0
udv = e−st
f(t)|∞
0 −
∞
0
f(t)(−s)e−st
dt =
= e−st
f(t)|∞
0 +
∞
0
f(t)s e−st
dt = 0 − f(0) + sF(s).
Portanto,
L
df
dt
= sF(s) − f(0).
Generalizando, tem-se:
L
dn
f(t)
dtn
= sn
F(s) −
n−1
i=0
sn−i−1 di
f
dti
t=0
.
Prova:
Seja g = df
dt
. Logo,
L
dg
dt
= sG(s) − g(0) = sL[g(t)] − g(0) =
= sL
df
dt
− g(0) = s(sF(s) − f(0)) −
df
dt t=0
=
= s2
F(s) − sf(0) −
df
dt t=0
.
Seja h = dg
dt
. Logo,
L
dh
dt
= sH(s) − h(0) = sL[h(t)] − h(0) =
= sL
dg
dt
− h(0) = s(sG(s) − g(0)) − h(0) =
= s2
G(s) − sg(0) − h(0) = s2
L[g(t)] − sg(0) − h(0) =
= s2
L
df
dt
− s
df
dt t=0
−
d2
f
dt2
t=0
=
= s2
(sF(s) − f(0)) − s
df
dt t=0
−
d2
f
dt2
t=0
=
Prof. Dr. Alberto Luiz Serpa - 2009 15](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-15-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
= s3
F(s) − s2
f(0) − s
df
dt t=0
−
d2
f
dt2
t=0
.
Pode-se continuar assim por diante para derivadas de ordem n.
Se todas as condi¸c˜oes iniciais s˜ao nulas tem-se que:
L
dn
f(t)
dtn
= sn
F(s).
Note que derivar no tempo corresponde a multiplicar por s no dom´ınio
de Laplace quando as condi¸c˜oes iniciais s˜ao nulas.
3.1.3 Integra¸c˜ao real
Se L[f(t)] = F(s), ent˜ao,
L f(t)dt =
1
s
F(s) +
1
s
f(t)dt
t=0
Quando todas as condi¸c˜oes iniciais s˜ao nulas tem-se que:
L f(t)dt =
F(s)
s
.
Prova:
L f(t)dt =
∞
0
f(t)dt
u
e−st
dt
dv
Definindo-se u = f(t)dt e dv = e−st
dt tem-se que v = e−st
−s
, o que permite
fazer uma integra¸c˜ao por partes ( udv = uv − vdu). Logo,
∞
0
f(t)dt e−st
dt =
e−st
−s
f(t)dt
∞
0
−
∞
0
e−st
−s
f(t)dt =
=
1
s
f(t)dt
t=0
+
1
s
∞
0
f(t)e−st
dt =
=
1
s
F(s) +
1
s
f(t)dt
t=0
= L f(t)dt .
Note que integrar no tempo corresponde a dividir por s no dom´ınio de
Laplace quando as condi¸c˜oes iniciais s˜ao nulas.
Prof. Dr. Alberto Luiz Serpa - 2009 16](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-16-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
3.1.4 Teorema do valor final
Se L[f(t)] = F(s) e existirem
L
df
dt
, lim
t→∞
f(t) e lim
s→0
sF(s),
ent˜ao,
lim
t→∞
f(t) = lim
s→0
sF(s).
Prova:
L
df
dt
= sF(s) − f(0) ⇒ L
df
dt
+ f(0) = sF(s),
lim
s→0
sF(s) = lim
s→0
L
df
dt
+ f(0) = lim
s→0
L
df
dt
+ f(0) =
= lim
s→0
∞
0
df
dt
e−st
dt + f(0) =
∞
0
lim
s→0
e−st
df + f(0) =
∞
0
df + f(0) = f(∞) − f(0) + f(0) = f(∞) = lim
t→∞
f(t).
3.1.5 Teorema do valor inicial
Se L[f(t)] = F(s) e existirem
L
df
dt
e lim
s→∞
sF(s),
ent˜ao,
lim
t→0+
f(t) = lim
s→∞
sF(s).
Prova:
lim
s→∞
sF(s) = lim
s→∞
L
df
dt
+ f(0) = lim
s→∞
L
df
dt
+ f(0) =
= lim
s→∞
∞
0
df
dt
e−st
dt + f(0) =
∞
0
lim
s→∞
e−st
df + f(0) = f(0) = lim
t→0+
f(t).
Prof. Dr. Alberto Luiz Serpa - 2009 17](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-17-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
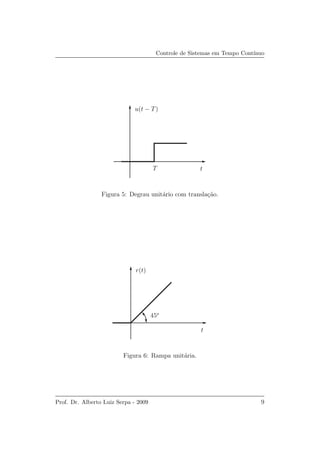
f(t) f(t − T)u(t − T)
tT
Figura 11: Representa¸c˜ao da transla¸c˜ao de f(t).
3.1.6 Transla¸c˜ao real
Seja F(s) = L[f(t)], ent˜ao,
L[f(t − T)u(t − T)] = e−sT
F(s).
Prova:
L [f(t − T)u(t − T)] =
∞
0
f(t − T)u(t − T)e−st
dt =
=
∞
T
f(t − T)u(t − T)e−st
dt =
∞
0
f(τ)u(τ)e−s(τ+T)
dτ =
= e−sT
∞
0
f(τ)u(τ)e−sτ
dτ = e−sT
F(s),
onde τ = t − T e dτ = dt.
t
T
τ
Figura 12: Representa¸c˜ao dos eixos t e τ.
3.1.7 Fun¸c˜oes peri´odicas
Para f(t) uma fun¸c˜ao peri´odica de per´ıodo T tem-se que
L[f(t)] =
1
1 − e−sT
F1(s),
Prof. Dr. Alberto Luiz Serpa - 2009 18](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-18-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
onde F1(s) = L[f1(t)] e f1(t) ´e o primeiro per´ıodo de f(t).
Prova:
f(t) = f1(t)u(t) + f1(t − T)u(t − T) + f1(t − 2T)u(t − 2T) + . . . ,
F(s) = L[f(t)] = L[f1(t)u(t)]+L[f1(t−T)u(t−T)]+L[f1(t−2T)u(t−2T)]+. . .
Mas
L[f1(t)u(t)] = F1(s),
L[f1(t − T)u(t − T)] = e−sT
F1(s),
L[f1(t − 2T)u(t − 2T)] = e−s2T
F1(s),
e conseq¨uentemente,
F(s) = F1(s) + e−sT
F1(s) + e−2sT
F1(s) + . . . = (1 + e−sT
+ e−2sT
+ . . .)F1(s).
Como T > 0 tem-se que e−sT
= 1
esT < 1. A seq¨uˆencia 1, 1
esT , 1
e2sT , ..., ´e
uma PG de raz˜ao 1
esT , cuja soma ´e 1
1−e−sT . Logo,
F(s) =
1
1 − e−sT
F1(s).
Verifica-se que o fato de s ser complexo n˜ao altera o resultado da PG, ou
seja,
1
esT
=
1
e(a+jb)T
=
1
eaT ejbT
,
onde eaT
> 1 e ejbT
´e peri´odico e limitado.
3.1.8 Diferencia¸c˜ao Complexa
Se L[f(t)] = F(s) ent˜ao
−
dF(s)
ds
= L[tf(t)].
Prova:
−
dF(s)
ds
= −
d
ds
∞
0
f(t)e−st
dt = −
∞
0
d
ds
f(t)e−st
dt =
= −
∞
0
f(t) −te−st
dt =
∞
0
tf(t)e−st
dt = L[tf(t)].
Prof. Dr. Alberto Luiz Serpa - 2009 19](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-19-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
3.1.9 Integra¸c˜ao Complexa
Se L[f(t)] = F(s), e existe ∞
s F(s)ds, ent˜ao,
L
f(t)
t
=
∞
s
F(s)ds.
Prova:
∞
s
F(s)ds =
∞
s
∞
0
f(t)e−st
dtds =
∞
0
f(t)
∞
s
e−st
ds dt =
=
∞
0
f(t)
−e−st
t
∞
s
dt =
∞
0
f(t)
t
e−st
dt = L
f(t)
t
.
3.1.10 Transla¸c˜ao Complexa
Se L[f(t)] = F(s), ent˜ao,
F(s + a) = L[e−at
f(t)].
Prova:
L[e−at
f(t)] =
∞
0
e−at
f(t)e−st
dt =
=
∞
0
f(t)e−(a+s)t
dt =
∞
0
f(t)e−¯st
dt = F(¯s) = F(s + a).
3.1.11 Convolu¸c˜ao Real
Define-se a convolu¸c˜ao entre f(t) e g(t) como
h(t) = f(t) ∗ g(t) =
t
0
f(τ)g(t − τ)dτ.
Se L[f(t)] = F(s) e L[g(t)] = G(s), ent˜ao,
L[f(t) ∗ g(t)] = F(s)G(s).
Prova:
t
0
f(τ)g(t − τ)dτ =
∞
0
f(τ)g(t − τ)u(t − τ)dτ,
pois
u(t − τ) = u(−(τ − t)) =
1 se −(τ − t) > 0 ou τ < t,
0 se −(τ − t) ≤ 0 ou τ ≥ t.
Prof. Dr. Alberto Luiz Serpa - 2009 20](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-20-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
t τ
Figura 13: Representa¸c˜ao de u(t − τ).
Seja H(s) = L[h(t)]. Logo, escreve-se:
H(s) = L[h(t)] =
∞
0
∞
0
f(τ)g(t − τ)u(t − τ)dτ e−st
dt =
=
∞
0
f(τ)
∞
0
g(t − τ)u(t − τ)e−st
dt dτ =
=
∞
0
f(τ) e−sτ
G(s) dτ = G(s)
∞
0
f(τ)e−sτ
dτ = G(s)F(s).
No caso de sistemas antecipativos e entradas para t < 0, deve-se estender
os limites de integra¸c˜ao, ou seja, h(t) = f(t) ∗ g(t) = ∞
−∞ f(τ)g(t − τ)dτ.
Contudo, esta situa¸c˜ao n˜ao ´e coberta neste material.
Exemplo: Calcular a transformada de Laplace da fun¸c˜ao dente de serra,
como ilustrada na Figura 14.
O primeiro per´ıdo desta fun¸c˜ao pode ser constru´ıdo atrav´es da soma de
trˆes termos conforme mostrado na Figura 14, ou ainda,
f1(t) =
A
T
[tu(t) − (t − T)u(t − T) − Tu(t − T)] .
Aplicando a transformada de Laplace a cada um destes termos tem-se:
L[tu(t)] = L u(t)dt =
1
s
U(s) + 0 =
1
s
1
s
=
1
s2
,
L[(t − T)u(t − T)] = e−sT 1
s2
,
L[Tu(t − T)] = Te−sT 1
s
.
Portanto, a transformada de Laplace do primeiro per´ıodo da fun¸c˜ao ´e:
F1(s) =
A
T
1
s2
−
e−sT
s2
−
Te−sT
s
.
Prof. Dr. Alberto Luiz Serpa - 2009 21](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-21-320.jpg)

![Controle de Sistemas em Tempo Cont´ınuo
2. Calcular as constantes ci, i = 1, . . ., n.
3. Obter a transformada inversa de cada fra¸c˜ao parcial, que s˜ao fun¸c˜oes
mais simples.
Exemplo: Caso de ra´ızes simples. Seja
X(s) =
a + bs
(s − µ1)(s − µ2)
; µ1 = µ2.
Pode-se escrever X(s) da seguinte forma:
X(s) =
a + bs
(s − µ1)(s − µ2)
=
c1
s − µ1
+
c2
s − µ2
onde c1 e c2 s˜ao constantes que devem ser determinadas.
Multiplicando-se por s − µ1 tem-se:
(s − µ1)X(s) =
a + bs
s − µ2
= c1 + (s − µ1)
c2
s − µ2
.
Fazendo s = µ1, pois s pode assumir qualquer valor, tem-se
(s − µ1)X(s)|s=µ1
= c1 =
a + bµ1
µ1 − µ2
.
De forma an´aloga
c2 = (s − µ2)X(s)|s=µ2
=
a + bµ2
µ2 − µ1
.
Logo,
X(s) =
a + bµ1
µ1 − µ2
1
s − µ1
+
a + bµ2
µ2 − µ1
1
s − µ2
.
A anti-transformada de cada fra¸c˜ao parcial pode ser calculada, ou seja,
f(t) = L−1
[X(s)] =
a + bµ1
µ1 − µ2
eµ1t
+
a + bµ2
µ2 − µ1
eµ2t
.
Portanto, para n ra´ızes simples tem-se que:
ci = (s − µi)X(s)|s=µi
, i = 1, 2, . . ., n.
Prof. Dr. Alberto Luiz Serpa - 2009 23](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-23-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
Exemplo: Ra´ızes M´ultiplas. Seja
X(s) =
a + bs
(s − µ1)2(s − µ2)
,
com µ1 de multiplicidade 2.
A expans˜ao em fra¸c˜oes parciais torna-se
X(s) =
a + bs
(s − µ1)2(s − µ2)
=
c1
(s − µ1)2
+
c2
(s − µ1)
+
c3
(s − µ2)
. (2)
Multiplicando por (s − µ1)2
obt´em-se
(s − µ1)2
X(s) =
a + bs
s − µ2
= c1 + (s − µ1)c2 +
(s − µ1)2
s − µ2
c3, (3)
e fazendo s = µ1, tem-se que
c1 =
a + bµ1
µ1 − µ2
.
Derivando a equa¸c˜ao (3) com rela¸c˜ao a s e fazendo s = µ1 obt´em-se c2,
ou seja,
c2 =
d
ds
(s − µ1)2
X(s)
s=µ1
=
d
ds
a + bs
s − µ2 s=µ1
=
−µ2b − a
(µ1 − µ2)2
.
Portanto, para q ra´ızes reais e iguais, s = µi, tem-se
cp =
1
(p − 1)!
dp−1
dsp−1
[(s − µi)q
X(s)]
s=µi
, p = 1, . . . , q.
Multiplicando a equa¸c˜ao (2) por s − µ2 e fazendo s = µ2 tem-se
a + bs
(s − µ1)2
s=µ2
= c3 ⇒ c3 =
a + bµ2
(µ2 − µ1)2
.
A anti-transformada de cada fra¸c˜ao parcial pode ser calculada como
L−1 1
(s − µi)q
=
1
(q − 1)!
tq−1
eµit
.
Exemplo: Determinar a transformada de Laplace de uma equa¸c˜ao de se-
gunda ordem
¨y + 2ξwn ˙y + w2
ny(t) = γw2
nf(t),
Prof. Dr. Alberto Luiz Serpa - 2009 24](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-24-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
com as seguintes condi¸c˜oes iniciais y(0) = y0 e ˙y(0) = v0.
Pode-se escrever
L[y(t)] = Y (s), L[ ˙y(t)] = sY (s) − y0 e L[¨y(t)] = s2
Y (s) − sy0 − v0.
Consequentemente
(s2
+ 2ξwns + w2
n)Y (s) − (s + 2ξwn)y0 − v0 = γw2
nF(s),
ou ainda
Y (s) =
1
s2 + 2ξwns + w2
n
γw2
nF(s) + v0 + (s + 2ξwn)y0 ,
onde cada termo desta equa¸c˜ao pode ser analizado de forma independente
devido ao sistema ser linear.
Com condi¸c˜oes iniciais nulas, y0 = 0 e v0 = 0, tem-se
Y (s) =
γw2
n
s2 + 2ξwns + w2
n
F(s) = G(s)F(s),
onde
G(s) =
γw2
n
s2 + 2ξwns + w2
n
´e a fun¸c˜ao de transferˆencia que relaciona a entrada `a sa´ıda do sistema e que
pressup˜oe condi¸c˜oes iniciais nulas, ou seja,
Y (s) = G(s)F(s).
Exemplo: Seja um sistema de primeira ordem descrito por
a1
dy
dt
+ a0y = b0x ⇒ τ
dy
dt
+ y = γx(t).
onde
τ =
a1
a0
e γ =
b0
a0
com a condi¸c˜ao inicial y(0) = 0.
Aplicando a transformada de Laplace, tem-se que
L τ
dy
dt
+ y = L[γx(t)] ⇒ τsY (s) + Y (s) = γX(s)
onde L[y(t)] = Y (s) e L[x(t)] = X(s).
Prof. Dr. Alberto Luiz Serpa - 2009 25](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-25-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
´E poss´ıvel escrever que
Y (s) =
γ
τs + 1
X(s),
com a seguinte fun¸c˜ao de transferˆencia:
G(s) =
γ
τs + 1
.
Considere os casos das entradas apresentadas a seguir.
1. Seja x(t) = u(t) uma entrada do tipo de degrau unit´ario. Logo tem-se
que
X(s) = L[u(t)] =
1
s
e a transformada de Laplace da equa¸c˜ao do sistema de primeira ordem
torna-se
Y (s) =
γ
τs + 1
1
s
.
Deseja-se determinar a resposta temporal y(t) atrav´es da expans˜ao em
fra¸c˜oes parciais, ou seja,
Y (s) =
γ
τ
s + 1
τ
1
s
=
c1
s + 1
τ
+
c2
s
. (4)
Multiplicando (4) por s + 1
τ
tem-se
γ
τs
= c1 + (s +
1
τ
)
c2
s
,
e fazendo s = −1
τ
, pois a equa¸c˜ao deve ser v´alida para qualquer s,
tem-se
γ
τ(−1
τ
)
= c1 + 0 ⇒ c1 = −γ.
Multiplicando (4) por s e calculando-se para s = 0 tem-se,
γ
τ
s + 1
τ
=
c1
s + 1
τ
s + c2 ⇒ c2 = γ.
Logo,
Y (s) =
γ
s
−
γ
s + 1
τ
.
Fazendo a anti-transformada de Laplace tem-se:
L−1
γ
1
s
−
1
s + 1
τ
= γ(1 − e− 1
τ
t
) = y(t), t ≥ 0.
Prof. Dr. Alberto Luiz Serpa - 2009 26](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-26-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
2. Seja x(t) = δ(t) um impulso unit´ario. A transformada de Laplace do
impulso unit´ario ´e
X(s) = L[δ(t)] = 1.
e a transformada de Laplace da equa¸c˜ao do sistema de primeira ordem
torna-se
Y (s) = G(s) =
γ
τ
s + 1
τ
.
A resposta ao impulso pode ser encontrada atrav´es da transformada
inversa, ou seja,
y(t) = L−1
γ
τ
s + 1
τ
=
γ
τ
e− t
τ , t ≥ 0,
cuja representa¸c˜ao gr´afica est´a na Figura 15.
t
y(t)γ
τ
Figura 15: Resposta ao impulso de um sistema de primeira ordem.
3. Seja x(t) = tu(t) uma rampa unit´aria. A transformada de Laplace da
rampa unit´aria ´e
X(s) = L[tu(t)] =
1
s2
,
e a transformada da equa¸c˜ao da resposta do sistema de primeira ordem
torna-se
Y (s) =
γ
τ
s + 1
τ
1
s2
=
c1
s2
+
c2
s
+
c3
s + 1
τ
. (5)
As constantes da expans˜ao em fra¸c˜oes parciais podem ent˜ao ser calcu-
ladas. Multiplicando (5) por s + 1
τ
e fazendo s = −1
τ
tem-se
c3 =
γ
τ
s2
s=− 1
τ
=
γ
τ
−
τ
1
2
= γτ.
Prof. Dr. Alberto Luiz Serpa - 2009 27](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-27-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
Multiplicando (5) por s2
tem-se
γ
τ
s + 1
τ
= c1 + sc2 + s2 c3
s + 1
τ
, (6)
e fazendo s = 0, tem-se
c1 =
γ
τ
s + 1
τ s=0
= γ.
Derivando (6) com rela¸c˜ao a s obt´em-se
−γ
τ
(s + 1
τ
)2
= c2 +
d
ds
s2 c3
s + 1
τ
,
e fazendo s = 0 obt´em-se
c2 =
−γ
τ
(1
τ
)2
= −γτ.
Logo, a transformada de Laplace na forma de fra¸c˜oes parciais ´e
Y (s) =
γτ
s + 1
τ
+
γ
s2
−
γτ
s
,
cuja anti-transformada ser´a dada por
y(t) = L−1
[Y (s)] ⇒ y(t) = γ τe− t
τ + t − τ , t ≥ 0.
A resposta temporal ´e ilustrada na Figura 16.
τ t
y(t)
γ
resposta
entrada
Figura 16: Resposta `a rampa unit´aria de sistema de primeira ordem.
Prof. Dr. Alberto Luiz Serpa - 2009 28](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-28-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
4. Seja uma entrada senoidal na forma x(t) = senwt. A transformada de
Laplace de x(t) ´e
X(s) = L[senwt] =
w
s2 + w2
,
e a transformada da equa¸c˜ao da resposta do sistema de primeira ordem
torna-se
Y (s) =
γ
τ
s + 1
τ
w
s2 + w2
.
Como s2
+ w2
= (s + jw)(s − jw) ´e poss´ıvel escrever que
γ
τ
s + 1
τ
w
s2 + w2
=
c1
s + 1
τ
+
c2
s + jw
+
c3
s − jw
. (7)
As constantes das fra¸c˜oes parciais podem ser calculadas, ou seja,
c1 =
γ
τ
w
s2 + w2
s=− 1
τ
=
γ
τ
w
(−1
τ
)2 + w2
=
γwτ
1 + w2τ2
,
c2 =
γ
τ
s + 1
τ
w
s − jw s=−jw
=
γ w
τ
(−jw + 1
τ
)(−2jw)
,
c3 =
γ w
τ
(s + 1
τ
)(s + jw) s=jw
=
γ w
τ
(jw + 1
τ
)(2jw)
.
A transformada de Laplace na forma de fra¸c˜oes parciais torna-se:
Y (s) = γ wτ
1+w2τ2
1
s+ 1
τ
+
+
w
τ
(−jw+ 1
τ
)(−2jw)
1
s+jw
+
w
τ
(jw+ 1
τ
)(2jw)
1
(s−jw)
.
A anti-transformada de Laplace pode ser agora determinada,
y(t) = L−1
[Y (s)].
Para cada um dos termos tem-se:
L−1
γ
wτ
1 + w2τ2
1
s + 1
τ
= γ
wτ
1 + w2τ2
e− t
τ ,
L−1
γ
w
τ
(−jw + 1
τ
)(−2jw)
1
s + jw
= γ
w
τ
(−jw + 1
τ
)(−2jw)
e−jwt
,
Prof. Dr. Alberto Luiz Serpa - 2009 29](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-29-320.jpg)



















![Controle de Sistemas em Tempo Cont´ınuo
8.1 Resposta ao impulso e convolu¸c˜ao
Seja um sistema representado por
Y (s) = G(s)X(s),
onde G(s) ´e a fun¸c˜ao de transferˆencia.
Sabe-se que a multiplica¸c˜ao no dom´ınio de Laplace ´e equivalente `a con-
volu¸c˜ao no dom´ınio do tempo. Portanto,
y(t) =
t
0
x(τ)g(t − τ)dτ =
t
0
g(τ)x(t − τ)dτ,
com g(t) = 0 e x(t) = 0 para t < 0.
Seja uma entrada do tipo impulso unit´ario, x(t) = δ(t), com condi¸c˜oes
iniciais nulas. Logo, X(s) = L[δ(t)] = 1, e ent˜ao
Y (s) = G(s).
Logo,
y(t) = L−1
[G(s)] = g(t),
´e a resposta ao impulso, ou seja, a transformada de Laplace da resposta ao
impulso de um sistema fornece a respectiva fun¸c˜ao de transferˆencia.
Na pr´atica, ´e poss´ıvel aproximar uma fun¸c˜ao impulso por uma fun¸c˜ao
pulso de amplitude grande e de dura¸c˜ao pequena cuja ´area seja unit´aria
conforme mostrado na Figura 10. Nota-se que quando t0 → 0 o pulso tende ao
impulso. Portanto, a resposta de um sistema a um pulso de grande amplitude
e de pequena dura¸c˜ao (´area unit´aria) tende `a resposta do impulso do sistema.
8.2 Matriz de transferˆencia
O conceito de matriz de transferˆencia ´e aplic´avel ao caso de sistemas com
m´ultiplas entradas e m´ultiplas sa´ıdas.
Considere um sistema com m entradas e n sa´ıdas. As m entradas carac-
terizam o vetor de entrada. As n sa´ıdas caracterizam o vetor de sa´ıda.
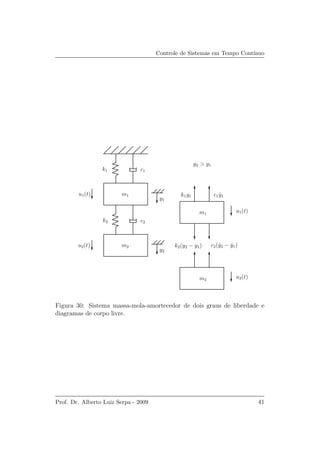
Seja, por exemplo, um sistema com duas entradas e duas sa´ıdas conforme
esquematizado na Figura 40.
A rela¸c˜ao entre as sa´ıdas e as entradas ´e dada por
Y1(s) = G11(s)X1(s) + G12(s)X2(s),
Y2(s) = G21(s)X1(s) + G22(s)X2(s).
Prof. Dr. Alberto Luiz Serpa - 2009 52](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-52-320.jpg)










![Controle de Sistemas em Tempo Cont´ınuo
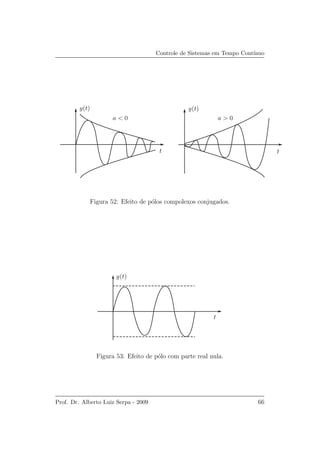
Da an´alise anterior, ´e poss´ıvel concluir que:
• P´olos com parte real negativa, isto ´e, localizados no semi-plano es-
querdo do plano complexo, contribuem com resposta est´avel.
• P´olos com parte real positiva, isto ´e, localizados no semi-plano direito
do plano complexo, contribuem com resposta crescente com o tempo
ou inst´avel.
• P´olos simples com parte real nula, isto ´e, sobre o eixo imagin´ario, con-
tribuem com resposta constante ou senoidal.
• P´olos m´ultiplos na origem ou sobre o eixo imagin´ario acarretam insta-
bilidade.
Uma avalia¸c˜ao da estabilidade natural pode ser feita tamb´em atrav´es da
resposta ao impulso. Lembrando que Y (s) = G(s)F(s) e que se F(s) = 1,
ou seja, f(t) = δ(t) um impulso unit´ario, ent˜ao,
L−1
[Y (s)] = L−1
[G(s)] = y(t),
onde y(t) ´e a resposta ao impulso do sistema, e que permite verificar a ins-
tabilidade se esta crescer de forma ilimitada.
Exemplo: Discutir a estabilidade do sistema G1(s) = 1
s
.
Este sistema possui um p´olo simples na origem, caracterizando uma res-
posta natural marginalmente est´avel. A resposta ao impulso deste sistema ´e
um degrau u(t), que ´e limitada.
Exemplo: Discutir a estabilidade do sistema G2(s) = 1000
s2+100
.
Este sistema possui p´olos complexos conjugados sobre o eixo imagin´ario,
caracterizando uma resposta senoidal marginalmente est´avel. A resposta ao
impulso deste sistema ´e 100sen(10t)u(t), que ´e limitada.
Exemplo: Discutir a estabilidade do sistema G3(s) = 1
s2 .
Este sistema possui p´olos m´ultiplos na origem, e ´e portanto inst´avel. A
resposta ao impulso deste sistema ´e tu(t), que cresce de forma ilimitada.
10.2 Estabilidade BIBO
O conceito de estabilidade BIBO (bounded input - bounded output) estabe-
lece que o sistema ´e est´avel se a resposta permanece limitada para qualquer
entrada limitada.
Prof. Dr. Alberto Luiz Serpa - 2009 67](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-67-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
A rela¸c˜ao entre a resposta Y (s) e a entrada F(s) de um sistema pode ser
escrita como
Y (s) = G(s)F(s),
e usando a propriedade de convolu¸c˜ao pode-se escrever que
y(t) = L−1
[G(s)F(s)] = g(t) ∗ f(t) =
t
0
g(τ)f(t − τ)dτ.
Se a entrada ´e limitada, ent˜ao pode-se escrever que
|f(t)| ≤ M < ∞.
Para que a resposta seja limitada deseja-se que
|y(t)| =
t
0
g(τ)f(t − τ)dτ ≤
t
0
|g(τ)||f(t − τ)|dτ,
e conseq¨uentemente ´e poss´ıvel escrever que
|y(t)| ≤ M
t
0
|g(τ)|dτ.
Para que a resposta |y(t)| seja limitada, deve-se ter que
t
0
|g(τ)|dτ < ∞,
que significa que a resposta ao impulso do sistema deve ser limitada.
11 Resposta em frequˆencia
11.1 Rela¸c˜ao de amplitude e ˆangulo de fase
A resposta em regime de um sistema linear invariante no tempo a uma en-
trada senoidal ´e tamb´em de forma senoidal, com amplitude e fase distin-
tos da entrada e dependentes das caracter´ısticas dinˆamicas do sistema e da
frequˆencia de entrada.
Seja um sistema descrito por
Y (s)
F(s)
= G(s) =
Q(s)
P(s)
,
com Q(s) e P(s) polinˆomios s.
Prof. Dr. Alberto Luiz Serpa - 2009 68](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-68-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
Seja uma entrada f(t) senoidal. Logo,
f(t) = Asenwt ⇒ F(s) = L[f(t)] =
Aw
s2 + w2
,
e consequentemente,
Y (s) = G(s)
Aw
s2 + w2
.
Uma expans˜ao em fra¸c˜oes parciais pode ser escrita como
Y (s) =
C1
(s − p1)
+
C2
(s − p2)
+ . . . +
Cn
s − pn
termos transit´orios
+
K1
s + jw
+
K2
s − jw
termos de regime
.
Realizando a anti-transformada de Laplace tem-se
y(t) =
n
i=1
Ciepit
+ K1e−jwt
+ K2ejwt
onde a somat´oria pode ser desconsiderada pois representa os termos tran-
sit´orios. Pressup˜oe-se que G(s) ´e est´avel.
Logo, a resposta de regime ´e
y(t) = K1e−jwt
+ K2ejwt
.
As constantes correspondentes s˜ao:
K1 = (s + jw)G(s)
Aw
(s + jw)(s − jw) s=−jw
= G(−jw)
Aw
−2jw
= G(−jw)
A
−2j
,
K2 = (s − jw)G(s)
Aw
(s + jw)(s − jw) s=jw
= G(jw)
A
2j
,
Pode-se escrever
G(jw) = |G(jw)|ejφ
, G(−jw) = |G(jw)|e−jφ
,
e
φ = G(jw) = tan−1 Im(G(jw))
Re(G(jw))
.
Consequentemente,
y(t) = −A
2j
|G(jw)|e−jφ
e−jwt
+ A
2j
|G(jw)|ejφ
ejwt
=
= A|G(jw)| ej(wt+φ)−e−j(wt+φ)
2j
=
= A|G(jw)|sen(wt + φ).
Prof. Dr. Alberto Luiz Serpa - 2009 69](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-69-320.jpg)

![Controle de Sistemas em Tempo Cont´ınuo
|G(jw)| =
|γ|w2
n
[(w2
n − w2)2 + 4ξ2w2
nw2]
1
2
= RA,
φ = −tan−1 2ξwnw
(w2
n − w2)
.
11.4 Resposta em freq¨uˆencia de um integrador puro
Seja
G(s) =
γ
s
,
ent˜ao,
G(jw) =
γ
jw
= −j
γ
w
=
γ
w
e−jφ
,
e se verifica que
|G(jw)| =
γ
w
= RA, φ = tan−1
−γ
w
0
= −
π
2
.
11.5 Diagramas de Bode
Existem dois gr´aficos usuais para representar as caracter´ısticas de resposta
em freq¨uˆencia de sistemas.
• Diagrama de amplitudes: plota as RA (em decib´eis, dB) em fun¸c˜ao de
w (escala log).
• Digrama de fases: plota as fases φ em fun¸c˜ao de w em escala log.
Para isso define-se a rela¸c˜ao de amplitudes em dB como
RAdB = 20 log RA.
S˜ao apresentados a seguir os diagramas de Bode de alguns sistemas t´ıpicos.
11.5.1 Diagramas de Bode para o integrador puro
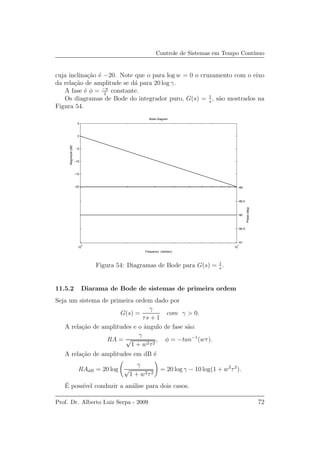
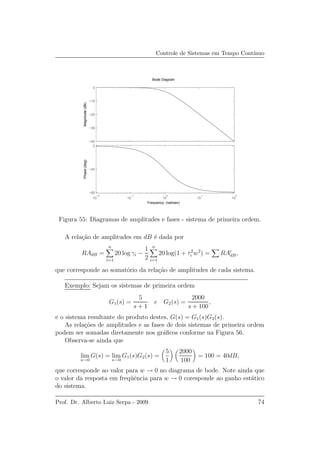
A rela¸c˜ao de amplitudes para o integrador puro permite escrever que
RAdB = 20 log
γ
w
= 20 log γ − 20 log w,
que ´e uma reta na escala dB-log do tipo
y = C − 20x,
Prof. Dr. Alberto Luiz Serpa - 2009 71](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-71-320.jpg)

![Controle de Sistemas em Tempo Cont´ınuo
−100
−50
0
50
Magnitude(dB)
10
−2
10
−1
10
0
10
1
10
2
10
3
10
4
−180
−135
−90
−45
0
Phase(deg)
Bode Diagram
Frequency (rad/sec)
G1(s)
G2(s)
G(s)
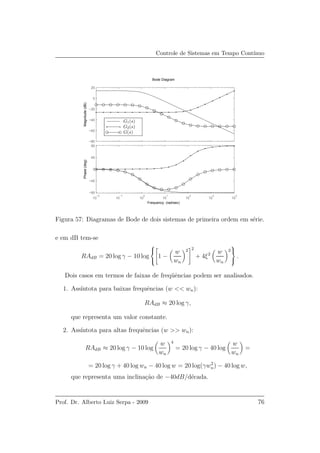
Figura 56: Diagramas de Bode de dois sistemas de primeira ordem em s´erie.
Observa-se cada p´olo simples contribui com uma queda de -20dB/d´ecada
no diagrama de Bode. Note que um zero ir´a alterar o sinal da inclina¸c˜ao
da reta, contribuindo com um efeito de +20dB/d´ecada, assim como uma
contrinui¸c˜ao positiva na fase, como ilustrado no exemplo a seguir.
Exemplo: Sejam os sistemas de primeira ordem
G1(s) =
5
s + 1
e G2(s) =
s + 100
2000
,
e o sistema resultante do produto destes, G(s) = G1(s)G2(s).
As rela¸c˜oes de amplitudes e as fases de dois sistemas de primeira ordem
podem ser somadas diretamente nos gr´aficos conforme na Figura 57.
11.5.4 Diagrama de Bode de sistemas de segunda ordem
A rela¸c˜ao de amplitudes para um sistema de segunda ordem ´e
RA =
γ
[1 − ( w
wn
)2]2 + 4ξ2( w
wn
)2
,
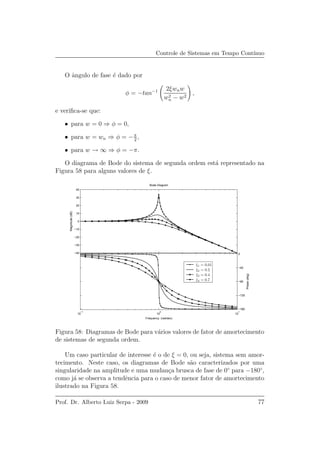
Prof. Dr. Alberto Luiz Serpa - 2009 75](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-75-320.jpg)






![Controle de Sistemas em Tempo Cont´ınuo
u(t) h(t)
atuador processo sensor
Figura 66: Rela¸c˜ao entre deslocamento da v´alvula e n´ıvel do tanque.
h(t) Is(t)p(t) r(t)
prim´ario transdutor condicionador
Figura 67: Estrutura do sensor - rela¸c˜ao entre altura e corrente.
el´etrica r(t), que por sua vez determina uma corrente de sa´ıda do sensor
Is(t).
A rela¸c˜ao entre altura e press˜ao ´e dada por
p(t) = ρgh(t) =
1000 × 9.81
105
h(t) [bar],
onde se considerou que o l´ıquido ´e ´agua.
Tendo em mente que a altura m´axima do tanque ´e de 4m, verifica-se que
a press˜ao m´axima a ser medida ´e de 0.3924 bar, valor este que permite a
escolha de um sensor adequado.
Os elementos de transdu¸c˜ao e de condicionamento geralmente tˆem uma
faixa de opera¸c˜ao at´e 20mA. Neste caso, calcula-se o respectivo ganho asso-
ciado, ou seja,
0.3924 bar ←→ 20mA ⇒
20mA
0.3924 bar
= 50.968,
de forma que se escreve a rela¸c˜ao
Is(t) = 50.968p(t) = 50.968
9810
105
h(t) ⇒ Is(t) ∼= 5h(t).
A estrutura do atuador pode ser esquematizada conforme na Figura 68.
Uma v´alvula eletro-pneum´atica ´e adequada neste caso e transforma cor-
rente em press˜ao. Para uma faixa de opera¸c˜ao de 0 at´e 20mA tem-se a sa´ıda
de 0 at´e 6 bar, caracterizando um ganho dado por
6 bar
20mA
= 0.3 bar/mA,
ou seja,
p(t) = 0.3Ie(t).
Prof. Dr. Alberto Luiz Serpa - 2009 87](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-87-320.jpg)



![Controle de Sistemas em Tempo Cont´ınuo
e substituindo a equa¸c˜ao do n´ıvel do primeiro tanque tem-se
H2 =
γ2
τ2s + 1
1
R1
γ1
τ1s + 1
Qe1.
Como R1 = γ1, escreve-se para o sistema de tanques independentes:
H2 =
γ2
(τ2s + 1)(τ1s + 1)
Qe1 =
γ2
τ1τ2s2 + (τ1 + τ2)s + 1
Qe1,
ou ainda,
[τ1τ2s2
+ (τ1 + τ2)s + 1]H2 = γ2Qe1 ⇒ τ1τ2
¨h2 + (τ1 + τ2)˙h2 + h2 = γ2qe1,
que corresponde a uma equa¸c˜ao diferencial de um sistema de segunda ordem.
Este sistema pode ser representado em termos de diagrama de blocos
como na Figura 72.
qe1 h1 h2γ1
τ1
γ2
τ2
1
γ1
1
τ1
1
τ2
−−
Figura 72: Diagrama de blocos do sistema de tanques independentes.
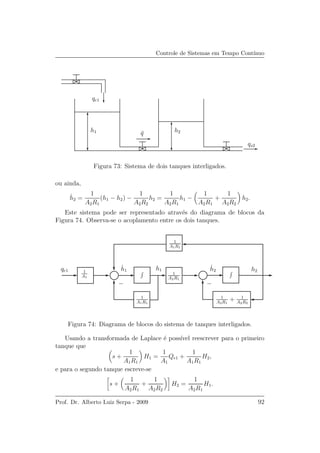
12.4 Sistema de dois tanques interligados
Seja um sistema composto por dois tanques interligados como mostrado na
Figura 73.
Para o primeiro tanque pode-se escrever:
A1
˙h1 = qe1 − ¯q, ¯q =
1
R1
(h1 − h2),
ou ainda,
˙h1 =
1
A1
qe1 −
1
A1R1
(h1 − h2) =
1
A1
qe1 −
1
A1R1
h1 +
1
A1R1
h2.
Para o segundo tanque tem-se que
A2
˙h2 = ¯q − qs2, qs2 =
1
R2
h2,
Prof. Dr. Alberto Luiz Serpa - 2009 91](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-91-320.jpg)














![Controle de Sistemas em Tempo Cont´ınuo
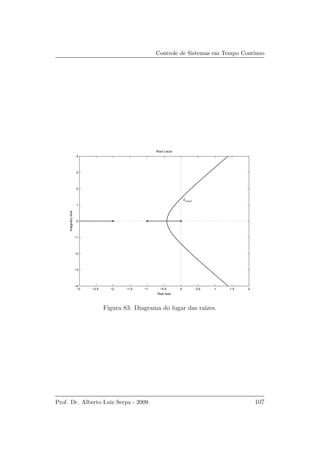
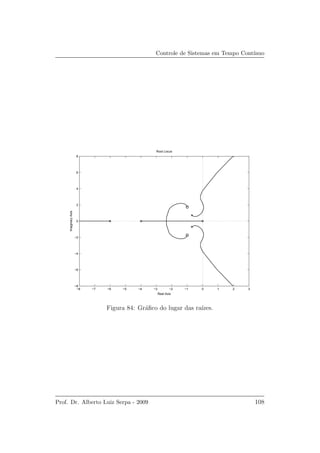
e est´a mostrado na Figura 84.
Verifica-se que os zeros da malha aberta s˜ao (−1+1.7321j, −1−1.7321j)
e os p´olos da malha aberta s˜ao (−0.7 ± 0.7141j, 0, −4, −6). Percorrendo o
gr´afico verifica-se que kmax = 17.5 ´e o limite para a estabilidade.
Exemplo: Seja o esquema da Figura 82, em que G(s) = 1
s(s+1)(s+2)
e
existe um ganho de valor 2 no ramo de realimenta¸c˜ao, ou seja, H(s) = 2.
Determinar o valor cr´ıtico do ganho proporcional k que multiplica a planta
de forma que o sistema de malha fechada esteja no limiar da estabilidade.
A equa¸c˜ao da malha fechada neste caso ´e
T(s) =
kP(s)
1 + kP(s)H(s)
,
e o gr´afico do lugar das ra´ızes pode ser determinado com o aux´ılio do MA-
TLAB com os seguintes comandos:
s=tf(’s’);
ps=1/(s*(s+1)*(s+2))
hs=2;
rlocus(ps*hs)
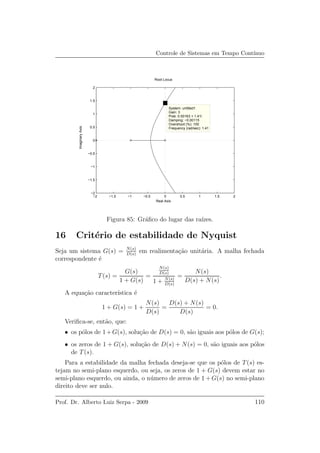
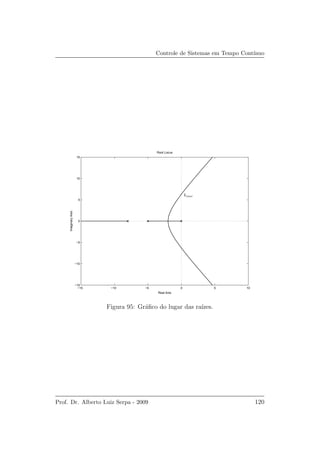
e est´a mostrado na Figura 85. Do gr´afico do lugar da ra´ızes verifica-se que o
ponto sobre o eixo imagin´ario, limiar da estabilidade, corresponde ao ganho
de k ≈ 3.
Para k = 3 a malha fechada ´e
T(s) =
3
s3 + 3s2 + 2s + 6
,
cujos p´olos s˜ao (−3.0, −0.0 ± 1.4142j), que permitem confimar o limiar da
estabilidade (existem p´olos sobre o eixo imagin´ario). O c´odigo MATLAB,
adicionado ao c´odigo anterior e que permite a verifica¸c˜ao, ´e:
k=3
ts=feedback(k*ps,hs) %fechar a malha com realimenta¸c~ao hs
[pts,gts]=pzmap(ts) %determinar os polos e zeros
Prof. Dr. Alberto Luiz Serpa - 2009 109](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-109-320.jpg)



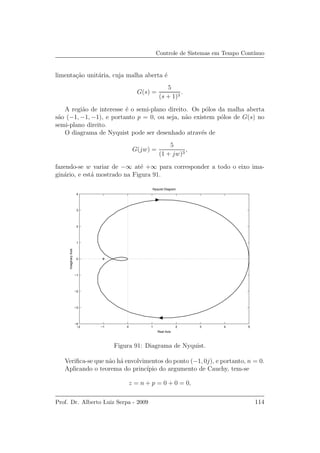
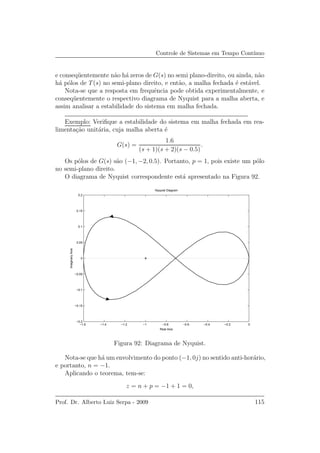
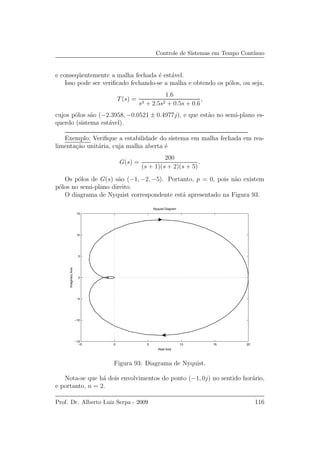


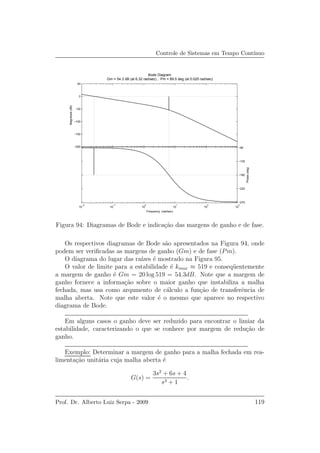










![Controle de Sistemas em Tempo Cont´ınuo
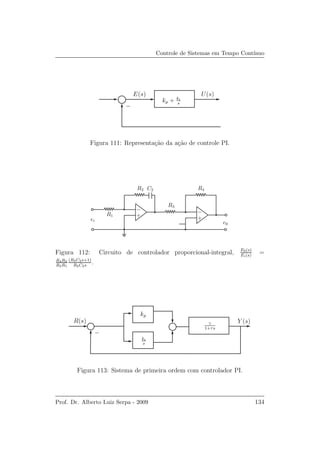
O diagrama de blocos ´e mostrado na Figura 113.
A fun¸c˜ao de transferˆencia de malha fechada, com realimenta¸c˜ao unit´aria,
´e dada por
Y (s)
R(s)
=
(kp + ki
s
)( γ
1+τs
)
1 + (kp + ki
s
)( γ
1+τs
)
=
γkps + γki
τs2 + (1 + γkp)s + γki
.
Para uma entrada degrau unit´ario tem-se que R(s) = 1
s
. Logo,
Y (s) =
γkps + γki
s [τs2 + (1 + γkp)s + γki]
.
´E poss´ıvel verificar que a malha fechada pode apresentar respostas com
caracter´ısticas distintas em fun¸c˜ao das ra´ızes do denominador (trata-se de
um sistema de segunda ordem).
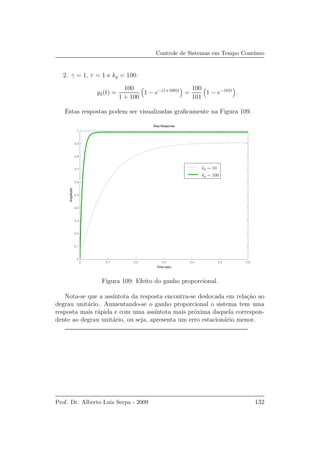
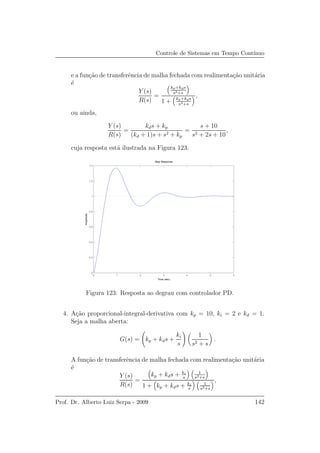
Para γ = 1, τ = 1, kp = 5 e ki = 2 tem-se
Y (s) =
5s + 2
s(s2 + 6s + 2)
,
cuja resposta ao degrau est´a ilustrada na Figura 114.
0 1 2 3 4 5 6 7 8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Step Response
Time (sec)
Amplitude
Figura 114: Sistema de primeira ordem com controlador PI - resposta ao
degrau.
Nota-se que o erro estacion´ario tende a zero.
Prof. Dr. Alberto Luiz Serpa - 2009 135](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-135-320.jpg)














![Controle de Sistemas em Tempo Cont´ınuo
0 0.5 1 1.5 2 2.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Step Response
Time (sec)
Amplitude
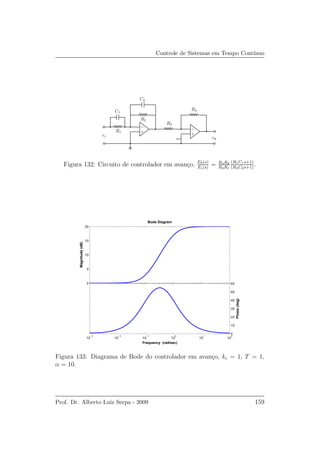
Figura 129: Resposta ao degrau da malha fechada.
tetap=angle(psD)
tetak=-pi-tetap
ampk=1/ampp
sigmaD=real(sD);
wD=imag(sD);
a=sigmaD^2-wD^2
b=sigmaD
alpha=sigmaD*ampk*cos(tetak)-wD*ampk*sin(tetak)
c=2*sigmaD*wD
d=wD
beta=wD*ampk*cos(tetak)+sigmaD*ampk*sin(tetak)
kp=(alpha*c-a*beta)/(b*c-a*d) %apenas PD
kd=(beta-d*kp)/c
ks=kp+kd*s
gs=ks*ps %malha aberta
ts=feedback(gs,1)
step(ts)
figure
margin(gs)
[p,z]=pzmap(ts)
Prof. Dr. Alberto Luiz Serpa - 2009 156](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-156-320.jpg)









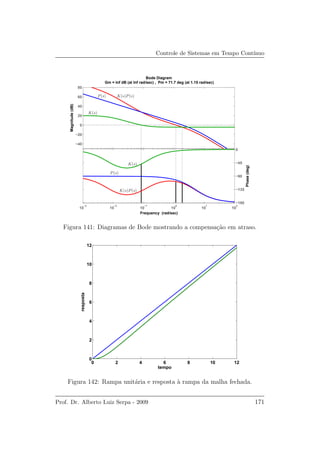
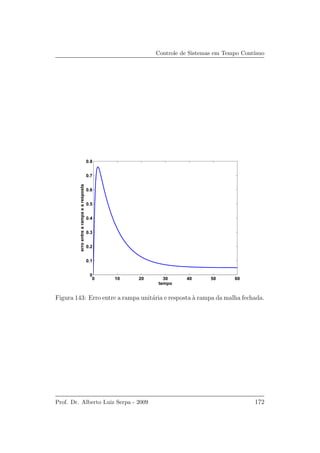




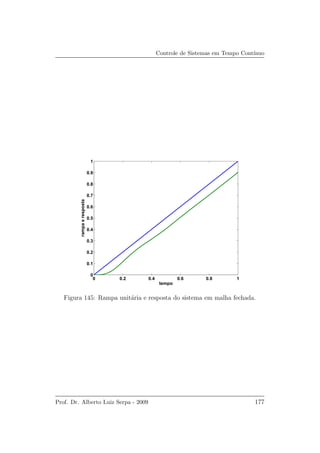



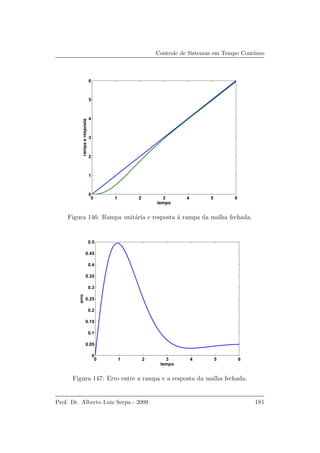
![Controle de Sistemas em Tempo Cont´ınuo
Um c´odigo MATLAB para o projeto avan¸co-atraso anal´ıtico com base no
lugar das ra´ızes ´e apresentado a seguir:
% Projeto avanco-atraso anal´ıtico (lugar ra´ızes)
% Erro estacion´ario `a rampa de 0.05,
% fator de amortecimento de 0.707,
% freq. natural de 1.5 rad/s,
% planta ps=10/(s(s+5)).
%
clear all; close all; clc;
s=tf(’s’);
ps=10/(s*(s+5));
kc=10 %calculado atraves do erro estacionario
qsi=0.707;
wn=1.5;
sD=-qsi*wn+j*wn*sqrt(1-qsi^2)
sigmaD=real(sD)
wD=imag(sD)
psD=freqresp(ps,sD)
ampp=abs(psD)
tetap=angle(psD)
ampk=1/ampp
tetak=-pi-tetap
T=-(sigmaD*ampk*sin(tetak)+kc*wD-wD*ampk*cos(tetak))/...
(ampk*sin(tetak)*(sigmaD^2+wD^2))
alpha=ampk*(kc*wD*cos(tetak)-wD*ampk+kc*sigmaD*sin(tetak))/...
(kc*(sigmaD*ampk*sin(tetak)+kc*wD-wD*ampk*cos(tetak)))
ks=kc*(alpha*T*s+1)/(T*s+1)
gs=ks*ps %malha aberta
margin(gs)
ts=feedback(gs,1) %malha fechada
[p,z]=pzmap(ts)
tss=ts/s; %rampa
step(ts)
t=0:0.01:6;
figure, y=step(tss,t);
figure, plot(t,t,t,y)
Prof. Dr. Alberto Luiz Serpa - 2009 182](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-182-320.jpg)



![Controle de Sistemas em Tempo Cont´ınuo
As vari´aveis de estado podem ser definidas como
y = x1,
dy
dt
= x2,
d2
y
dt2
= x3, . . . ,
dn−1
y
dtn−1
= xn.
Logo,
dx1
dt
= x2,
dx2
dt
= x3,
dx3
dt
= x4, . . . ,
dxn−1
dt
= xn,
e a equa¸c˜ao diferencial pode ser reescrita como
dxn
dt
= u(t) − a0x1 − a1x2 − a2x3 − . . . − an−1xn,
ou matricialmente
˙x = Ax + Bu,
onde
x =
x1
x2
...
xn
, A =
0 1 0 . . . 0
0 0 1 . . . 0
...
...
...
...
0 0 0 . . . 1
−a0 −a1 −a2 . . . −an−1
, B =
0
0
...
0
1
.
A sa´ıda ´e dada por
y = [1 0 . . . 0]
x1
x2
...
xn
ou
y = Cx,
com C = [1 0 . . . 0], quando se considerou como resposta apenas a vari´avel
y(t).
A fun¸c˜ao de transferˆencia neste caso ´e
Y (s)
U(s)
=
1
sn + an−1sn−1 + . . . + a1s + a0
,
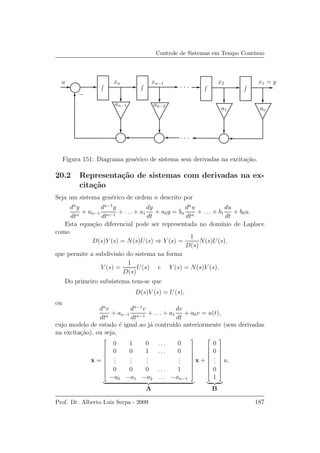
e um diagrama de blocos gen´erico ´e mostrado na Figura 151.
Esta forma de representa¸c˜ao de estado ´e conhecida como modelo canˆonico
de fase, devido ao vetor de estado ser formado por vari´aveis que s˜ao derivadas
sucessivas da anterior, portanto com uma diferen¸ca de fase de 90◦
entre elas.
Prof. Dr. Alberto Luiz Serpa - 2009 186](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-186-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
v = [1 0 0 . . . 0]
x1
x2
...
xn
,
com x1 = v, x2 = ˙v, x3 = ¨v, . . ., xn = dn−1v
dtn−1 .
Do segundo subsistema tem-se que
Y (s) = N(s)V (s),
ou ainda
y(t) = bn
dn
v
dtn
+ bn−1
dn−1
v
dtn−1
. . . + b1
dv
dt
+ b0v(t).
Substituindo os estados nesta equa¸c˜ao tem-se que
y(t) = bn ˙xn + bn−1xn + . . . + b1x2 + b0x1 =
= bn(−a0 − a1x2 − . . . − an−1xn + u) + bn−1xn + . . . + b1x2 + b0x1 =
(bn−1 − bnan−1)xn + . . . + (b1 − bna1)x2 + (b0 − bna0)x1 + bnu,
e matricialmente,
y =
b0 − bna0
b1 − bna1
...
bn−2 − bnan−2
bn−1 − bnan−1
t
C
x + bn
D
u.
Exemplo: Seja o sistema de ordem 3 descrito por
d3
y
dt3
+ a2 ¨y + a1 ˙y + a0y = b3
d3
u
dt3
+ b2 ¨u + b1 ˙u + b0u.
Aplicando a f´ormula deduzida anteriormente, escreve-se que
˙x1
˙x2
˙x3
=
0 1 0
0 0 1
−a0 −a1 −a2
x1
x2
x3
+
0
0
1
u,
y =
b0 − b3a0
b1 − b3a1
b2 − b3a2
t
x1
x2
x3
+ b3u.
Prof. Dr. Alberto Luiz Serpa - 2009 188](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-188-320.jpg)

![Controle de Sistemas em Tempo Cont´ınuo
que pode ser integrada sucessivamante permitindo obter
dn−1
xn
dtn−1
=
dn−1
y
dtn−1
− bn
dn−1
u
dtn−1
,
¨xn = ¨y − bn ¨u,
˙xn = ˙y − bn ˙u,
x(t) = y(t) − bnu(t) ⇒ y(t) = x(t) + bnu(t).
De
˙x1 = −a0y + b0u e y = xn + bnu,
tem-se que
˙x1 = −a0(xn + bnu) + b0u = −a0xn + (b0 − bna0)u.
De
¨x2 = −a1 ˙y + b1 ˙u + ˙x1 ⇒ ˙x2 = −a1y + b1u + x1,
e usando novamente y = xn + bnu tem-se que
˙x2 = −a1xn + (b1 − bna1)u + x1.
Generalizando ´e poss´ıvel escrever que
˙xn = −an−1xn + (bn−1 − bnan−1)u + xn−1,
que permite escrever a forma canˆonica observ´avel como
˙x1
˙x2
...
˙xn
=
0 0 . . . 0 −a0
1 0 0 −a1
...
...
...
...
0 0 1 −an−1
x1
x2
...
xn
+
b0 − bna0
b1 − bna1
...
bn−1 − bnan−1
u,
y = [0 0 . . . 0 1]
x1
x2
...
xn
+ bnu.
Nota-se que a matriz de estado n × n da forma observ´avel ´e a transposta
da matriz de estado da forma control´avel.
Exemplo: Para o sistema massa-mola-amortecedor regido por
¨y +
c
m
˙y +
k
m
y(t) =
1
m
u(t),
o modelo de estados na forma observ´avel ´e dado pelas matrizes:
A =
0 − k
m
1 − c
m
; B =
1
m
0
; C = [0 1] ; D = 0.
Prof. Dr. Alberto Luiz Serpa - 2009 190](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-190-320.jpg)



![Controle de Sistemas em Tempo Cont´ınuo
• Para o caso escalar tem-se:
˙x = ax
L
→ sx(s) − x(0) = ax(s),
x(s) =
x(0)
s − a
= (s − a)−1
x(0)
L−1
→ x(t) = eat
x(0).
• Para o caso matricial tem-se:
˙x = Ax
L
→ sx(s) − x(0) = Ax(s),
(sI − A)x(s) = x(0),
x(s) = (sI − A)−1
x(0)
L−1
→ x(t) = eAt
x(0).
20.7 Matriz de transi¸c˜ao de estados
A solu¸c˜ao da equa¸c˜ao homogˆenea ˙x = Ax pode ser escrita como
x(t) = φ(t)x(0), (14)
onde φ(t) ´e uma matriz n × n e ´e solu¸c˜ao de
˙φ(t) = Aφ(t), φ(0) = I.
Note que
x(0) = φ(0)x(0),
˙x(t) = ˙φ(t)x(0) = Aφ(t)x(0) = Ax(t).
A solu¸c˜ao de ˙φ(t) = Aφ(t) ´e
φ(t) = eAt
φ(0) = eAt
= L−1
[(sI − A)−1
].
´E poss´ıvel verificar que φ(t)−1
= e−At
= φ(−t).
Com base na equa¸c˜ao (14) nota-se que a matriz φ(t) representa uma
transforma¸c˜ao da condi¸c˜ao inicial. Esta matriz ´e conhecida como matriz de
transi¸c˜ao de estados e cont´em toda a informa¸c˜ao sobre o comportamento
natural do sistema.
Se os autovalores λ1, λ2, . . ., λn da matriz A forem distintos, φ(t) conter´a
n exponenciais eλ1t
, eλ2t
, . . ., eλnt
.
Se houver multiplicidade dos autovalores de A ent˜ao φ(t) conter´a al´em
dos termos do tipo eλt
, termos do tipo teλt
.
Prof. Dr. Alberto Luiz Serpa - 2009 194](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-194-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
Exemplo: Obter a matriz de transi¸c˜ao de estados e sua inversa para o
seguinte sistema
˙x1
˙x2
˙x
=
0 1
−2 −3
A
x1
x2
x
.
A matriz de transi¸c˜ao de estados ´e dada por
φ(t) = eAt
= L−1
[(sI − A)−1
].
Calculando
sI − A =
s 0
0 s
−
0 1
−2 −3
=
s −1
2 s + 3
,
(sI − A)−1
=
1
(s + 1)(s + 2)
s + 3 1
−2 s
=
s+3
(s+1)(s+2)
1
(s+1)(s+2)
−2
(s+1)(s+2)
s
(s+1)(s+2)
.
Logo,
φ(t) = L−1
(sI − A)−1
=
2e−t
− e−2t
e−t
− e−2t
−2e−t
+ 2e−2t
−e−t
+ 2e−2t = eAt
,
e a inversa pode ser calculada como
φ(t)−1
= φ(−t) =
2et
− e2t
et
− e2t
−2et
+ 2e2t
−et
+ 2e2t .
Um c´odigo MATLAB para o c´alculo da exponencial matricial para este
exemplo ´e:
clear all; close all; clc;
A=[0 1; -2 -3];
syms t
phi=expm(A*t)
20.8 Solu¸c˜ao das equa¸c˜oes de estado n˜ao homogˆeneas
• Seja o caso escalar:
˙x = ax + bu ⇒ ˙x − ax = bu,
Prof. Dr. Alberto Luiz Serpa - 2009 195](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-195-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
ent˜ao
e−at
( ˙x − ax) = e−at
bu,
ou ainda,
d
dt
(e−at
x(t)) = e−at
bu(t).
Integrando entre 0 e t obt´em-se
e−at
x(t) = x(0) +
t
0
e−aτ
bu(τ)dτ,
x(t) = eat
x(0) + eat
t
0
e−aτ
bu(τ)dτ,
que ´e a solu¸c˜ao da equa¸c˜ao diferencial de primeira ordem do caso esca-
lar.
• Seja o caso matricial
˙x = Ax + Bu.
Da mesma forma que foi feito no caso escalar tem-se que
x(t) = eAt
x(0) +
t
0
eA(t−τ)
Bu(τ)dτ,
x(t) = φ(t)x(0) +
t
0
φ(t − τ)Bu(τ)dτ,
que representa a solu¸c˜ao do sistema de equa¸c˜oes diferenciais de primeira
dado pela equa¸c˜ao de estado.
As equa¸c˜oes de estado podem ser resolvidas pelo enfoque da transformada
de Laplace, ou seja,
sX(s) − x(0) = AX(s) + BU(s),
(sI − A)X(s) = x(0) + BU(s),
X(s) = (sI − A)−1
x(0) + (sI − A)−1
BU(s),
X(s) = L[eAt
]x(0) + L[eAt
]BU(s),
ou aplicando a anti-transformada de Laplace,
x(t) = eAt
x(0) +
t
0
eA(t−τ)
Bu(τ)dτ,
onde se utilizou a propriedade de que o produto no dom´ınio s representa a
convolu¸c˜ao do dom´ınio t.
Prof. Dr. Alberto Luiz Serpa - 2009 196](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-196-320.jpg)


![Controle de Sistemas em Tempo Cont´ınuo
ou ainda
Heq(s) =
Kx(s)
Y (s)
=
Kx(s)
Cx(s)
.
Contudo,
x(s) = (sI − A)−1
BU(s).
Logo,
Heq(s) =
K(sI − A)−1
B
C(sI − A)−1B
,
que ´e uma fun¸c˜ao de transferˆencia de uma entrada e uma sa´ıda neste caso.
Observando que a planta a ser controlada ´e dada por P(s) = C(sI −
A)−1
B, verifica-se que a fun¸c˜ao de malha de malha aberta (“loop”) ´e dada
por
L(s) = P(s)Heq(s) = K(sI − A)−1
B,
o que permite os c´alculos das margens de estabilidade relativa atrav´es do
sistema determinado pelas matrizes de estado (A, B, K, 0).
Neste caso de regulador, o sinal de controle devido a uma perturba¸c˜ao
em termos de condi¸c˜oes iniciais pode ser determinado atrav´es do seguinte
sistema na forma de estados
˙x = Akx, u = −Kx,
ou seja, pelo modelo de estado determinado pelas matrizes (Ak, 0, −K, 0).
Uma outra forma de determinar o sinal de controle ´e calcular os estados, e
ent˜ao calcular diretamente u(t) = −Kx(t).
21.2 F´ormula de Ackermann
Seja o sistema
˙x = Ax + Bu,
e a realimenta¸c˜ao de estados u = −Kx. Consequentemente, a malha fechada
correspondente ´e
˙x = (A − BK)x = AKx,
onde AK = A − BK.
A equa¸c˜ao caracter´ıtica correspondente
det[sI − (A + BK)] = det[sI − AK] = (s − µ1)(s − µ2) . . . (s − µn) =
= sn
+ α1sn−1
+ . . . + αn−1s + αn = 0,
onde µ1, µ2, . . ., µn s˜ao os p´olos da malha fechada.
Prof. Dr. Alberto Luiz Serpa - 2009 199](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-199-320.jpg)

![Controle de Sistemas em Tempo Cont´ınuo
ou tamb´em
[0 0 1] B AB A2
B
−1
ψ(A) = [0 0 1]
α2K + α1KAK + KA2
K
α1K + KAK
K
,
que permite isolar K, i.e.,
K = [0 0 1] B AB A2
B
−1
ψ(A).
Pode-se escrever para n qualquer que
K = [0 0 . . . 0 1] B AB . . . An−1
B
−1
ψ(A)
que ´e conhecida como a f´ormula de Ackerman, que requer que a matriz de
controlabilidade seja invers´ıvel, ou seja,
det B AB . . . An−1
B = 0.
Exemplo: Um bloco de massa unit´aria deve permanecer na sua posi¸c˜ao
inicial. Ao ser perturbado com uma condi¸c˜ao inicial ele deve retornar `a esta
posi¸c˜ao de forma criticamente amortecida e com um tempo de estabiliza¸c˜ao
a 2% de 2s. Determine os ganhos de realimenta¸c˜ao de estados para esta
situa¸c˜ao e verifique a resposta em termos da posi¸c˜ao e da velocidade quando
o bloco ´e submetido `a uma condi¸c˜ao inicial y(0) = 0.1.
A equa¸c˜ao diferencial correspondente ´e
¨y = u(t).
Sejam os estados x1 = y e x2 = ˙y. Logo escreve-se que
˙x1
˙x2
=
0 1
0 0
x1
x2
+
0
1
u,
y = [1 0]
x1
x2
.
A matriz de controlabilidade neste caso ´e
M = [B AB] =
0 1
1 0
,
cujo determinante ´e
detM = −1,
Prof. Dr. Alberto Luiz Serpa - 2009 201](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-201-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
e conseq¨uentemente tem-se um sistema control´avel.
Os requisitos de projeto s˜ao ξ = 1 e Te2% = 2. Logo,
Te2% =
4
ξwn
⇒ wn =
4
ξTe2%
= 2rad/s.
Portanto, os p´olos desejados s˜ao
µ1,2 = −ξwn ± jwn 1 − ξ2 = −2 ± 0j.
Logo,
φ(s) = (s + 2)(s + 2) = s2
+ 4s + 4.
Aplicando a f´ormula de Ackermann obt´em-se os ganhos da realimenta¸c˜ao
de estados, ou seja,
K = [0 1]M−1
ψ(A) =
= [0 1]
0 1
1 0
−1
0 1
0 0
2
+ 4
0 1
0 0
+ 4
1 0
0 1
= [4 4].
A matriz de estado de malha fechada ´e
AK = A − BK =
0 1
0 0
−
0
1
[4 4] =
0 1
−4 −4
.
´E poss´ıvel verificar a posi¸c˜ao e a velocidade deste sistema quando sub-
metido `a uma condi¸c˜ao inicial. Note que o sistema em malha fechada ´e
homogˆeneo (regulador) e o papel do controlador ´e assegurar que o sistema
retorne ao seu estado de equil´ıbrio quando for submetido `a um perturba¸c˜ao
na forma de uma condi¸c˜ao inicial. A matriz de transi¸c˜ao de estados pode ser
utilizada neste caso para o c´alculo da resposta em fun¸c˜ao do tempo.
Um c´odigo MATLAB para este exemplo ´e apresentado a seguir, que gera
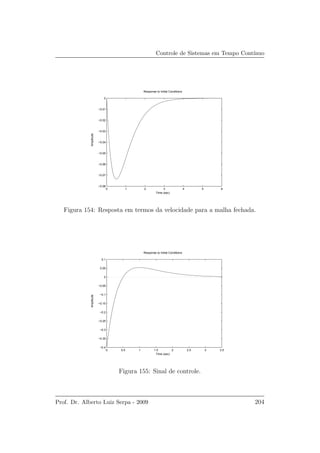
os gr´aficos da resposta da malha fechada para a posi¸c˜ao e para a veloci-
dade mostrados nas Figura 153 e 154 respectivamente. O sinal de controle ´e
mostrado na Figura 155.
%realimenta¸c~ao de estados - regulador
clear all; close all; clc;
A=[0 1; 0 0];
B=[0; 1];
C=[1 0];
D=0;
M=ctrb(A,B) %matriz de controlabilidade
detM=det(M)
Prof. Dr. Alberto Luiz Serpa - 2009 202](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-202-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
qsi=1; te2=2;
wn=4/(qsi*te2)
polosd=[-qsi*wn+wn*sqrt(1-qsi^2) -qsi*wn-wn*sqrt(1-qsi^2)] %polos desejados
K=acker(A,B,polosd)
Ak=A-B*K
Bk=[0; 0];
Ck=[1 0] %sa´ıda em posi¸c~ao
Dk=0
CI=[0.1 0] %condi¸c~oes iniciais
initial(Ak,Bk,Ck,Dk,CI) %resposta da posi¸c~ao `a condi¸c~ao inicial
[y,x,t]=initial(Ak,Bk,Ck,Dk,CI); %sa´ıda y e estados x, para o tempo t
Ck=[0 1] %sa´ıda em velocidade
figure, initial(Ak,Bk,Ck,Dk,CI) %resposta da velocidade `a condi¸c~ao inicial
figure, initial(Ak,Bk,-K,Dk,CI) %sinal de controle
%forma alternativa de calculo do sinal de controle
u=-K*x’;
figure, plot(t,u)
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
Response to Initial Conditions
Time (sec)
Amplitude
Figura 153: Resposta em termos de posi¸c˜ao para a malha fechada.
Prof. Dr. Alberto Luiz Serpa - 2009 203](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-203-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
21.3 Caso de rastreador - entrada degrau
Considere um problema de rastreamento com entrada do tipo degrau. Este
problema pode ser resolvido adequadamente pela realimenta¸c˜ao de estados,
compensando inclusive o erro estacion´ario no caso da resposta ao degrau.
Seja o sistema
˙x = Ax + Bu, y = Cx,
onde D = 0 sem perda de generalidade.
Seja a matriz de realimenta¸c˜ao K e por conveniˆencia um ganho kp no
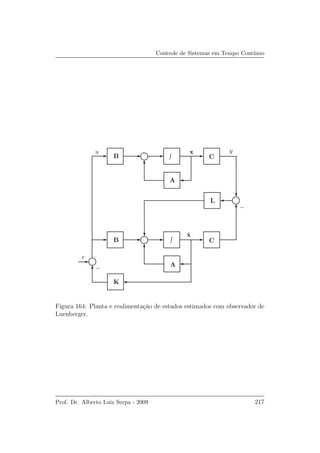
ramo de malha aberta conforme mostrado na Figura 156.
r(t) u(t) x(t) y(t)
kp ˙x = Ax + Bu C
K
−
Figura 156: Esquema de realimenta¸c˜ao de estados.
Observando o diagrama de blocos pode-se escrever que
u = kp(r − Kx).
Substituindo este resultado na equa¸c˜ao de estados tem-se
˙x = Ax + B[kp(r − Kx)],
˙x = (A − kpBK)x + kpBr(t).
Definindo as novas matrizes
Ak = A − kpBK,
Bk = kpB,
tem-se para o sistema em malha fechada
˙x = Ak ˙x + Bkr,
y = Cx.
Prof. Dr. Alberto Luiz Serpa - 2009 205](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-205-320.jpg)




![Controle de Sistemas em Tempo Cont´ınuo
Exemplo: Seja um duplo integrador dado por
P(s) =
1
s2
.
Deseja-se que a malha fechada com realimenta¸c˜ao de estados seja critica-
mente amortecida com um tempo de estabiliza¸c˜ao a 2% de 2s, e que o erro
estacion´ario ao degrau seja nulo.
A equa¸c˜ao diferencial correspondente ´e
Y (s) =
1
s2
U(s) ⇒ s2
Y (s) = U(s) ⇒ ¨y = u(t).
Sejam os estados x1 = y e x2 = ˙y. Logo escreve-se que
˙x1
˙x2
=
0 1
0 0
x1
x2
+
0
1
u,
y = [1 0]
x1
x2
.
A matriz de controlabilidade neste caso ´e
M = [B AB] =
0 1
1 0
,
cujo determinante ´e
detM = −1,
e conseq¨uentemente tem-se um sistema control´avel.
Os requisitos de projeto s˜ao ξ = 1 e Te2% = 2. Logo,
Te2% =
4
ξwn
⇒ wn =
4
ξTe2%
= 2rad/s.
Portanto, os p´olos desejados s˜ao
µ1,2 = −ξwn ± jwn 1 − ξ2 = −2 ± 0j.
Logo,
φ(s) = (s + 2)(s + 2) = s2
+ 4s + 4.
Aplicando a f´ormula de Ackermann obt´em-se os ganhos da realimenta¸c˜ao
de estados, ou seja,
K = [0 1]M−1
φ(A) =
Prof. Dr. Alberto Luiz Serpa - 2009 210](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-210-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
= [0 1]
0 1
1 0
−1
0 1
0 0
2
+ 4
0 1
0 0
+ 4
1 0
0 1
= [4 4].
Considerando inicialmente kp = 1, a matriz de estado de malha fechada
´e
AK = A − BK =
0 1
0 0
−
0
1
[4 4] =
0 1
−4 −4
,
e a matriz de entrada BK ´e
BK = B =
0
1
.
A resposta ao degrau deste sistema em malha fechada ´e mostrada na
Figura 160, onde se verifica que o valor da resposta de regime ´e 0.25.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.05
0.1
0.15
0.2
0.25
Step Response
Time (sec)
Amplitude
Figura 160: Resposta ao degrau unit´ario para a malha fechada com kp = 1.
Neste caso, ´e necess´ario fazer uma compensa¸c˜ao atrav´es da constante
kp = 4. Inserindo esta constante dentro da malha de controle, a matriz de
entrada passa a ser
B = kp
0
1
=
0
4
.
A matriz de ganhos de realimenta¸c˜ao de estados passa a ser
K =
1
kp
[4 4] = [1 1].
Prof. Dr. Alberto Luiz Serpa - 2009 211](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-211-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
A matriz de estado da malha fechada ´e dada por
AK = A − BK =
0 1
0 0
−
0
4
[1 1] =
0 1
−4 −4
,
e a matriz de entrada BK ´e
BK = B =
0
4
.
A resposta ao degrau da malha fechada ´e apresentada na Figura 161 onde
se verifica a adequada compensa¸c˜ao do erro estacion´ario.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Step Response
Time (sec)
Amplitude
Figura 161: Resposta ao degrau unit´ario para a malha fechada com kp = 4.
A fun¸c˜ao de transferˆencia da malha fechada ´e dada por
Y (s)
R(s)
= C(sI − AK)−1
BK + D =
= [1 0] s
1 0
0 1
−
0 1
−4 −4
−1
0
4
=
= [1 0]
s −1
4 s + 4
−1
0
4
=
4
s2 + 4s + 4
,
que possui o polinˆomio caracter´ıstico desejado.
Prof. Dr. Alberto Luiz Serpa - 2009 212](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-212-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
As margens de estabilidade do sistema controlado podem ser calculadas
empregando-se a fun¸c˜ao de transferˆencia de malha aberta, que ´e relacionada
`as matrizes (A, B, K, D), resultando em margem de ganho infinita e margem
de fase de 76◦
.
A fun¸c˜ao de tranferˆencia equivalente do controlador ´e dada por
Heq(s) =
L(s)
P(s)
= 4s + 4.
O sinal de controle para este exemplo ´e apresentado na Figura 162 e foi
determinado atrav´es da resposta do sistema (Ak, Bk, −K, kp). Note que o
ganho kp foi incorporado `a matriz K neste caso.
0 0.5 1 1.5 2 2.5 3 3.5
2.8
3
3.2
3.4
3.6
3.8
4
Step Response
Time (sec)
Amplitude
Figura 162: Sinal de controle.
Um c´odigo MATLAB para este exemplo ´e apresentado a seguir.
%realimenta¸c~ao de estados - rastreador
clear all; close all; clc;
A=[0 1; 0 0];
B=[0; 1];
C=[1 0];
D=0;
p=ss(A,B,C,D); ps=tf(p); %planta
M=ctrb(A,B) %matriz de controlabilidade
Prof. Dr. Alberto Luiz Serpa - 2009 213](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-213-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
detM=det(M)
qsi=1; te2=2;
wn=4/(qsi*te2)
polosd=[-qsi*wn+wn*sqrt(1-qsi^2) -qsi*wn-wn*sqrt(1-qsi^2)] %polos desejados
K=acker(A,B,polosd) %ganhos da realimenta¸c~ao
%malha fechada
Ak=A-B*K;
Bk=B; Ck=C; Dk=0;
step(Ak,Bk,Ck,Dk)
kp=1/dcgain(Ak,Bk,Ck,Dk)
%compensando o erro estacion´ario na sa´ıda da malha fechada
Ck1=kp*Ck;
figure; step(Ak,Bk,Ck1,Dk)
%compensando o erro estacion´ario na entrada da malha fechada
Bk1=kp*Bk;
figure; step(Ak,Bk1,Ck,Dk)
%compensando o erro dentro da malha
B1=kp*B;
K1=acker(A,B1,polosd) %ou K1=K/kp
Ak=A-B1*K1
Bk=B1; Ck=C; Dk=0;
figure; step(Ak,Bk,Ck,Dk)
[y,x,tempo]=step(Ak,Bk,Ck,Dk); %sa´ıda y e estados x no tempo
t=ss(Ak,Bk,Ck,Dk);
ts=tf(t) %fun¸c~ao de transfer^encia de malha fechada
%margens de estabilidade do sistema controlado
% ls ´e a fun¸c~ao de malha aberta
l=ss(A,B1,K1,D); ls=tf(l);
figure, margin(l)
figure, rlocus(l)
ks=ls/ps; %controlador equivalente
ks=minreal(ks)
figure, step(Ak,Bk,-K1,kp) %sinal de controle
u=-K1*x’+kp*1; %calculo atrav´es da lei de controle
Prof. Dr. Alberto Luiz Serpa - 2009 214](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-214-320.jpg)


![Controle de Sistemas em Tempo Cont´ınuo
O erro e(t) entre os estados reais e os estimados ´e dado por
e = x − ˆx.
Logo, pode-se escrever
˙e = ˙x − ˙ˆx = Ax + Bu − [Aˆx + Bu + L(y − Cˆx)] =
= A(x − ˆx) − LC(x − ˆx),
ou ainda
˙e = (A − LC)e. (17)
Conseq¨uentemente o comportamento dinˆamico do vetor erro ´e determi-
nado pelos autovalores da matriz A − LC. Se os autovalores representarem
uma condi¸c˜ao de estabilidade, ent˜ao o vetor erro sempre convergir´a para zero.
Isso implica que ˆx → x para quaisquer ˆx(0) e x(0). ´E conveniente que os
autovalores de A−LC estejam mais `a esquerda no plano complexo para que
esta convergˆencia seja mais r´apida.
22.1 Malha fechada com observador - regulador
Considere uma realimenta¸c˜ao de estados feita com base no vetor estimado ˆx.
Este problema pode ser resolvido em duas etapas:
• determina¸c˜ao dos ganhos K da realimenta¸c˜ao de estados que aloquem
os p´olos nas posi¸c˜oes desejadas, e
• determina¸c˜ao dos ganhos do observador L para que este seja suficien-
temente r´apido na tarefa de estimar os estados.
Considere a lei de realimenta¸c˜ao de estados do problema de regula¸c˜ao,
u = −Kˆx, com base nos estados estimados.
Malha fechada com base nos estados e no erro
A malha fechada com observador ser´a dada por
˙x = Ax + B(−Kˆx) = Ax − BKˆx = Ax − BKˆx − BKx + BKx,
ou ainda
˙x = (A − BK)x + BKe. (18)
Combinando esta equa¸c˜ao com a equa¸c˜ao do erros tem-se a equa¸c˜ao de
estados com a inclus˜ao do observador
˙x
˙e
=
A − BK BK
0 A − LC
x
e
.
Prof. Dr. Alberto Luiz Serpa - 2009 218](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-218-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
A equa¸c˜ao da sa´ıda ´e dada por
y = Cx + Du = Cx + D(−Kˆx) = Cx − DKˆx + DKx − DKx =
= (C − DK)x + DKe,
ou ainda
y = [C − DK DK]
x
e
.
Os p´olos do sistema com observador podem ser determinados atrav´es da
equa¸c˜ao caracter´ıstica dada por
det
sI − A + BK −BK
0 sI − A + LC
= 0,
det[sI − A + BK]
real. estados
det[sI − A + LC]
observador
= 0.
Verifica-se que os termos associados `a realimenta¸c˜ao de estados e referen-
tes ao onservador s˜ao independentes, caracterizando o princ´ıpio da separa¸c˜ao,
que permite alocar os p´olos da realimenta¸c˜ao de estados de forma indepen-
dente da aloca¸c˜ao de p´olos do observador.
Os p´olos devido `a realimenta¸c˜ao de estados devem ser alocados para aten-
der aos requisitos de desempenho. Os p´olos do observador devem assegurar
que o erro convirja rapidamente a zero, para se ter uma boa estimativa dos
estados que ser˜ao realimentados.
Malha fechada com base nos estados e estados estimados
A malha tamb´em pode ser fechada em termos dos estados x e dos estados
estimados ˆx, ou seja,
˙x = Ax + B(−Kˆx) = Ax − BKˆx.
Substituindo a lei de controle na equa¸c˜ao do observador tem-se que
˙ˆx = Aˆx + B(−Kˆx) + L(Cx + Du − Cˆx − Du),
˙ˆx = Aˆx − BKˆx + LCx − LCˆx,
˙ˆx = (A − BK − LC)ˆx + LCx,
que pode ser colocada na forma matricial como
˙x
˙ˆx
=
A −BK
LC A − BK − LC
x
ˆx
,
Prof. Dr. Alberto Luiz Serpa - 2009 219](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-219-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
e a equa¸c˜ao de sa´ıda ´e
y = Cx + D(−Kˆx) = Cx − DKˆx
ou ainda
y = [C − DK]
x
ˆx
.
22.2 Aloca¸c˜ao de p´olos do observador
A equa¸c˜ao do erro pode ser interpretada como uma aloca¸c˜ao de p´olos da
matriz At
− Ct
Lt
.
A f´ormula de Ackermann neste caso torna-se
Lt
= [0 0 . . . 0 1] Ct
At
Ct
. . . A(n−1)t
Ct −1
ψ(At
)
que requer que a matriz de observabilidade seja invers´ıvel, ou seja,
det Ct
At
Ct
. . . A(n−1)t
Ct
= 0.
Um sistema ´e dito observ´avel se for poss´ıvel determinar o seu estado a
partir da observa¸c˜ao da sa´ıda durante um intervalo de tempo finito.
22.3 Fun¸c˜ao de transferˆencia equivalente para regula-
dor
No caso de um problema de regulador a lei de controle ´e u = −Kˆx. Neste
caso, pode-se escrever a equa¸c˜ao do observador
˙ˆx = Aˆx + Bu + L(y − Cˆx − Du),
˙ˆx = Aˆx − BKˆx + L(y − Cˆx + DKˆx),
ou ainda
˙ˆx = (A − BK − LC + LDK)ˆx + Ly
z = Kˆx
´E poss´ıvel escrever a seguinte fun¸c˜ao de transferˆencia equivalente para o
controlador com observador
Z(s)
Y (s)
= K[sI − (A − BK − LC + LDK)]−1
L,
que pode ser usada juntamente com a fun¸c˜ao de transferˆencia da planta para
definir a malha aberta e analisar as margens de estabilidade.
Prof. Dr. Alberto Luiz Serpa - 2009 220](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-220-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
22.4 Malha fechada com observador - rastreador
Seja a lei de realimenta¸c˜ao de estados u = kp(r − Kˆx) com base nos estados
estimados. A malha fechada com observador ser´a dada por
˙x = Ax + Bkp(r − Kˆx) =
= Ax + kpBr − kpBKˆx = Ax + kpBr − kpBKˆx − kpBKx + kpBKx,
ou ainda
˙x = (A − kpBK)x + kpBKe + kpBr.
Combinando esta equa¸c˜ao com a equa¸c˜ao do erro tem-se na forma matri-
cial
˙x
˙e
=
A − kpBK kpBK
0 A − LC
x
e
+
kpB
0
r
A equa¸c˜ao da sa´ıda ´e dada por
y = Cx + Du = Cx + D[kp(r − Kˆx)] =
= Cx + kpDr − kpDKˆx + kpDKx − kpDKx =
= (C − kpDK)x + kpDKe + kpDr,
ou ainda
y = [C − kpDK kpDK]
x
e
+ kpDr.
A malha tamb´em pode ser fechada em termos dos estados x e dos estados
estimados ˆx, ou seja,
˙x = Ax + B[kp(r − Kˆx)] = Ax − kpBKˆx + kpBr.
Substituindo a lei de controle na equa¸c˜ao do observador tem-se
˙ˆx = Aˆx + B[kp(r − Kˆx) + L(Cx + Du − Cˆx − Du),
˙ˆx = Aˆx + kpBr − kpBKˆx + LCx − LCˆx,
˙ˆx = (A − kpBK − LC)ˆx + kpBr + LCˆx,
que pode ser colocada na forma matricial como
˙x
˙ˆx
=
A −kpBK
LC A − kpBK − LC
x
ˆx
+
kpB
kpB
r
e a equa¸c˜ao de sa´ıda ´e
y = Cx + D[kp(r − Kˆx)] = Cx + kpDr − kpDKˆx
Prof. Dr. Alberto Luiz Serpa - 2009 221](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-221-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
ou ainda
y = [C − kpDK]
x
ˆx
+ kpDr.
Exemplo: Analisar o problema da realimenta¸c˜ao de estados para o se-
guinte modelo:
˙x =
−0.4 0 −0.01
1 0 0
−1.4 9.8 −0.02
x +
6.3
0
9.8
u,
y = [0 0 1]x.
Os p´olos da malha fechada devem ser −1 ± j e −2.
A matriz de realimenta¸c˜ao de estados pode ser obtida com a f´ormula de
Ackermann, ou seja,
K = [0.4706 1.0000 0.0627].
Este sistema em malha fechada apresenta uma resposta de regime de
15.4350. Para que o erro estacion´ario seja nulo, o ganho proporcional e a
matriz de realimenta¸c˜ao de estados devem ser recalculados como
kp =
1
15.4350
e K =
1
kp
[0.4706 1.0000 0.0627] = [7.2644 15.4357 0.9685].
A matriz B deve ser corrigida para
B = kp
6.3
0
9.8
=
0.4082
0
0.6349
.
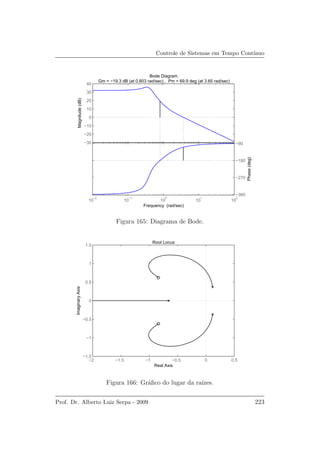
As margens de estabilidade e o lugar das ra´ızes , Figuras 165 e 166, podem
ser obtidos atrav´es da fun¸c˜ao de transferˆencia de malha aberta que ´e dada
por
G(s) = K(sI − A)−1
B + D,
ou seja,
G(s) =
3.58s2
+ 6.006s + 3.902
s3 + 0.42s2 − 0.006s + 0.098
.
A an´alise do diagrama de Bode e do gr´afico do lugar das ra´ızes mostra
uma margem de redu¸c˜ao de ganho de −19.3dB, e verifica-se atrav´es do gr´afico
do lugar das ra´ızes que a margem de ganho ´e infinita. A margem de fase ´e
de 69.9◦
.
Prof. Dr. Alberto Luiz Serpa - 2009 222](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-222-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
A fun¸c˜ao de transferˆencia equivalente do controlador pode ser obtida
atrav´es da divis˜ao da fun¸c˜ao de transferˆencia da malha aberta G(s) pela
fun¸c˜ao de transferˆencia da planta P(s), ou seja,
K(s) =
G(s)
P(s)
=
0.3653s2
+ 0.6129s + 0.3982
s2 − 0.5s + 6.3
.
O efeito da inclus˜ao de um observador com p´olos −3 ± −3j e −4 ´e ana-
lisado a seguir. A matriz de realimenta¸c˜ao do observador ´e
L = [5.4664 4.6762 9.5800]′
.
Para o caso de regulador, as margens de estabilidade e o gr´afico do lugar
das ra´ızes s˜ao apresentados nas Figuras 167 e 168.
−60
−40
−20
0
20
40
60
Magnitude(dB)
10
−2
10
−1
10
0
10
1
10
2
10
3
−360
−315
−270
−225
−180
−135
−90
Phase(deg)
Bode Diagram
Gm = −12.1 dB (at 2.42 rad/sec) , Pm = 21.4 deg (at 33.2 rad/sec)
Frequency (rad/sec)
Figura 167: Diagrama de Bode com observador.
A malha fechada considerando o observador pode ser fechada em termos
dos estados estimados e dos erros das estimativas. Em ambos os casos os p´olos
de malha fechada s˜ao: −2.0, −1.0 ± 1.0j, −4.0 e −3.0 ± 3.0j verificando-se
as especifica¸c˜oes desejadas.
As respostas ao degrau do sistema com e sem observador para condi¸c˜oes
iniciais nulas s˜ao identicas, j´a que o observador acompanha de forma exata
Prof. Dr. Alberto Luiz Serpa - 2009 224](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-224-320.jpg)
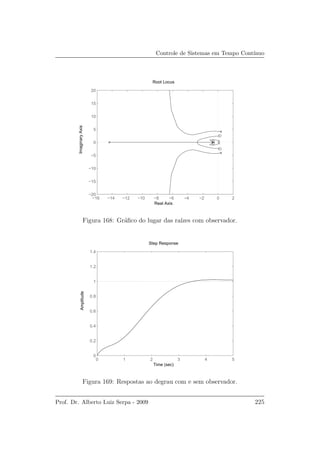
![Controle de Sistemas em Tempo Cont´ınuo
os estados pois n˜ao h´a qualquer erro inicial. Este resposta ´e mostrada na
Figura 169.
Para o caso de regulador com uma condi¸c˜ao inicial n˜ao nula ´e poss´ıvel
verificar o desempenho do observador. As Figuras 170, 171 e 172 mostram
os estados e suas estimativas feitas pelo observador considerando a seguinte
condi¸c˜ao inicial: x0 = [1 2 3] e ˆx0 = [−1 − 2 − 3].
0 0.5 1 1.5 2
−6
−5
−4
−3
−2
−1
0
1
2
3
Figura 170: x1 e ˆx1.
Um c´odigo MATLAB para este exemplo ´e apresentado a seguir.
clear all; close all; clc;
%modelo de estados
a=[-0.4 0 -0.01; 1 0 0; -1.4 9.8 -0.02];
b=[6.3 0 9.8]’;
c=[0 0 1];
d=0;
p=ss(a,b,c,d);
%funcao de transferencia da planta
ps=tf(p)
Prof. Dr. Alberto Luiz Serpa - 2009 226](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-226-320.jpg)
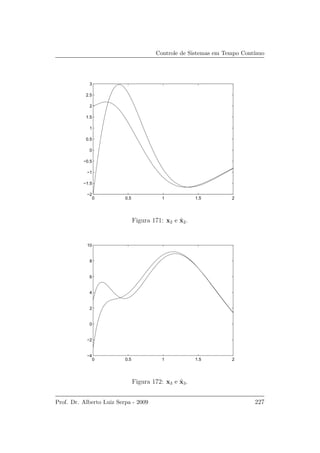
![Controle de Sistemas em Tempo Cont´ınuo
%polos e zeros
[pp,zp]=pzmap(p)
%verificacao da controlabilidade
mc=ctrb(a,b);
detc=det(mc)
%polos desejados
pd=[-1+j -1-j -2];
%ganhos da realimentacao de estados
k=place(a,b,pd)
%funcao de transferencia da malha aberta sem observador
g=ss(a,b,k,d);
gs=tf(g)
%funcao de transferencia do compensador sem observador
ks=gs/ps;
ks=minreal(ks)
%polos e zeros do compensador sem observador
[pk,zk]=pzmap(ks)
%malha fechada sem observador e sem compensar
%o erro estacionario
ak=a-b*k;
bk=b;
ck=c;
dk=d;
t=ss(ak,bk,ck,dk);
ts=tf(t)
dct=dcgain(t)
%resposta ao degrau sem observador e
%sem compensar o erro estacionario
step(t,’k’)
%compensando o erro estacionario sem obervador
kp=1/dct
b=kp*b; %kp incorporado em b
Prof. Dr. Alberto Luiz Serpa - 2009 228](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-228-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
k=k/kp; %ou k=place(a,b,pd)
ak=a-b*k;
bk=b;
figure
t1=ss(ak,bk,ck,dk);
ts1=tf(t1);
step(t1,’k’)
%lugar das raizes
figure
rlocus(g,’k’)
%margens de estabilidade sem observador
figure
margin(g)
%verificacao da observabilidade
mo=obsv(a,c);
deto=det(mo)
%polos e zeros de malha fechada sem observador
[pt,zt]=pzmap(t)
%polos do observador
po=[-3+3*j -3-3*j -4];
%ganhos do observador
l=place(a’,c’,po);
l=l’
%funcao de tranferencia do compensador com observador
%pressupoe regulador (util apenas para calcular
%as margens de estabilidade).
ac=a-b*k-l*c+l*d*k;
bc=l;
cc=k;
dc=0;
ko=ss(ac,bc,cc,dc);
kos=tf(ko);
kos=minreal(kos)
[pkos,zkos]=pzmap(ko)
Prof. Dr. Alberto Luiz Serpa - 2009 229](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-229-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
%comando direto para obter o modelo
%de estado do compensador (regulador)
[ac1,bc1,cc1,dc1]=reg(a,b,c,d,k,l)
ko1=ss(ac1,bc1,cc1,dc1);
kos1=tf(ko1)
%malha aberta com observador (regulador)
gco=p*ko;
figure
rlocus(gco,’k’)
figure
margin(gco)
%malha fechada em termos do erro do observador
ae=[a-b*k b*k; zeros(size(a)) a-l*c];
be=[b; zeros(size(b))];
ce=[c-d*k d*k];
de=d;
te=ss(ae,be,ce,de);
tes=tf(te)
[pte,zte]=pzmap(te)
dcte=dcgain(te)
%malha fechada em termos dos estados estimados pelo observador
ax=[a -b*k; l*c a-b*k-l*c];
bx=[b; b];
cx=[c -d*k];
dx=d;
tx=ss(ax,bx,cx,dx);
txs=tf(tx)
[ptx,ztx]=pzmap(tx)
dctx=dcgain(tx)
%comparacao das respostas ao degrau
figure
step(t1,’k’,te,’k’,tx,’k’)
%verificacao sob condicoes iniciais distintas
%aumentando o modelo de estados com os estados
x0=[1 2 3];
Prof. Dr. Alberto Luiz Serpa - 2009 230](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-230-320.jpg)
![Controle de Sistemas em Tempo Cont´ınuo
xx0=[-1 -2 -3];
[axa,bxa,cxa,dxa]=augstate(ax,bx,cx,dx);
txa=ss(axa,bxa,cxa,dxa);
time=0:0.01:2;
resp=initial(txa,[x0 xx0],time);
figure
plot(time,resp(:,2),’k’,time,resp(:,5),’k’)
figure
plot(time,resp(:,3),’k’,time,resp(:,6),’k’)
figure
plot(time,resp(:,4),’k’,time,resp(:,7),’k’)
23 Bibliografia
1. Shahian B., Hassul M., Control System Design Using Matlab, Prentice-
Hall, 1993.
2. Ogata K., Engenharia de Controle Moderno, Pearson / Prentice-Hall,
2003.
3. Wilkie J., Johnson M., Katebi R., Control Engineering - An introduc-
tory course, Palgrave, 2002.
4. Sinha N. K., Linear Systems, John Wiley & Sons, 1991.
5. Bottura C. P., An´alise Linear de Sistemas, Guanabara Dois, 1982.
Prof. Dr. Alberto Luiz Serpa - 2009 231](https://image.slidesharecdn.com/textoem7071-160520065722/85/sumando-1-2-3-231-320.jpg)






