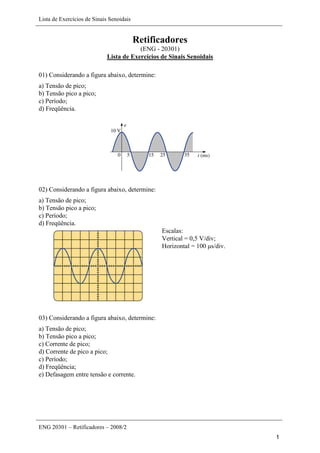
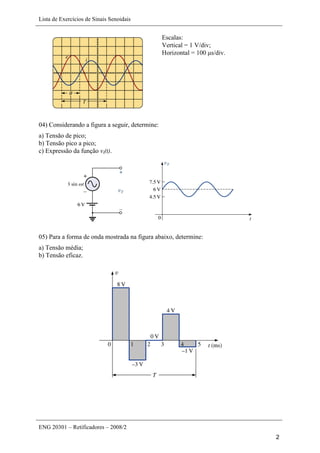
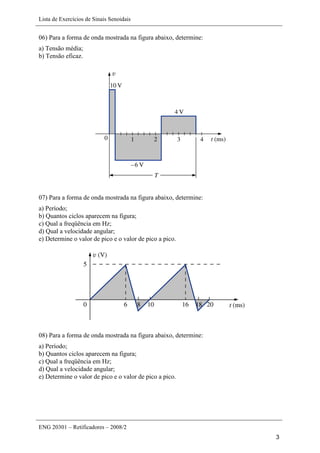
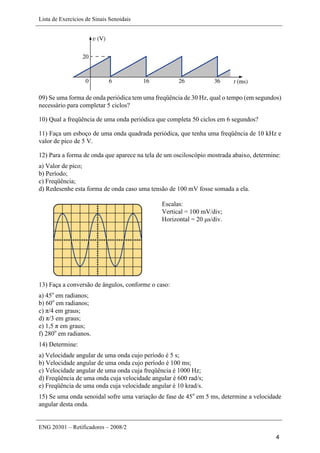
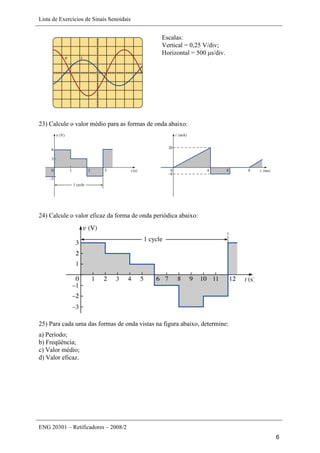
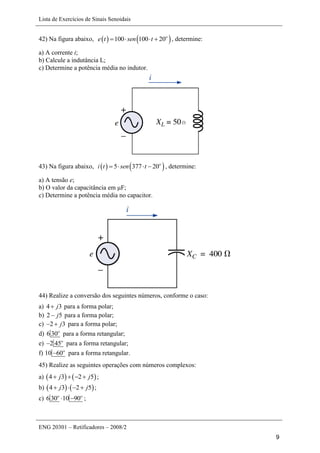
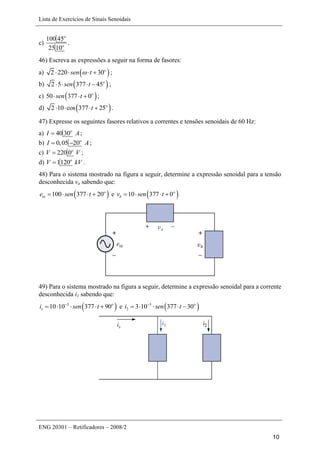
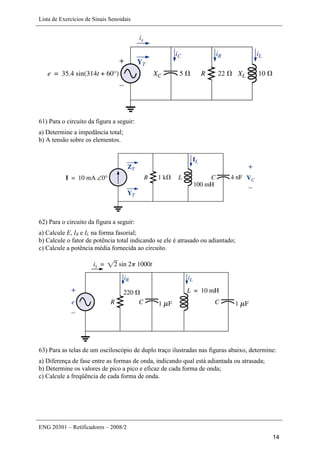
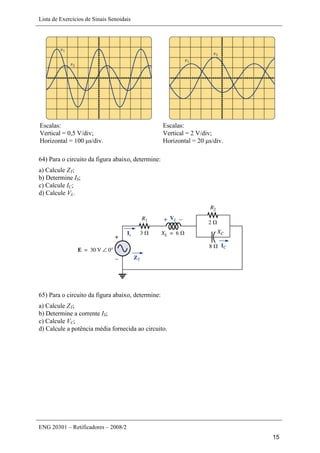
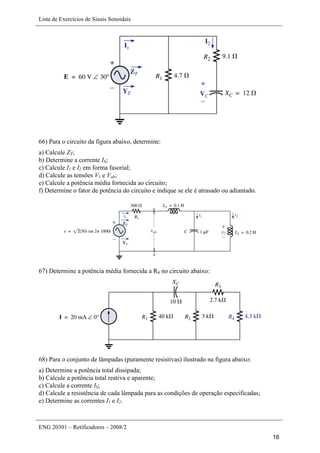
Este documento apresenta uma lista de 45 exercícios relacionados a sinais senoidais, incluindo determinação de parâmetros de formas de onda, conversão entre ângulos e radianos, cálculo de reatâncias em indutores e capacitores, e operações com números complexos. As questões envolvem análise de sinais senoidais em osciloscópios, cálculo de período, frequência, valor de pico, entre outros parâmetros.