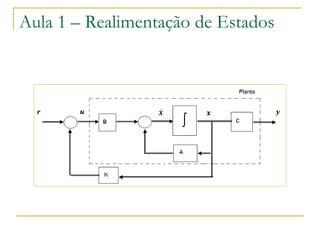
O documento discute realimentação de estados em sistemas de controle. Apresenta como reposicionar os pólos da malha fechada alterando o ganho K e como isso pode afetar a observabilidade do sistema, criando ou destruindo esta propriedade. Também fornece a fórmula de Ackermann para calcular K e exemplos no MatLab ilustrando os conceitos.

1. Controle Avançado – 2011-I Prof. Marcos Cruz

2. Aula 1 – Realimentação de Estados Realimentação de estados x : as variáveis de estado do sistema precisam estar disponíveis para serem utilizadas pelo controlador; Realimentação de saídas y : um conjunto de variáveis de saída relacionadas a variáveis de estado devem estar disponíveis, y = Cx+Du;

3. Aula 1 – Realimentação de Estados

4. Aula 1 – Realimentação de Estados Planta: Sistema Realimentado Controle

5. Aula 1 – Realimentação de Estados Os pólos em malha fechada serão os autovalores de (A – BK) e podem ser posicionados arbitrariamente se e somente se o par (A,B) for controlável; Obs: sI – (A – BK) = sI – A + BK

6. Exemplo

7. Exemplo - continuação

8. Vantagem da Forma Canônica Controlável A imposição de uma dinâmica modificada para o sistema (em outro termos, reposicionamento dos pólos da malha fechada em relação aos pólos da malha aberta) é simplificado pela representação do sistema na forma controlável, porque pode se escolher uma lei de controle u(t) que altere todos coeficientes da matriz dinâmica;

9. Exemplo no MatLab Os comandos ‘place’ e ‘acker’ retornam o vetor K, com os ganhos necessários para que os autovalores em malha fechada se posicionem onde especificado;

10. Exemplo – no MatLaB >> f=place(A,B,[-2+3.464j,-2-3.464j]) f = 13.9993 1.0000 >> f=acker(A,B,[-2+3.464j,-2-3.464j]) f = 13.9993 1.0000

11. Exemplo – quando não é possível reposicionar um dos autovalores O autovalor +2 não pode ser reposicionado porque o termo correspondente na matriz sI – (A-BK) não pode ser alterado por K 1 nem por K 2 ; O termo ‘fixo’ é ‘s-2’;

12. Exemplo Anterior – identificando um modo não controlável >> [P,AV]=eig(A) P = 1.0000 0.7071 0 0.7071 AV = 1 0 0 2 >> Pinv = inv(P) Pinv = 1.0000 -1.0000 0 1.4142 >> Bstar = Pinv*B Bstar = 1 0

13. Exemplo Anterior – identificando um modo não controlável O zero na matriz modal B mostra que o modo associado ao estado r 2 não é controlável;

14. Fórmula de Ackermann Para sistemas com ordem maior que 2, a fórmula de Ackermann provê uma maneira mais simples de determinar os valores de K; Q = [A AB …A n-1 B] matriz de controlabilidade; K = [0…1]Q -1  d (A)  d (s): polinômio definido pela localização dos novos pólos;

15. Fórmula de Ackermann – voltando ao exemplo

16. Ackermann – Função p/ evoluir polinômio c/ argumento matriz quadrada >> P=[1 4 16]; >> A=[0 1;-2 -3]; >> Y=POLYVALM(P,A) Y = 14 1 -2 11 1,4,16 coeficientes de s 2 +4s+16; 3 coeficientes porque grau máximo (no caso) é 2; Atenção: POLYVAL ≠ POLYVAL M;

17. Restrições Numéricas ao comando ‘acker’ Note: This algorithm uses Ackermann's formula. This method is NOT numerically reliable and starts to break down rapidly for problems of order greater than 10, or for weakly controllable systems. A warning message is printed if the nonzero closed-loop poles are greater than 10% from the desired locations specified in P.

18. Realimentação de Estados – efeito sobre a observabilidade Realimentação de estados não modifica a controlabilidade, mas pode afetar a observabilidade, criando ou destruindo esta; A destruição da observabilidade está associada ao deslocamento de um pólo que, em função disso, cancela um zero;

19. Exemplo – efeito sobre observabilidade O=OBSV(A,C) O = 1 1 4 -1 >> rank(O) ans = 2

20. Exemplo – efeito sobre observabilidade Autovalores de A: 2.61 e 0.38 (instável); Projeto de realimentação para posicionar os autovalores em -1 e -2; O posicionamento em -1 deverá comprometer a observabilidade; >> f=place(A,B,[-1,-2]) f = 6.0000 1.0000; Ã=(A-BK) Ã = [-3 -2;1 0];

21. Exemplo – efeito sobre observabilidade Autovalores de A: 2.61 e 0.38 (instável); Projeto de realimentação para posicionar os autovalores em -1 e -2; O posicionamento em -1 deverá comprometer a observabilidade; >> Atil= [-3 -2;1 0]; >> C=[1 1]; >> O=OBSV(Atil,C) O = 1 1 -2 -2 >> rank(O) ans = 1

22. Exercício A = (1 1;1 2) B = (1;0) Verificar estabilidade (instabilidade, no caso) Projetar ganho de realimentação de estados que estabiliza o sistema; Se novos autovalores em -5 e -6, K = [14 57]; Verificar se a Observabilidade foi afetada;