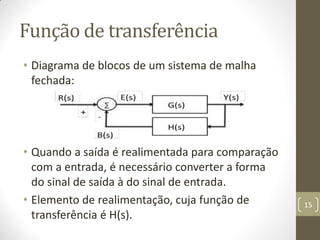
O documento discute modelos matemáticos para sistemas dinâmicos, incluindo sistemas lineares e não lineares. Ele também explica funções de transferência, que caracterizam as relações de entrada e saída de sistemas lineares invariantes no tempo, e como elas podem ser usadas para análise e projeto desses sistemas. Diagramas de blocos são apresentados como uma forma de representar funções de transferência.

1. Estudos de Controle
– Modelagem (1)
1

2. Modelos Matemáticos
• Modelagem matemática de sistemas dinâmicos:
• Analisar características dinâmicas.
• São conjuntos de equações que representam
com precisão ou razoavelmente bem a dinâmica
do sistema.
• Não é único. Geralmente utilizam-se equações
diferenciais.
• É considerada a parte mais importante da análise
de sistemas de controle.
2

3. Propriedades
• Sistemas lineares:
• Definição: um sistema é dito linear se o
princípio da superposição se aplicar a ele. Ou
seja, a resposta produzida pela aplicação
simultânea de duas funções diversas é a soma
das duas respostas individuais.
• Nesses sistemas, a resposta para cada entrada
pode ser calculada tratando uma de cada vez e
somando o resultado.
• Geralmente, se causa e efeito são
proporcionais, o sistema é linear. 3

4. Propriedades
• Sistemas lineares invariantes no tempo:
• Os sistemas dinâmicos cujos coeficientes das
equações diferenciais são constantes são
chamados de sistemas lineares invariantes no
tempo.
• Exemplo: termostato.
• Sistemas lineares variantes no tempo:
• São os sistemas cujos coeficientes das
equações diferenciais variam no tempo.
• Exemplo: veículo espacial (massa).
4

5. Função de transferência
• Caracterizam as relações de entrada e saída dos
sistemas.
• Geralmente escritas por equações diferenciais
lineares invariantes no tempo.
• Definição: relação entre a transformada de
Laplace da saída (função de resposta) e a
transformada de Laplace da entrada (função de
excitação), admitindo-se as condições iniciais
nulas.
5

6. Função de transferência
• Dada a equação diferencial de um sistema linear
invariante no tempo:
𝑎0
𝑑 𝑛 𝑦
𝑑𝑡 𝑛 + 𝑎1
𝑑 𝑛−1 𝑦
𝑑𝑡 𝑛−1 + … + 𝑎 𝑛−1
𝑑𝑦
𝑑𝑡
+ 𝑎 𝑛 𝑦 =
𝑏0
𝑑 𝑚 𝑥
𝑑𝑡 𝑚 + 𝑏1
𝑑 𝑚−1 𝑥
𝑑𝑡 𝑚−1 + ⋯ + 𝑏 𝑚−1
𝑑𝑥
𝑑𝑡
+ 𝑏 𝑚 𝑥
onde 𝑛 ≥ 𝑚, y é a saída do sistema e x é a entrada.
Então, a função de transferência é
𝐺 𝑠 =
𝑌(𝑠)
𝑋(𝑠)
=
𝑏0 𝑠 𝑚 + 𝑏1 𝑠 𝑚−1 + ⋯ 𝑏 𝑚−1 𝑠 + 𝑏 𝑚
𝑎0 𝑠 𝑛 + 𝑎1 𝑠 𝑛−1 + ⋯ 𝑎 𝑛−1 𝑠 + 𝑎 𝑛 6

7. Função de transferência
• Muito utilizada na análise e projeto de sistemas
lineares invariantes no tempo.
• É um método operacional para expressar a
equação diferencial que relaciona a variável de
saída à variável de entrada.
• É uma propriedade inerente ao sistema,
independentemente da magnitude e da natureza
da função de entrada.
• Não fornece nenhuma informação relativa à
estrutura física do sistema. 7

8. Função de transferência
• Permite estudar a saída do sistema para várias
maneiras de entrada, fornecendo informações
da natureza do sistema.
• Se a função de transferência não é conhecida,
ela pode ser determinada experimentalmente
com o auxílio de entradas conhecidas e análise
das respectivas respostas do sistema.
8

9. Função de transferência
• Exemplo:
• Sistema de controle de posição de um satélite,
considerando apenas um eixo. Dois jatos
localizados em A e B aplicam força de reação
para girar o corpo, com empuxo igual a
𝐹
2
e o
torque resultante seja T=Fl.
9

10. Função de transferência
• Exemplo:
• Como os jatos são aplicados por um certo
tempo, o torque é uma função do tempo 𝑇 𝑡 .
• O momento de inércia em relação ao eixo de
rotação no centro da massa é J.
• Obtenha a função de transferência admitindo
que a entrada é o torque 𝑇 𝑡 e o
deslocamento angular 𝜃(𝑡) é a saída.
10

11. Função de transferência
• Exemplo:
• Aplicando a segunda lei de Newton:
𝑇 𝑡 = 𝐽
𝑑2 𝜃(𝑡)
𝑑𝑡2
• Transformada de Laplace:
𝑇 𝑠 = 𝐽𝑠2
𝜃(𝑠)
• Função de transferência:
𝐺 𝑠 =
𝜃(𝑠)
𝑇 (𝑠)
=
1
𝐽𝑠2
11

12. Função de transferência
• Integral de Convolução
• Dada a função de transferência, podemos
escrevê-la também da seguinte forma
𝑌 𝑠 = 𝐺 𝑠 𝑋(𝑠)
• Que equivale no domínio do tempo a integral
de convolução
𝑦 𝑡 = 𝑔 𝑡 − 𝜏 𝑥 𝜏 𝑑𝜏
𝑡
0
12

13. Função de transferência
• Função de resposta impulsiva:
• A saída de um sistema a um impulso unitário
com condições iniciais nula é dado por
𝑌 𝑠 = 𝐺(𝑠)
• No domínio do tempo g(t) é chamada de
função de resposta impulsiva, que também é
chamada de função característica do sistema.
• Logo, é possível obter informações sobre as
características dinâmicas do sistema por meio
da excitação por um impulso de entrada. 13

14. Função de transferência
• Diagrama de blocos:
• Representação gráfica das funções
desempenhadas por cada componente e o
fluxo de sinais entre eles.
• Blocos funcionais – símbolo da operação
matemática aplicada ao sinal de entrada do
bloco, produzindo uma saída.
• Somador e ponto de ramificação.
14
G(s)

15. Função de transferência
• Diagrama de blocos de um sistema de malha
fechada:
• Quando a saída é realimentada para comparação
com a entrada, é necessário converter a forma
do sinal de saída à do sinal de entrada.
• Elemento de realimentação, cuja função de
transferência é H(s).
15

16. Função de transferência
• Função de transferência de malha aberta:
• Relação entre o sinal de realimentação e o
sinal de erro atuante.
𝐵(𝑠)
𝐸(𝑠)
= 𝐺 𝑠 𝐻(𝑠)
• Função de transferência do ramo direto:
• Relação entre o sinal de saída e o sinal de erro
atuante.
𝐶(𝑠)
𝐸(𝑠)
= 𝐺 𝑠 16

17. Função de transferência
• Malha fechada
• Relaciona o sinal de saída e o sinal de entrada.
𝐶(𝑠)
𝑅(𝑠)
=
𝐺(𝑠)
1 + 𝐺 𝑠 𝐻(𝑠)
17

18. Obrigada!
ays@icmc.usp.br
www.lsec.icmc.usp.br
18