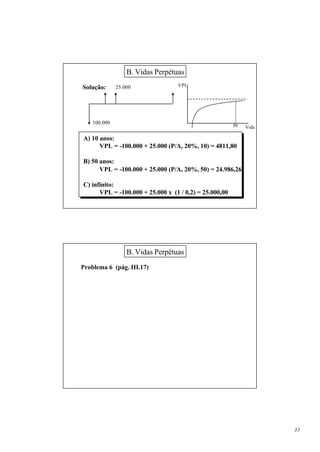
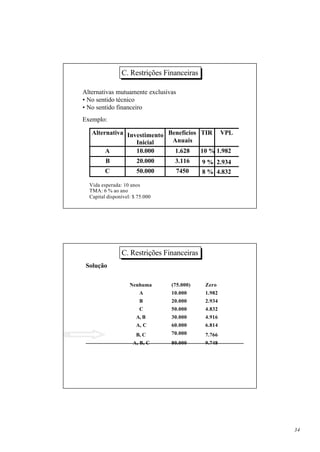
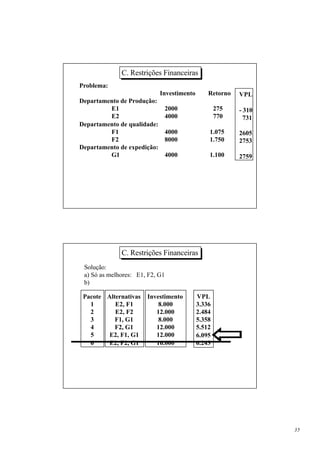
1. O documento apresenta um curso de engenharia econômica ministrado por dois professores que tem como objetivo capacitar os participantes a analisar a viabilidade econômica e financeira de investimentos.
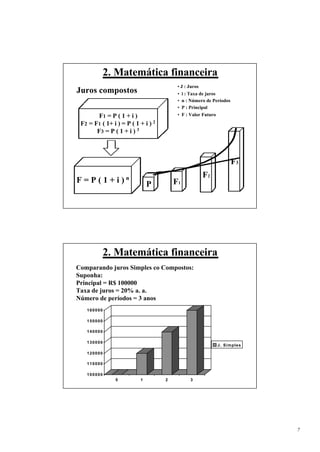
2. A matemática financeira é apresentada como fundamental para a análise de investimentos, abordando conceitos como juros simples, juros compostos e fluxo de caixa.
3. São discutidos critérios para análise de projetos como Payback, Valor Presente Líquido, Taxa Interna de Retorno e a Tax






![2. Matemática financeira
EXEMPLO II.2
SOLUÇÃO:
F = P ( 1 + i 35 dias) 1 (1) F = P ( 1 + idiário) 35 (2)
(1) = (2)
P ( 1 + i 35 dias) 1 = P ( 1 + idiário) 35
( 1 + 0,0306) 1 = ( 1 + idiário) 35 idiário= 0,08615%
( 1 + i 30 dias) 1 = ( 1 + idiário) 30 imensal = 2,617%
Poupança para o dia 17/11 2,39633%
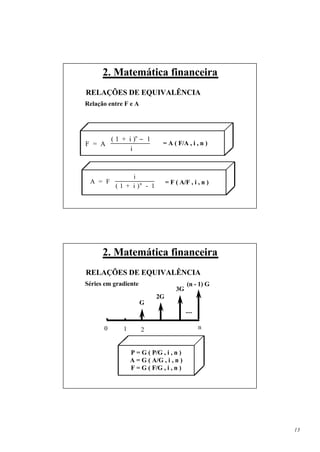
2. Matemática financeira
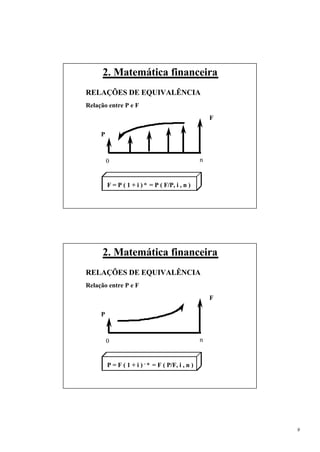
RELAÇÕES DE EQUIVALÊNCIA
Relação entre P e A
P A A
A A A
0 n
P = A ( 1 + i ) - 1 + A ( 1 + i ) - 2+ . . . + A ( 1 + i ) - n
P = A [ ( 1 + i ) -1 + ( 1 + i ) -2 + . . . + ( 1 + i ) -n]
11](https://image.slidesharecdn.com/eeanaliseinvestimento-100815100406-phpapp02/85/Ee-analise-investimento-11-320.jpg)
![2. Matemática financeira
RELAÇÕES DE EQUIVALÊNCIA
Relação entre P e A
( 1 + i )n − 1
P = A n = A ( P/A , i , n )
(1 + i) i
( 1 + i )n i
A = P n = P ( A/P , i , n )
( 1 + i ) - 1
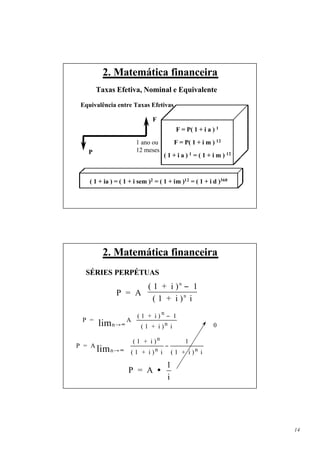
2. Matemática financeira
RELAÇÕES DE EQUIVALÊNCIA
Relação entre F e A
F
A A A A A
0 n
F = A + A ( 1 + i ) 1 + A ( 1 + i ) 2 + . . . + A ( 1 + i ) n-1
F = A [ 1 + ( 1 + i ) 1 + ( 1 + i ) 2 + . . . + ( 1 + i ) n-1 ]
12](https://image.slidesharecdn.com/eeanaliseinvestimento-100815100406-phpapp02/85/Ee-analise-investimento-12-320.jpg)





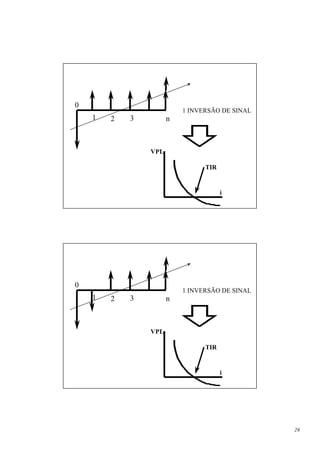
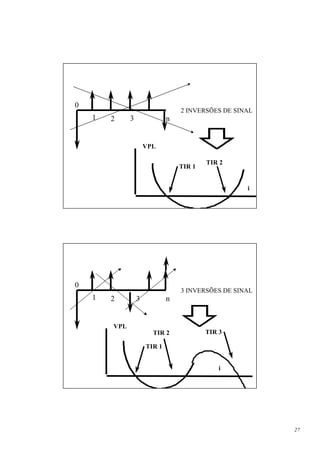
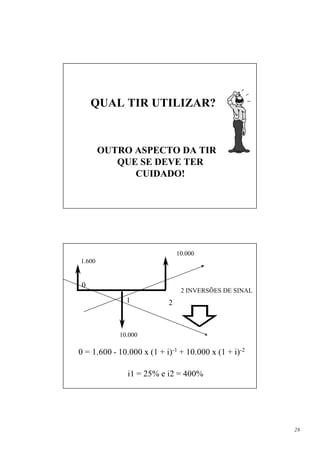
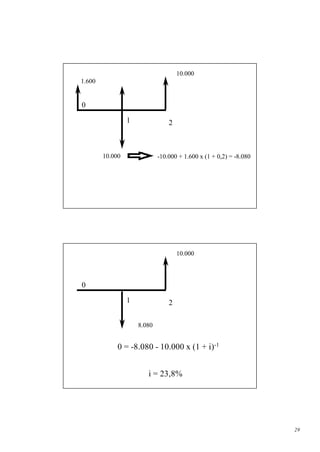

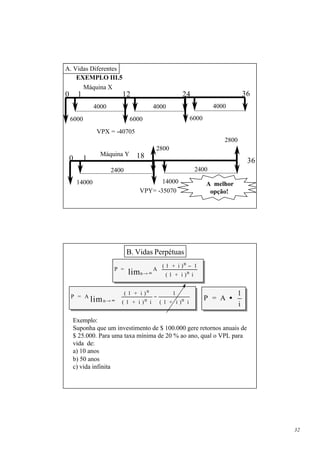
![A. Vidas Diferentes
EXEMPLO III.5
MMC (12, 18) = 36
Máquina X
0 1 12 24 36
4000 4000 4000
6000 6000 6000
VPX = -6000[1+(P/F,12%,12)+(P/F,12%,24)]-4000(P/A, 12%,36)
VPX = -40705
A. Vidas Diferentes
EXEMPLO III.5
2800
2800
Máquina Y 18
0 1 36
2400 2400
14000 14000
VPY= -14000[1+(P/F, 12%, 18)]-2400(P/A, 12%,36)+
+2800[(P/F,12%,18)+(P/F,12%,36)]
VPY= -35070
31](https://image.slidesharecdn.com/eeanaliseinvestimento-100815100406-phpapp02/85/Ee-analise-investimento-31-320.jpg)