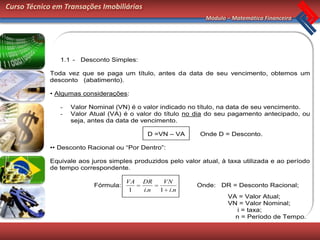
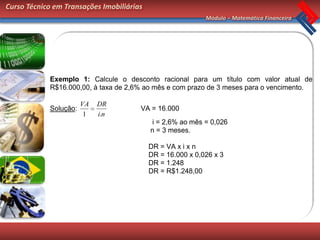
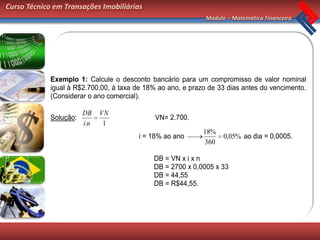
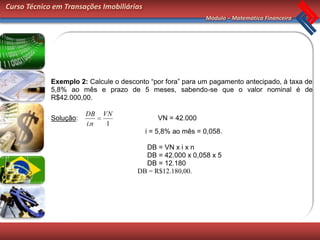
Este documento apresenta os conceitos básicos de matemática financeira sobre capitalização simples, incluindo juros simples, montante simples e desconto simples. Exemplos ilustram como calcular esses valores usando as fórmulas apropriadas. O documento conclui com exercícios de fixação para os alunos praticarem os conceitos apresentados.

1. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
MATEMÁTICA FINANCEIRA
Prof. Ms. Paulo Eduardo Durão Rodrigues
AULA 04

2. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
5. CAPITALIZAÇÃO SIMPLES
No regime de capitalização simples temos, a taxa ( i ) incidindo somente sobre o
capital inicial ( C ), proporcionando-nos obter assim, juros simples, ao final do
período de tempo( n ).
1.1 - Juros Simples:
.i x C = J :opmet ed odoírep mu ed lanif oa C latipac olep odizudorp oruJ ‫٭‬
oa C latipac olep odizudorp oruJ ‫٭‬final de n ( vários ) períodos de tempo: J = C x i x
n.
Fórmula Básica: J = C x i x n Onde: J = juros simples.
C = capital inicial ou principal.
i = taxa de juros.
n = tempo de aplicação ou prazo de
tempo.

3. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 1: Se um capital de R$8.825,00 for aplicado durante 2 meses, à taxa de
2% ao mês, qual será o valor dos juros simples?
Solução: J = C x i x n
C = 8825 J = 8825 x 0,02 x 2
i = 2% ao mês = 0,02 J = 353
n = 2 meses J = R$353,00
Obs: i e n estão na mesma unidade de tempo.
Exemplo 2: Se um capital de R$550,00 for aplicado durante 4 meses, à taxa de 9%
ao ano, qual será o valor dos juros simples?
Solução: J = C x i x n.
C = 550.
9%
i = 9% ao ano 0,75% ao mês = 0,0075.
12
n = 4 meses.
J = 550 x 0,0075 x 4.
J = 16,50.
J = R$16,50.

4. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 3: Calcule o capital necessário para que haja um rendimento de
R$650,00, sabendo-se que a taxa utilizada é de 5% ao mês e o período de tempo
igual a 6 meses.
J
Solução: J = C x i x n, mas isolando-se C temos, C =
i.n
J = 650.
650
i = 5% ao mês = 0,05. C=
0,05 * 6
n = 6 meses. C = 2166,67.
C = R$2.166,67.

5. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 4: Um capital de R$425,00 foi aplicado durante 6 meses, rendendo
R$105,00 de juros simples. Calcule a taxa mensal i.
J
Solução: J = C x i x n, mas isolando-se i temos, i = .
C.n
J = 105.
105
C = 425. i=
425 * 6
n = 6 meses. i = 0,04117
i = 0,04117 está na forma unitária. Para colocarmos o
resultado na forma percentual devemos multiplicar i por
100, ficando então como resposta, i = 4,117% ao mês.
Na taxa i a unidade de tempo utilizada foi o mês
porque o período de aplicação estava, em meses.

6. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
1.1 - Montante Simples:
À soma dos juros simples (relativo ao período de aplicação) com o capital inicial ou
principal dá-se o nome de montante simples.
Fórmulas: S = J + C ou S=Cxixn+C
S = C x ( i x n + 1)
Onde: S = Montante Simples.
J = Juros Simples.
i = Taxa de Juros.
n = Período de Aplicação.

7. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 1: Um capital de R$1.550,00 foi aplicado durante um período de 8 meses,
à taxa de 24% ao ano, no regime de capitalização simples. Calcule o montante.
Solução: S = J + C
C = 1550.
24%
i = 24% ao ano 2% ao mês = 0,02.
12
n = 8 meses.
J = C x i x n.
J = 1550 x 0,02 x 8.
J = 248.
S = J + C.
S = 248 + 1550.
S = 1798.
S = R$1.798,00.

8. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 2: Calcule o tempo, no qual, devo aplicar uma quantia de R$200.000,00,
para obter um montante simples de R$360.000,00, à taxa de 16% ao mês.
Solução: C = 200.000. S = C x (i x n + 1)
S
S = 360.000. (ixn+1)=
C
360.000
i = 16% ao mês = 0,16. (i x n + 1) =
200.000
(i x n + 1) = 1,8.
i x n = 1,8 – 1.
i x n = 0,8.
0,16 x n = 0,8.
n = 5 meses.
A unidade utilizada para n foi meses, devido ao fato, de i
também estar em meses.

9. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
1.1 - Desconto Simples:
Toda vez que se paga um título, antes da data de seu vencimento, obtemos um
desconto (abatimento).
• Algumas considerações:
- Valor Nominal (VN) é o valor indicado no título, na data de seu vencimento.
- Valor Atual (VA) é o valor do título no dia do seu pagamento antecipado, ou
seja, antes da data de vencimento.
D =VN – VA Onde D = Desconto.
•• Desconto Racional ou “Por Dentro”:
Equivale aos juros simples produzidos pelo valor atual, à taxa utilizada e ao período
de tempo correspondente.
VA DR VN
Fórmula: Onde: DR = Desconto Racional;
1 i.n 1 i.n
VA = Valor Atual;
VN = Valor Nominal;
i = taxa;
n = Período de Tempo.

10. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 1: Calcule o desconto racional para um título com valor atual de
R$16.000,00, à taxa de 2,6% ao mês e com prazo de 3 meses para o vencimento.
VA DR
Solução: VA = 16.000
1 i.n
i = 2,6% ao mês = 0,026
n = 3 meses.
DR = VA x i x n
DR = 16.000 x 0,026 x 3
DR = 1.248
DR = R$1.248,00

11. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 2: Se um empréstimo com valor atual de R$750,00, calcule o desconto
racional, sabendo-se que a taxa de juros é de 12% ao ano e o prazo é de 5 meses
para o vencimento.
VA DR
Solução: VA = 750.
1 i.n
12%
i = 12% ao ano 1% ao mês = 0,01.
12
DR = VA x i x n
DR = 750 x 0,01 x 5
DR = 37,5
DR = R$37,5.

12. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
•• Desconto Bancário ou Comercial ou “Por Fora”:
Equivale aos juros simples produzidos pelo valor nominal, à taxa utilizada e ao
período de tempo correspondente.
VA DB VN
Fórmula: Onde: DB = Desconto
1 i.n i.n 1
Bancário;
VA = Valor Atual;
VN = Valor Nominal;
i = Taxa;
n = Período de
Tempo.

13. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 1: Calcule o desconto bancário para um compromisso de valor nominal
igual à R$2.700,00, à taxa de 18% ao ano, e prazo de 33 dias antes do vencimento.
(Considerar o ano comercial).
DB VN
Solução: VN= 2.700.
i.n 1
18%
i = 18% ao ano 0,05% ao dia = 0,0005.
360
DB = VN x i x n
DB = 2700 x 0,0005 x 33
DB = 44,55
DB = R$44,55.

14. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Exemplo 2: Calcule o desconto “por fora” para um pagamento antecipado, à taxa de
5,8% ao mês e prazo de 5 meses, sabendo-se que o valor nominal é de
R$42.000,00.
DB VN
Solução: VN = 42.000
i.n 1
i = 5,8% ao mês = 0,058.
DB = VN x i x n
DB = 42.000 x 0,058 x 5
DB = 12.180
DB = R$12.180,00.

15. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
• Considerações finais dentro da capitalização simples:
-Como se calcular uma taxa acumulada (ao ano) que é aplicada pelo período de n
meses:
Exemplo: No regime de capitalização simples, calcular a taxa acumulada a 36% ao
ano, aplicada durante 8 meses.
Solução: 1º) Verifica-se a taxa, neste caso i =36% ao ano;
2º) Verifica-se o número de meses de aplicação, neste exemplo são 8
meses;
3º) Calcula-se o valor da taxa i no mês;
36%
ex.: 3% ao mês.
12
4º) Multiplica-se a taxa encontrada pelo número de meses;
ex.: 3% x 8 = 24%.
5º) Resultado Final: 24%.

16. Curso Técnico em Transações Imobiliárias
Módulo – Matemática Financeira
Chegamos ao final desta aula.
Resolva os exercícios de fixação propostos logo abaixo.
Quaisquer dúvidas, acionar o tutor por meio do Bate Papo.
BONS ESTUDOS MEUS CAROS.
ATÉ A PRÓXIMA AULA.