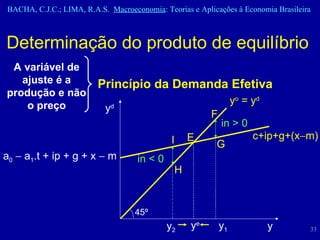
1) O documento discute modelos macroeconômicos simplificados de determinação da renda agregada. 2) Dois modelos são apresentados, onde o consumo depende da renda disponível e a poupança é definida residuamente. 3) Estes modelos permitem visualizar como variações na demanda agregada afetam o produto de equilíbrio via o princípio da demanda efetiva.

1. Parte 2 – Modelos de Demanda Agregada Esta parte compõe-se de dois capítulos (4 e 5) com distintos modelos discutindo os determinantes da demanda agregada.

2. Capítulo 4 Modelos simplificados de determinação da renda

3. Aula Anterior CAPÍTULO 3 – Visão geral da evolução da macroeconomia 3.1 A macroeconomia antes da Teoria Geral; 3.2 A Teoria Geral do Emprego, do Juro e da Moeda; 3.3 Da Teoria Keynesiana à Síntese Neoclássica; 3.4 Os Monetaristas; 3.5 Os Novos Clássicos e os Novos-Keynesianos; 3.6 Os Pós-Keynesianos; 3.7 A Teoria do Desequilíbrio; 3.8 A Nova Teoria do Crescimento; 3.9 Os Modelos que serão desenvolvidos.

4. Nesta Aula CAPÍTULO 4 – Modelos macroeconômicos simplificados de determinação de renda 4.1 A identidade dispêndio-renda; 4.2 A identidade dispêndio renda em valores reais; 4.3 A distinção entre investimento planejado e realizado; 4.4 1º Modelo macroeconômico simplificado; 4.5 2º Modelo macroeconômico simplificado; 4.6 Limitações dos modelos macroeconômicos discutidos até agora.

5. Introdução A macroeconomia atém-se a duas questões principais: 1 a ) O que determina o nível de produto efetivo em relação ao produto potencial em um dado período de tempo? Este é o problema da determinação da renda. 2 a ) O que determina o nível e a taxa de crescimento do produto de pleno emprego ou produto potencial? Esta é a questão básica da Teoria do Crescimento. Este curso se atém ao problema da determinação da renda, ou seja, à primeira questão supramencionada.

6. A origem dos modelos simplificados Paul Samuelson propôs um modelo macroeconômico simplificado (de fácil visualização gráfica) que explicasse a determinação do nível de produto de equilíbrio e que evidenciasse o princípio da demanda efetiva. Há diversas versões do modelo simplificado e o curso apresenta duas dessas versões.

7. Hipóteses dos modelos simplificados (1) consideram apenas um dos mercados em que a macroeconomia divide a economia, que é o mercado de bens e serviços; (2) o nível de preço é considerado como sendo constante; (3) o investimento privado é determinado fora do modelo (ou seja, o investimento privado é exógeno ao modelo); (4) não consideram a presença de moeda em sua análise.

8. Utilidades dos modelos simplificados Os modelos simplificados permitem: a demonstração do princípio da demanda efetiva, ou seja, são variações da demanda agregada que afetam o nível de produto (ou renda) e não o inverso; visualizar e quantificar o efeito multiplicador de um aumento de gastos autônomos sobre o produto de equilíbrio;

9. Utilidades dos modelos simplificados Os modelos simplificados permitem: analisar os efeitos, sobre o produto de equilíbrio, de um aumento de gastos do governo de mesma magnitude que o aumento de arrecadação de impostos; analisar os efeitos sobre o produto de equilíbrio do aumento de propensão marginal a poupar sobre a renda disponível.

10. A identidade entre dispêndio e renda Supondo Rf = 0, tem-se: Y = C + Ir + G + (X – M) ótica do dispêndio Y = C + S + T ótica da alocação da renda gerada Assim: C + Ir + G + (X – M)  Y  C + S + T Dispêndio Renda

11. A identidade entre dispêndio e renda em valores reais Devido a inflação, o valor real é diferente do valor nominal. Tem-se, por exemplo, y = Y/P. Assim, em termos reais surgem: Ou, subtraindo c em ambos os membros

12. A identidade entre dispêndio e renda em valores reais Produto final, em bens e serviços, não consumido pelas famílias Parcela da renda que não é consumida = poupança social

13. Determinantes do investimento privado Reagrupando as variáveis, tem-se: Observe que o investimento privado tem que ser igual à soma da poupança privada, do superávit do governo (t – g) e do déficit em transações correntes (m – x).

14. Investimento planejado versus investimento realizado Tem-se que: ir = ip + in ir = investimento realizado ip = investimento planejado. (Investimento desejado pelas firmas no início do processo de produção) in = investimento não-planejado mas realizado. (Investimento que ocorre no final do período) Por definição, tem-se: ip = FBKF + VPE ir = FBKF + VPE + VNPE VPE = variação planejada em estoques VNPE = variação não planejada em estoques

15. Investimento planejado versus investimento realizado No início do processo de produção: c + ip + g + (x – m) = y = c + s +t ( ex-ante ou planejada) No final do processo de produção: c + ir + g + (x – m)  y  c + s +t ( ex-post ou realizada) Se ip = ir, obtém-se a renda de equilíbrio, y e , igual ao PIB de equilíbrio: c + ip + g + (x – m) = y e = c + s +t Demanda Agregada (y d ) Produto Agregado (y o )

16. Investimento planejado versus investimento realizado No início do processo de produção: c + ip + g + (x – m) = y = c + s +t ( ex-ante ou planejada) No final do processo de produção: c + ir + g + (x – m)  y  c + s +t ( ex-post ou realizada) Se ip = ir, obtém-se a renda de equilíbrio, y e , igual ao PIB de equilíbrio: c + ip + g + (x – m) = y e = c + s +t Subtraindo c em todos os membros: ip + g + (x – m) = y e – c = s +t

17. Primeiro modelo macroeconômico simplificado Supõe-se, inicialmente, que ip, g, t, x e m são dados à economia. O consumo depende da renda disponível, isto é: c = f (y – t) Supondo que a função consumo seja linear: c = a 0 + a 1 ·(y – t) a 0 = consumo mínimo da coletividade. Mesmo que ( y – t) = 0, a sociedade tem que consumir um mínimo para sobreviver. a 1 = propensão marginal a consumir (PMgC)

18. Primeiro modelo macroeconômico simplificado A PMgC é o acréscimo no consumo para cada unidade de acréscimo na renda disponível:

19. Primeiro modelo macroeconômico simplificado A poupança no setor privado (s) é a parcela da renda disponível não consumida: s = (y – t) – c s = (y – t) – a 0 – a 1 ·(y – t) s = – a 0 + (1 – a 1 )·(y – t) em que: (1 – a 1 ) = propensão marginal a poupar (PMgS). – a 0 = montante da dívida do setor privado no nível de renda disponível zero para garantir a sobrevivência das famílias.

20. Primeiro modelo macroeconômico simplificado A PMgS é o acréscimo na poupança do setor privado para cada unidade de acréscimo na renda disponível:

21. Primeiro modelo macroeconômico simplificado Nota-se que: PMgS + PMgC = 1 Logo: 0 < PMgS < 1 0 < PMgC < 1

22. Primeiro modelo macroeconômico simplificado Outros conceitos: Propensão Média a Consumir em relação à renda total (PMC*) : Propensão Média a Poupar em relação à renda total (PMS*):

23. Primeiro modelo macroeconômico simplificado Outros conceitos: Propensão Média a Consumir em relação à renda disponível (PMC): Propensão Média a Poupar em relação à renda disponível (PMS):

24. Primeiro modelo macroeconômico simplificado A PMC e a PMS varia ao longo do tempo. Para o Brasil: Nesse período, a propensão marginal a consumir foi de 0,65. Qüinqüênio PMC PMS 1990 a 1994 0,72 0,28 1995 a 1999 0,74 0,26 2000 a 2003* 0,74 0,26

25. Igualdade entre a produção e a demanda agregada Sabe-se que: y 0 = y = c + s + t Produto Agregado Renda Alocação da Renda y d = c + ip + g + x – m Demanda Agregada em Equilíbrio

26. Equações de Equilíbrio 1 ª equação de equilíbrio: y e = c + ip + g + x – m 2 ª equação de equilíbrio (alternativa): c + ip + g + x – m = c + s + t ip + g + x – m = s + t Produto não consumido pelas famílias Poupança Social

27. Equações de Equilíbrio Tomando a 1 ª equação de equilíbrio: y e = c + ip + g + x – m Considere que ip, g, x, m e t sejam dados e c = a 0 + a 1 · (y – t) (comportamento) Substituindo a função consumo na equação de renda de equilíbrio, tem-se: y e = a 0 + a 1 · (y e – t) + ip + g + x – m

28. y e = a 0 + a 1 · (y e – t) + ip + g + x – m y e = a 0 + a 1 · y e – a 1 · t + ip + g + x – m y e · (1 – a 1 ) = a 0 – a 1 · t + ip + g + x – m Equações de Equilíbrio y e = 1 · (a 0 – a 1 · t + ip + g + x – m) 1 – a 1 Equação de determinação do PIB de Equilíbrio

29. Exemplos Considere que c = 10 + 0,8 · (y – t) ip=10 g=5 t=5 x=6 m=5 y e =??? y e = 1 · (10 – 0,8 · 5 +10 + 5 + 6 – 5) 1 – 0,8 y e = 110

30. Exemplos Considere que c = 10 + 0,8 · (y – t) ip=11 g=5 t=5 x=6 m=5 y e =??? y e = 1 · (10 - 0,8 · 5 +11 + 5 + 6 – 5) 1 – 0,8 y e = 115 Δ ip = 1 Δ y e = 5

31. Igualdade produto = dispêndio 45º y d y y o = y d

32. Curva de dispêndio y d y a 0  a 1 .t + ip + g + x  m a 0  a 1 .t + ip + g a 0  a 1 .t + ip a 0  a 1 .t c + ip + g + (x  m) c + ip + g c + ip x  m g ip c = (a 0  a 1 .t) + a 1 .y

33. Determinação do produto de equilíbrio 45º y d y y o = y d a 0  a 1 .t + ip + g + x  m c+ip+g+(x  m) E in > 0 y 1 y 2 y e F G I H in < 0 A variável de ajuste é a produção e não o preço Princípio da Demanda Efetiva

34. A condição de Equilíbrio é: y 0 = y = c + s + t y d = c + ip + g + x – m 1ª Alternativa: y = c + ip + g + x – m 2ª Alternativa: ip + g + x – m = s + t Determinação do produto de equilíbrio

35. Sabe-se que: s = – a 0 + (1 – a 1 ) · (y – t) Determinação do produto de equilíbrio s + t = = – a 0 + (1 – a 1 ) · y – (1 – a 1 ) · t + t s + t = – a 0 – t + a 1 ·t + t + (1 – a 1 ) · y s + t = – a 0 + a 1 · t + (1 – a 1 ) · y Intercepto

36. Determinação do produto de equilíbrio y s + t s + t ip+g+(x  m) ip + g + (x  m) E in > 0 y 1 y 2 y e in < 0  a 0 + a 1 .t F G I H

37. Efeitos do aumento da Parcimônia sobre o nível de Renda PMgS (1 – a 1 ) a 1 (1 – a 1 ) = 0,3 a 1 = 0,7 (1 – a 1 ) = 0,4 a 1 = 0,6

38. Efeitos da parcimônia sobre a renda y s 1 + t s + t ip + g + (x  m) ip + g + (x  m) E y e s 0 + t F y f As retas s 1 + t e s 0 + t não são paralelas in > 0

39. Efeitos da parcimônia sobre a renda y s 1 + t s + t ip + g + (x  m) ip + g + (x  m) E y e s 0 + t F y f O que ocorre se ip for considerado uma função direta da renda?

40. Modelo Macroeconômico Simplificado Alternativo Equações de Comportamento: Ip = ip (y) c = c (y-t) s = s (y-t) Variáveis exógenas: g , x , m , t

41. Modelo Macroeconômico Simplificado Alternativo ( s + t) 0 ( s + t) 1 y f F s 1 + t Paradoxo da Parcimônia s 0 + t ip + g + x – m y y e s + t ip + g + (x  m) E

42. O multiplicador de Despesas Autônomas Efeitos do aumento do investimento planejado. y s + t s + t ip + g + (x  m) ip 1 + g + (x  m) E y e H y h ip 0 + g + (x  m)  ip>0 A razão é o multiplicador do investimento

43. O multiplicador de Despesas Autônomas Multiplicador = Δ y/ Δ ip

44. O multiplicador de Despesas Autônomas Multiplicador = Δ y/ Δ ip Sabe-se que 0 < PMgS < 1, portanto, o multiplicador >1

45. Etapas do Raciocínio do Multiplicador ( ··· ) Etapa Dispêndio Renda 1 ª R$ 10 milhões (investimento) 10 milhões 2 ª PMgC · 10 milhões (consumo) PMgC · 10 milhões 3 ª (PMgC) 2 · 10 milhões (consumo) (PMgC) 2 · 10 milhões 4 a (PMgC) 3 · 10 milhões (consumo) (PMgC) 3 · 10 milhões

46. Multiplicador Δ y = 10 + PMgC · 10 + PMgC 2 · 10 + PMgC 3 · 10 + + PMgC 4 10 + .... Δ y = 10 (1 + PMgC + PMgC 2 + PMgC 3 + PMgC 4 + + ...) Δ y = 10 · (PMgC 0 + PMgC 1 + PMgC 2 + PMgC 3 + + PMgC 4 + ...)

47. Multiplicador Generalizando,

48. Teorema do Orçamento Equilibrado O que ocorre se g for aumentado na mesma magnitude que t for aumentado?  g =  t = z  g tem efeito imediato sobre o nível de demanda agregada.  t tem efeito imediato sobre a renda disponível, mas apenas a parcela PMgC ·  t terá o efeito multiplicador da renda.

49. Teorema do Orçamento Equilibrado  g = z > 0 Sendo  y 1 > 0  t = z > 0 Sendo  y 2 < 0

50. Teorema do Orçamento Equilibrado Mas  g =  t = z Logo:

51. Orçamento Equilibrado O teorema do orçamento equilibrado diz que se houver aumento nos gastos do governo no mesmo valor que ocorrer aumento de tributos, haverá aumento idêntico na renda de equilíbrio. Advertência : o teorema do orçamento equilibrado só ocorre no 1º Modelo Macroeconômico Simplificado.

52. Produto de Pleno Emprego Produto de pleno emprego é o máximo produto que a economia pode gerar com alocação econômica de seus recursos disponíveis.

53. Produto de Pleno Emprego Políticas para aumentar o produto de equilíbrio: y s + t s + t ip + g + (x  m) ip + g + (x  m) E y e y p

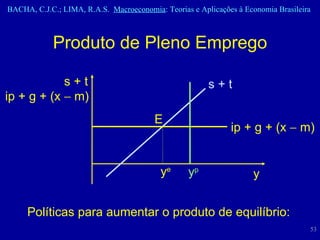
54. Produto de Pleno Emprego Para ser atingido o pleno emprego, será necessário deslocar a reta [ip + g + (x – m)] para cima e/ou a reta (s + t) para baixo e para direita. Várias medidas podem ser tomadas isoladamente ou em conjunto, tais como: ip  , g  , x  t  , m  Para tanto, o governo pode atuar sobre as políticas monetária, fiscal e cambial.

55. 1º Modelo Macroeconômico Simplificado y = c + ip + g + x – m ou ip + g + x – m = s + t Condição de equilíbrio Em que ip, g, x, m e t são valores determinados exogenamente. Sendo c = c(y – t) e s = s(y – t) Equações de comportamento

56. 1º Modelo Macroeconômico Simplificado Modelo com três equações e três variáveis endógenas (y, c e s)  tem solução matemática.

57. 2º Modelo Macroeconômico Simplificado Até agora, t = cte. Suponha t = t (y) y t t (y)

58. Função Consumo: c = c [y – t (y)] Função Poupança Privada: s = s [y – t (y)] 2º Modelo Macroeconômico Simplificado

59. 2º Modelo Macroeconômico Simplificado y = c + ip + g + x – m ou ip + g + x – m = s + t Condição de equilíbrio Em que ip, g, x, e m são valores determinados exogenamente. Sendo c = c[y – t(y)] s = s[y – t(y)] t = t(y) Equações de comportamento

60. 2º Modelo Macroeconômico Simplificado Modelo com quatro equações e quatro variáveis endógenas (y, c, s e t)  tem solução matemática.

61. Duas questões a serem respondidas: O multiplicador de gastos autônomos é idêntico ao modelo anterior? Se ele não for, ainda continua sendo maior que 1? Ainda continua válido o teorema do orçamento equilibrado? Se ele não for, o que ocorre com a renda se Δ g = Δ t? 2º Modelo Macroeconômico Simplificado

62. 2º Modelo Macroeconômico Simplificado t’ = taxa marginal de tributação Se ocorrerem funções lineares,

63. Para: 2º Modelo Macroeconômico Simplificado Tem-se:

64. Em resumo, para um aumento Δ y : Aumento do tributo: Δ t = t’ Δ y Aumento da poupança privada: Δ s = s’ (1 – t’) Δ y Aumento da poupanca social Δ (s + t) = Δ s + Δ t = s’(1 – t’) Δ y + t’ Δ y = Δ y [s’ (1 – t’) + t’] 2º Modelo Macroeconômico Simplificado

65. Δ (s + t) = Δ y [s’ (1 – t’) + t’] = Δ y [s’ – s’t’ + t’ ] = Δ y [s’ + t’ (1 – s’) ] Em resumo: Δ (s + t) = [s’ + t’ (1 – s’) ] Δ y Δ (s + t) / Δ y = s’ + t’ (1 – s’) 2º Modelo Macroeconômico Simplificado Tangente da inclinação da função poupança social no 2 o modelo

66. No 1º Modelo Macroeconômico Simplificado: O t é dado. Portanto, quando varia a renda, Δ t = 0 Δ s = s’ Δ y. O acréscimo na poupança social é igual ao da poupança privada Acréscimo da poupança social Δ (s + t) = Δ s + Δ t = s’ Δ y + 0, Portanto, Δ (s + t) = s’ Δ y , Δ (s + t) / Δ y = s’ 2º Modelo Macroeconômico Simplificado Tangente da inclinação da função poupança social no 1 o modelo

67. 2º Modelo Macroeconômico Simplificado Curvas de poupança social. y s [y  t(y)]+ t(y) s + t Δ (s + t) / Δ y = s’ Δ (s + t) / Δ y = s’ + t’ (1 – s’) s (y  t ) + t

68. O Multiplicador de Gastos Autônomos Multiplicador do investimento y s + t ip + g + (x  m) ip 0 + g + (x  m) E y 0 s[y  t(y)] + t(y) ip 1 + g + (x  m) F y 2 G y 1 s (y  t ) + t

69. O Multiplicador de Gastos Autônomos 1º MMS: Δ y/ Δ ip = 1/(1 – PMgC) = (y 1 – y 0 )/ (ip 1 – ip 0 ) 2º MMS: Δ y/ Δ ip = (y 2 – y 0 )/ (ip 1 – ip 0 ) O multiplicador do 1º MMS é maior que o multiplicador do 2º MMS.

70. Fórmula do Multiplicador de Gastos Autônomos 2º MMS: Δ y/ Δ ip = 1/ tg σ tg σ = Δ (s + t)/ Δ y = s’+ t’ (1 – s’) Multiplicador = 1 / [ s’+ t’ (1 – s’) ]

71. Multiplicador de Gastos Autônomos 1º MMS: 1/(1 – PMgC) = 1/ s’ 1 / [ s’+ t’ (1 – s’) ] < 1/ s’ Será que é maior que 1? 1 / [ s’+ t’ (1 – s’) ] > 1 Sabe-se que 0 < s’ < 1

72. Multiplicador de Gastos Autônomos 1º MMS: 1/(1 – PMgC) = 1/ s’ 1 / [ s’+ t’ (1 – s’) ] < 1/ s’ Será que é maior que 1? 1 / [ s’+ t’ (1 – s’) ] > 1 [ s’+ t’ (1 – s’) ] < 1

73. Multiplicador de Gastos Autônomos t’ (1 – s’) < 1 – s’ t’ < (1 – s’) / (1 – s’), t’ < 1 Para o multiplicador de gastos autônomos do 2º MMS ser maior que 1, é necessário: 0 < s’ <1 t’ < 1 É o que ocorre, pois não é socialmente e politicamente correto que, para cada R$ 1 a mais de renda, o governo arrecade mais de R$ 1 em tributos adicionais.

74. Multiplicador de Gastos Autônomos O multiplicador de gastos autônomos é: Δ y/ Δ ip = 1 / [ s’+ t’ (1-s’) ] Esse mesmo multiplicador continua se ao invés de aumento de investimento privado ocorrer aumento dos gastos do governo. Isto é: Δ y/ Δ g = 1 / [ s’+ t’ (1-s’) ]

75. Modificações das alíquotas de Tributos Considere variações de alíquotas de tributos (  ) e não do total de tributos (t). Inicialmente, tem-se a alíquota de  ’ 0 = 0,18 Agora, passa-se a ter  ’ 1 = 0,20 Δ  =  ’ 1 –  ’ 0 = 0,02 Δ  > 0  Δ y d = - Δ  y 0

76. Se Y 0 = 2000 t’ 0 = 0,18  y d0 = 1640 t’ 1 = 0,20  y d1 = 1600 Δ y d = - 40 Modificações das alíquotas de Tributos

77. Considere que o governo aumente a arrecadação de ( Δ  y 0 ) e automaticamente aumente seus gastos em ( Δ  y 0 ) Δ y 1 = multiplicador . (- c’ Δ  y 0 ) Δ y 1 = 1 . Modificações das alíquotas de Tributos s’+ t’ (1-s’) [- (1 – s’) Δ  y 0 ]

78. Δ y 2 = 1 . Δ g = 1 Modificações das alíquotas de Tributos s’+ t’ (1-s’) ( Δ  y 0 ) s’+ t’ (1-s’) Δ y = Δ y 1 + Δ y 2 = (- c’ Δ  y 0 ) s’+ t’ (1-s’) s’+ t’ (1-s’) + s’+ t’ (1-s’) (1- c’) Δ  y 0 ( Δ  y 0 ) Δ y = Δ y 1 + Δ y 2 =

79. Modificações das alíquotas de Tributos Como Δ y = Δ y 1 + Δ y 2 = s’+ t’ (1-s’) (1- c’) Δ  y 0 < 1 s’+ t’ (1-s’) s’ Δ y < Δ  y 0

80. Limitações dos modelos macroeconômicos já discutidos Considerou-se apenas o mercado de produto, não analisando os mercados de moeda, títulos, trabalho e divisa; Os dois modelos supõem preço sendo constante e o investimento sendo determinado fora do modelo. Além disso, os modelos discutidos não levam em conta a presença de moeda; Foi suposto que nenhuma mudança tecnológica ocorre no período de análise;

81. Limitações dos modelos macroeconômicos já discutidos O estoque físico-produtivo de fator capital também é constante. Os investimentos feitos não alteram a capacidade de produção, pois não se completam. A função consumo é muito simples. Pode-se incluir outras variáveis afetando o consumo privado (taxa de juros, expectativas de preços e de renda, distribuição de renda, entre outras).

82. Próxima Aula CAPÍTULO 5 – Modelo IS-LM para uma economia fechada 5.1 Determinação da curva de demanda agregada; 5.1.1 A curva IS – O equilíbrio no mercado de produto; 5.1.2 A curva LM – o equilíbrio no mercado moedas e títulos; 5.1.3 Equilíbrio simultâneo nos mercados de produto e de moeda; 5.1.4 A curva de demanda agregada; 5.1.5 Política fiscal e monetária.

83. Referências Bibliográficas BACHA, C.J.C.; LIMA, R.A.S. Macroeconomia : Teorias e Aplicações à Economia Brasileira. Campinas: Alínea, 2006 BLANCHARD, O. Macroeconomia : teoria e política econômica. 2 ed. Rio de Janeiro: Campus, 2001. BRANSON , W.H. e LITVACK, J.M. Macroeconomia , São Paulo: Habra, 1978. DORNBUSCH, R. & FISCHER, S. Macroeconomia . 5 a edição. São Paulo: Makron/Mcgraw-Hill, 1991. RIZZIERI, J.A.B. Teoria da determinação da renda. In: PINHO, D. Manual de economia . São Paulo: Saraiva, 1988. SAMUELSON, P. Introdução à análise econômica . Rio de Janeiro: Agir, 1968 MANKIW, N.G. Macroeconomia : Rio de Janeiro: LTC, 2004.