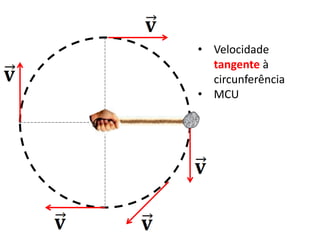
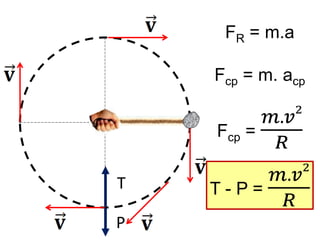
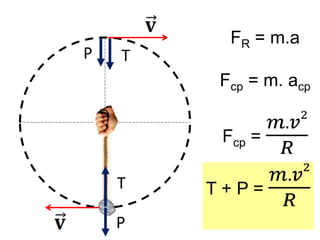
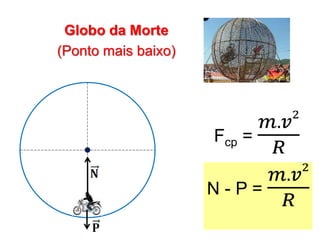
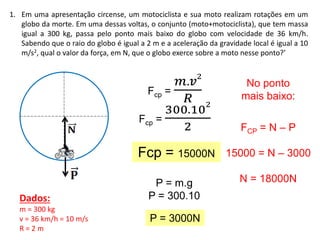
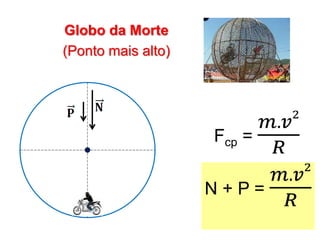
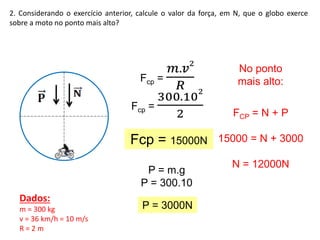
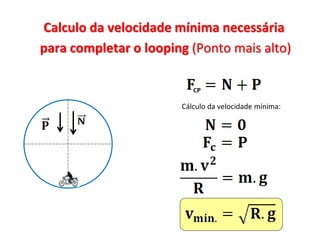
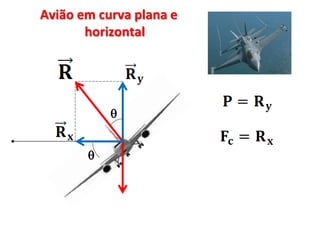
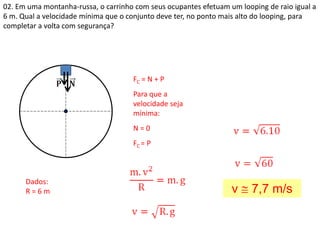
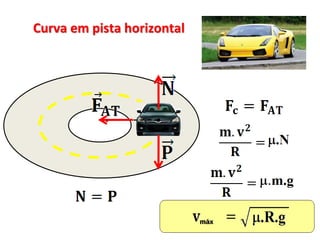
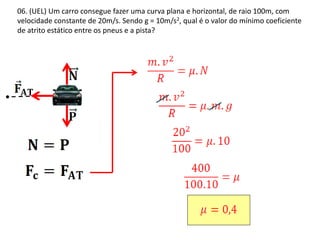
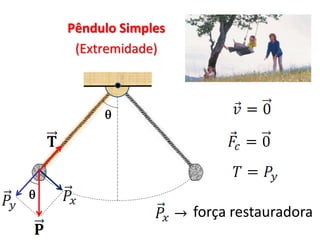
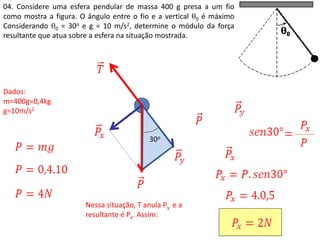
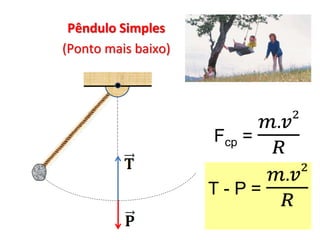
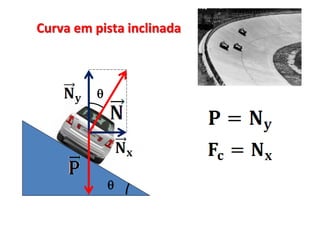
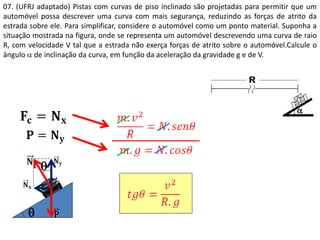
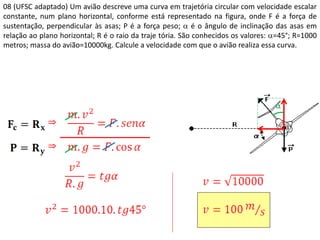
1. O documento discute conceitos de força centrípeta em situações como globo da morte, looping em montanha-russa, pêndulo simples e curvas em pistas e voo de avião. 2. São apresentados exemplos numéricos de cálculo de força centrípeta em diferentes situações como globo da morte, velocidade mínima para looping, tração em pêndulo e ângulo de inclinação em pista curva. 3. São abordados conceitos como força centrípeta, força peso, vel

1. Força Centrípeta
1
Professor Thiago

2. • Velocidade
tangente à
circunferência
• MCU

3. T
P
FR = m.a
Fcp = m. acp
Fcp =
𝑚.𝑣2
𝑅
T - P =
𝑚.𝑣2
𝑅

4. T
P
T + P =
𝑚.𝑣2
𝑅
T
FR = m.a
Fcp = m. acp
Fcp =
𝑚.𝑣
2
𝑅
P

5. 5
Quando um móvel realiza um
MCU, a resultante das forças age
em uma direção radial, ou seja,
tem a direção do raio da curva e
sentido para o centro.

6. Globo da Morte
(Ponto mais baixo)
Fcp =
𝑚.𝑣2
𝑅
N - P =
𝑚.𝑣2
𝑅

7. 1. Em uma apresentação circense, um motociclista e sua moto realizam rotações em um
globo da morte. Em uma dessas voltas, o conjunto (moto+motociclista), que tem massa
igual a 300 kg, passa pelo ponto mais baixo do globo com velocidade de 36 km/h.
Sabendo que o raio do globo é igual a 2 m e a aceleração da gravidade local é igual a 10
m/s2, qual o valor da força, em N, que o globo exerce sobre a moto nesse ponto?’
No ponto
mais baixo:
FCP = N – P
15000 = N – 3000
N = 18000N
Dados:
m = 300 kg
v = 36 km/h = 10 m/s
R = 2 m
Fcp =
𝑚.𝑣
2
𝑅
Fcp =
300.102
2
Fcp = 15000N
P = m.g
P = 300.10
P = 3000N

8. Fcp =
𝑚.𝑣2
𝑅
N + P =
𝑚.𝑣2
𝑅
Globo da Morte
(Ponto mais alto)

9. 2. Considerando o exercício anterior, calcule o valor da força, em N, que o globo exerce
sobre a moto no ponto mais alto?
No ponto
mais alto:
FCP = N + P
15000 = N + 3000
N = 12000N
Dados:
m = 300 kg
v = 36 km/h = 10 m/s
R = 2 m
Fcp =
𝑚.𝑣2
𝑅
Fcp =
300.102
2
Fcp = 15000N
P = m.g
P = 300.10
P = 3000N

10. Cálculo da velocidade mínima:
Calculo da velocidade mínima necessária
para completar o looping (Ponto mais alto)

11. 02. Em uma montanha-russa, o carrinho com seus ocupantes efetuam um looping de raio igual a
6 m. Qual a velocidade mínima que o conjunto deve ter, no ponto mais alto do looping, para
completar a volta com segurança?
Dados:
R = 6 m
FC = N + P
Para que a
velocidade seja
mínima:
N = 0
FC = P
v  7,7 m/s

12. Curva em pista horizontal

13. 06. (UEL) Um carro consegue fazer uma curva plana e horizontal, de raio 100m, com
velocidade constante de 20m/s. Sendo g = 10m/s2, qual é o valor do mínimo coeficiente
de atrito estático entre os pneus e a pista?

14. Pêndulo Simples
(Extremidade)

força restauradora


15. 04. Considere uma esfera pendular de massa 400 g presa a um fio
como mostra a figura. O ângulo entre o fio e a vertical 0 é máximo
Considerando 0 = 30o e g = 10 m/s2, determine o módulo da força
resultante que atua sobre a esfera na situação mostrada.
30o
Nessa situação, T anula Py e a
resultante é Px. Assim:
Dados:
m=400g=0,4kg
g=10m/s2
30o

16. Pêndulo Simples
(Ponto mais baixo)
Fcp =
𝑚.𝑣2
𝑅
T - P =
𝑚.𝑣2
𝑅

17. 05. (ITA) Considere um pêndulo simples de comprimento L e massa m abandonado da horizontal
num local onde a aceleração da gravidade é g. Então, para que não arrebente, o fio do pêndulo
deve ter uma resistência à certa tração. Determine o valor dessa tração em função das
grandezas dadas.

18. Curva em pista inclinada



19. 07. (UFRJ adaptado) Pistas com curvas de piso inclinado são projetadas para permitir que um
automóvel possa descrever uma curva com mais segurança, reduzindo as forças de atrito da
estrada sobre ele. Para simplificar, considere o automóvel como um ponto material. Suponha a
situação mostrada na figura, onde se representa um automóvel descrevendo uma curva de raio
R, com velocidade V tal que a estrada não exerça forças de atrito sobre o automóvel.Calcule o
ângulo  de inclinação da curva, em função da aceleração da gravidade g e de V.



20. Avião em curva plana e
horizontal



21. 08 (UFSC adaptado) Um avião descreve uma curva em trajetória circular com velocidade escalar
constante, num plano horizontal, conforme está representado na figura, onde F é a força de
sustentação, perpendicular às asas; P é a força peso;  é o ângulo de inclinação das asas em
relação ao plano horizontal; R é o raio da traje tória. São conhecidos os valores: =45°; R=1000
metros; massa do avião=10000kg. Calcule a velocidade com que o avião realiza essa curva.


