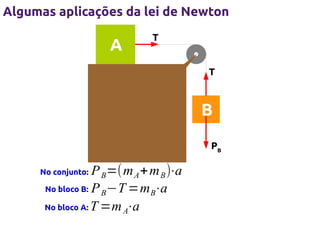
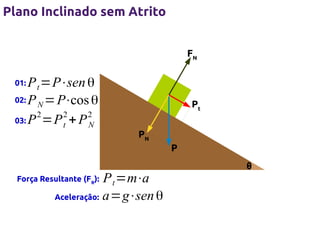
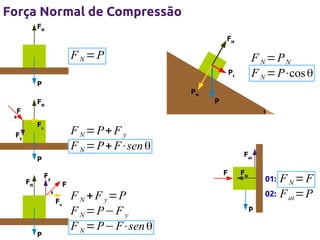
1) O documento descreve as três leis de Newton da dinâmica e suas aplicações, incluindo a força normal, peso, máquina de Atwood e plano inclinado. 2) A segunda lei de Newton estabelece que a aceleração de um corpo é diretamente proporcional à força aplicada e inversamente proporcional à sua massa. 3) Os problemas do elevador são explicados usando a segunda lei de Newton para mostrar como a força normal e a gravidade aparente mudam com a aceleração do elevador.

1. DINÂMICA

2. Leis de Newton
1ª Lei de Newton: Princípio da Inércia
“Um corpo não pode alterar seu estado de repouso ou de movimento a não ser que uma
força externa atue sobre ele” a = 0 e v = 0 → Corpo em repouso
a = 0 e v ≠ 0 → Corpo em MRU
2ª Lei de Newton: Princípio Fundamental da Dinâmica
“Um corpo submetido a uma força adquire na direção e sentido desta força uma
aceleração que é diretamente proporcional à força aplicada e inversamente proporcional
a sua massa”
a
F
A
F R =m A⋅a
3ª Lei de Newton: Princípio da Ação e Reação
“À toda força de ação corresponde uma força de reação de mesma intensidade (ou
módulo), mesma direção e sentidos opostos”
Obs: Um par de forças ação e reação não se equilibram, isto é, não se anulam pois estão
aplicadas em corpos diferentes.

3. Peso e Força Normal
Peso (P): É a força com que a Terra atrai um corpo.
FN
g
A
B
P A =m A⋅g
PA
Força Normal (FN): É a força que um plano exerce sobre o corpo (bloco). Logo, só há
força normal quando o corpo estiver sobre uma superfície.
Obs:
• A Força Normal e o Peso não podem constituir um par ação-reação, pois estão aplicadas
no mesmo corpo.
• A Força Normal só é igual ao Peso se for aplicada perpendicularmente a um plano
horizontal.

4. Algumas aplicações da lei de Newton
F
A
B
F
A
FBA FAB
Par de forças ação-reação: F BA =−F AB
No conjunto: F =(m A +m B )⋅a
No bloco A: F − F BA =m A
⋅a
No bloco B: F AB =m B⋅a
B

5. Algumas aplicações da lei de Newton
B
T
F =(m A +m B )⋅a
No bloco A: F −T =m ⋅a
A
No bloco B: T =m B⋅a
No conjunto:
T
A
F

6. Algumas aplicações da lei de Newton
A
T
T
B
PB
P B=(m A +m B )⋅a
No bloco B: P B−T =m B⋅a
No bloco A: T =m A
⋅a
No conjunto:

7. Problemas do Elevador
1º – Elevador parado ou
subindo ou descendo em MU.
FN
P
F N=P
P ap = P
gap: Gravidade aparente
Pap: Peso aparente
Pap = FN
2º – Elevador subindo em
movimento acelerado.
FN > P
v a
FN
g
P
3º – Elevador subindo em
movimento retardado.
P > FN
v a
FN
g
P
01: F N − P=m⋅a
01: P − F N =m⋅a
F N −m⋅g =m⋅a
F N =m⋅g +m⋅a
F N =m⋅( g +a)
02: g ap = g +a
m⋅g − F N =m⋅a
−F N =m⋅a−m⋅g
F N =m⋅g −m⋅a
F N =m⋅( g −a)
02: g ap = g −a

8. Problemas do Elevador
4º Elevador descendo em
movimento acelerado.
P > FN
v a
FN
g
5º Elevador descendo em
movimento retardado.
FN > P
v a
02:
F N =m⋅( g−a)
g ap = g−a
FN
g
6º – Cabo do elevador se
rompe – Queda livre (a = g) .
v a
P
P
01:
Pap = FN
01:
02:
F N =m⋅( g +a)
g ap = g +a
Dica:
Quando os sentidos da aceleração da gravidade e do elevador
forem opostos: FN > P ; gap = g + a.
Quando os sentidos da aceleração da gravidade e do elevador
forem iguais: P > FN ; gap = g - a.
FN
P
01: a ap = g −a
a ap = g − g
a ap =0
02: F N =m⋅0
F N =0
g

9. Máquina de
Atwood
2T
T
a
T
A
B
PA
PB
P A −P B =( m A +m B )⋅a
No bloco A: P A −T =m A⋅a
No bloco B: T − P B =m B⋅a
No conjunto:

10. Plano Inclinado sem Atrito
FN
P t =P⋅sen θ
02: P = P⋅cos θ
N
2
2
2
03: P =P + P
t
N
01:
Pt
PN
P
P t =m⋅a
Aceleração: a=g⋅sen θ
Força Resultante (F R):
θ

11. Força Normal de Compressão
FN
FN
F N=P
F N=PN
F N = P⋅cos θ
Pt
P
PN
FN
F
P
θ
θ
Fx
F N = P+ F y
F N = P+ F⋅sen θ
Fy
Fat
P
F
Fy
FN
F N=F
02: F at =P
01:
F
θ
Fx
P
FN
F N + F y =P
F N = P− F y
F N = P− F⋅sen θ
P

12. a
F
2T
B
A
T
a
A
F
T
B
A
PB
PA
P A −P B =( m A +m B )⋅a
P A −T =m A⋅a
T − P B =m B⋅a
A
T
F =(m A + m B )⋅a
F −T =m A⋅a
T =m B⋅a
F =m⋅a
F
T
B
F
A
FBA FAB
F BA=−F AB
F =(m A +m B )⋅a
F − F BA=m A⋅a
F AB=m B⋅a
A
T
T
B
B
PB
P B =(m A +m B )⋅a
P B −T =m B⋅a
T =m A⋅a