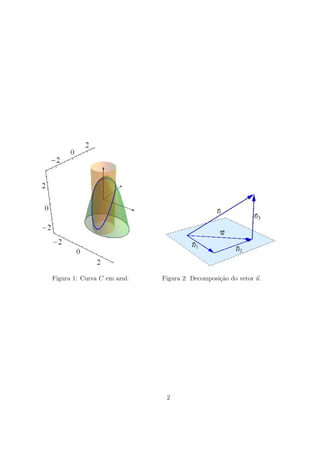
1. O documento discute a interseção de duas superfícies S1 e S2 representadas por equações, encontrando a curva C de interseção e propriedades geométricas relacionadas. 2. São solicitados o cálculo do vetor tangente u na curva C em um ponto P, a decomposição de u em componentes paralelo e normal ao plano xy, e a verificação da derivada direcional de f na direção do componente paralelo. 3. Também são solicitados o cálculo do vetor v tangente a uma reta tang

1. C´lculo III - Professor: Leandro H. Ymai - 08/02/2013
a
Exerc´
ıcio
ıcies S1 e S2 em R3 representadas pelos gr´ficos das equa¸˜es
Considere duas superf´ a co
3
z = f (x, y) = − x2 + 2y − 2y 2 , x2 + y 2 = 1,
2
respectivamente.
1- Encontre a equa¸ao vetorial R(t) da curva C de intersec¸˜o das superf´
c˜ ca ıcies (veja Figura
1.);
dR(t)
2- Encontre o vetor tangente u = dt
em algum ponto (x(t), y(t), z(t)) da curva C;
3- Decomponha o vetor u = dR(t) ˆ
= w + u3 k, onde o vetor w = u1ˆ + u2ˆ ´ a proje¸ao do
i j e c˜
dt
w
vetor u sobre o plano xy. Calcule a derivada direcional de f na dire¸ao de w =
c˜ ˆ |w|
e
u3 u3
verifique se Dw f =
ˆ |w|
em qualquer ponto (x(t), y(t), z(t)) da curva C. (Note que |w|
´o
e
coeficiente angular de um vetor em R3 , veja Figura 2)
4- Obtenha o vetor diretor v de uma reta tangente em algum ponto P (t) = (x(t), y(t), z(t))
da curva C, atrav´s do c´lculo do vetor v = N1 × N2 , onde N1 ´ o vetor normal a superf´
e a e ` ıcie
S1 em P (t) e N2 ´ o vetor normal a superf´ S2 em P (t);
e ` ıcie
5- Verifique se o vetor u ´ paralelo ao vetor v para qualquer ponto da curva C;
e
6- Encontre a equa¸˜o do plano tangente ` superf´ S1 no ponto onde ocorre o valor de
ca a ıcie
ınculo x2 + y 2 = 1;
m´ximo relativo de f , sujeito ao v´
a
7- Encontre a equa¸˜o da reta tangente ` superf´ S1 no ponto onde ocorre o valor de
ca a ıcie
m´ ınculo x2 + y 2 = 1.
ınimo relativo de f , sujeito ao v´
1

2. Figura 1: Curva C em azul. Figura 2: Decomposi¸˜o do vetor u.
ca
2