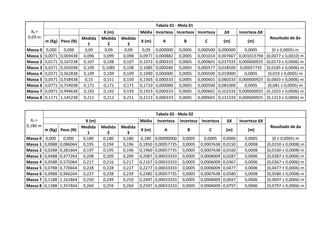
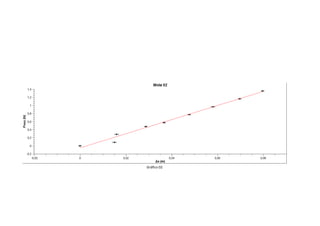
O relatório apresenta os resultados de um experimento sobre a Lei de Hooke utilizando molas. Foram medidas as deformações de duas molas ao aplicar diferentes massas e calculadas as constantes elásticas. O objetivo era comprovar a relação linear entre força e deformação prevista pela lei de Hooke para molas reais.

1. UNIVERSIDADE FEDERAL DE SERGIPE
CENTRO DE CIÊNCIAS EXATAS E TECNOLOGIA
DEPARTAMENTO DE FÍSICA
LEI DE HOOKE
Turma T5
Bruno Luis Pereira Souza
Douglas Bispo dos Santos
Juliano Almeida Perez
Antônio Roberto Leão da Cruz
Tâmara Matos dos Santos
SÃO CRISTÓVÃO
2012

2. UNIVERSIDADE FEDERAL DE SERGIPE
CENTRO DE CIÊNCIAS EXATAS E TECNOLOGIA
DEPARTAMENTO DE FÍSICA
Relatório de laboratório apresentado à
Universidade Federal de Sergipe, Centro
de Ciências Exatas e Tecnologia,
Departamento de Física, como um dos pré-
requisitos para a conclusão da disciplina
Laboratório de Física A.
Orientador: Mário Ernesto Giroldo Valerio.
SÃO CRISTÓVÃO
2012

3. 1. INTRODUÇÃO
Ao estudar molas “ideais” e suas propriedades de deformação, o cientista
inglês Robert Hooke determinou, pela primeira vez a relação existente entre a
deformação de uma mola e sua constante elástica, numa lei que recebeu seu nome,
a Lei de Hooke.
Todo material sobre o qual é exercida uma força, sofre uma deformação que
pode ou não ser observada. A lei de Hooke descreve a força restauradora que existe
nos materiais quando são deformados, comprimidos ou distendidos. Apertar ou
torcer uma borracha, esticar ou comprimir uma mola, são situações onde é fácil
notar a ocorrência da deformação. Mesmo ao pressionar uma parede com a mão,
tanto a mão como o concreto, sofrem deformações, apesar de não serem facilmente
visualizados.
A força restauradora surge sempre para recuperar o formato original do
material e vem das forças intermoleculares que mantém as moléculas e os átomos
unidos. Então, uma mola esticada ou comprimida irá retornar ao seu comprimento
original devido à ação dessa força restauradora. Quando o material volta a sua
forma original após encerrada a força que gerou a deformação, diz-se que a
deformação é pequena ou está dentro do limite elástico, pois quando as
deformações são grandes, o material ultrapassa o limite elástico e adquire uma
deformação permanente e irreversível, ou seja, ele não retorna a sua forma original.
Analiticamente a lei de Hooke é dada pela equação:
𝐹 𝑒𝑙 = −𝑘 ⋅ 𝛥𝑥
Onde "𝑘" corresponde à constante elástica da mola, uma característica inerente e
constante de cada mola. O sinal negativo indica o fato de que a força elástica tem
sentido contrário à sua deformação "𝛥𝑥". Se "𝑘" é muito grande, significa que forças
de intensidade muito grandes são necessárias para esticar ou comprimir a mola. Se
"𝑘" é pequeno, quer dizer que a força necessária para causar uma deformação é
pequena. Logo, há uma dependência linear entre "𝐹 𝑒𝑙 " e a deformação "𝛥𝑥".
Uma aplicação prática para o experimento envolvendo a Lei de Hooke, além
da comprovação da sua eficácia até certo ponto para as molas “reais”, é o da
construção de um dinamômetro. O dinamômetro de mola é um dos instrumentos que

4. se utiliza para medir forças. O mesmo é constituído de uma mola, tendo na sua
extremidade superior um cursor que desliza sobre uma escala previamente graduada
quando o dinamômetro é calibrado. Na outra extremidade da mola é aplicada uma força "𝐹"
que se quer medir conforme a Figura 01 abaixo:
Figura 01

5. 2. OBJETIVOS
 Melhorar a compreensão acerca da Lei de Hooke a partir da construção
de dinamômetros rudimentares;
 Aplicar o conceito de propagação de erros nos cálculos envolvidos para
tornar os resultados mais próximos da realidade;
 Determinar a constante elástica das molas utilizadas no experimento.

6. 3. MATERIAIS E MÉTODOS
Foram utilizados para a realização do experimento os seguintes itens:
 02 molas: Uma de metal e outra de plástico (polímero) com diâmetros
diferentes;
 Suporte para mola com tripé e escala graduada da marca Tripé Standard;
 Suporte aferido para massas;
 Conjunto de massas aferidas (10g e 50g);
 Balança analógica;
 Régua graduada de 30 cm;
 Bancada nivelada.
Segue abaixo as Figuras 02 e 03 com esboços do experimento:
Figura 02

7. Figura 03
Inicialmente, foi medida a massa do suporte para massas com o auxílio da
balança e identificado a incerteza da mesma. Em seguida, fez-se a leitura do
comprimento da mola 01 em seu estado natural, sem deformações, graduado na
escala do suporte com tripé com o auxílio de uma régua para obter a medição.
Identificou-se também a incerteza da escala graduada. Lembrando que, a cada
passo executado os valores obtidos eram anotados na tabela de dados esquemática
que será mostrada mais adiante. A distensão de uma mola é obtida com a aplicação
de uma força deformadora, neste caso, foram utilizados as massas aferidas e o
suporte para massas para fazê-la. No total, foram feitas três medições para cada
uma das oito massas distintas que foram obtidas combinando-se as massas aferidas
de 10g e 50g. O intuito de se fazer três medições, é garantir que o valor medido não
seja um erro grosseiro, caso aconteça, e tenhamos um valor médio dentro da
flutuação das medidas obtidas. Com a medição da deformação da mola para as
diversas massas em questão, obtêm-se a distensão da mola para cada caso. Depois
de feito todas as etapas anteriores e anotado todos os valores obtidos para a mola

8. 01, repetiu-se o procedimento para a mola 02, evidentemente, trocando-se apenas a
mola em questão. Após registrar todas as medidas que o experimento exige para
ambas as molas, foram sendo calculados e preenchidos os outros campos da tabela
de dados. Para efetuar esses cálculos, a tabela de dados foi projetada no Software
Microsoft Excel e então, se inseriu as fórmulas das equações nas respectivas
células, para que o programa efetuasse os cálculos.

9. 4. RESULTADOS E DISCUSSÃO
Segue abaixo as Tabelas 01 e 02 que se referem, respectivamente, às
molas 01 e 02. Estas revelam os dados obtidos com a realização do experimento e o
resultado dos cálculos envolvidos:

10. Tabela 01 - Mola 01
X0 = X (m) Média Incerteza Incerteza Incerteza ΔX incerteza ΔX
0,09 m Medida Medida Medida Resultado de Δx
m (Kg) Peso (N) X (m) A B C (m) (m)
1 2 3
Massa 0 0,000 0,000 0,09 0,09 0,09 0,09 0,000000 0,0005 0,000500 0,000000 0,0005 (0 ± 0,0005) m
Massa 1 0,0071 0,069438 0,096 0,099 0,098 0,0977 0,000882 0,0005 0,001014 0,007667 0,001013794 (0,0077 ± 0,0010) m
Massa 2 0,0171 0,167238 0,107 0,108 0,107 0,1073 0,000333 0,0005 0,000601 0,017333 0,000600925 (0,0173 ± 0,0006) m
Massa 3 0,0271 0,265038 0,109 0,1085 0,108 0,1085 0,000289 0,0005 0,000577 0,018500 0,00057735 (0,0185 ± 0,0006) m
Massa 4 0,0371 0,362838 0,109 0,109 0,109 0,1090 0,000000 0,0005 0,000500 0,019000 0,0005 (0,019 ± 0,0005) m
Massa 5 0,0571 0,558438 0,15 0,151 0,150 0,1503 0,000333 0,0005 0,000601 0,060333 0,000600925 (0,0603 ± 0,0006) m
Massa 6 0,0771 0,754038 0,171 0,171 0,171 0,1710 0,000000 0,0005 0,000500 0,081000 0,0005 (0,081 ± 0,0005) m
Massa 7 0,0971 0,949638 0,192 0,192 0,193 0,1923 0,000333 0,0005 0,000601 0,102333 0,000600925 (0,1023 ± 0,0006) m
Massa 8 0,1171 1,145238 0,211 0,212 0,211 0,2113 0,000333 0,0005 0,000601 0,121333 0,000600925 (0,1213 ± 0,0006) m
Tabela 02 - Mola 02
X0 = X (m) Média Incerteza Incerteza Incerteza ΔX Incerteza ΔX
0,180 m Medida Medida Medida Resultado de Δx
m (Kg) Peso (N) X (m) A B C (m) (m)
1 2 3
Massa 0 0,000 0,000 0,180 0,180 0,180 0,180 0,00000000 0,0005 0,0005 0,0000 0,0005 (0 ± 0,0005) m
Massa 1 0,0088 0,086064 0,195 0,194 0,196 0,1950 0,00057735 0,0005 0,0007638 0,0150 0,0008 (0,0150 ± 0,0008) m
Massa 2 0,0288 0,281664 0,197 0,195 0,196 0,1960 0,00057735 0,0005 0,0007638 0,0160 0,0008 (0,0160 ± 0,0008) m
Massa 3 0,0488 0,477264 0,208 0,209 0,209 0,2087 0,00033333 0,0005 0,0006009 0,0287 0,0006 (0,0287 ± 0,0006) m
Massa 4 0,0588 0,575064 0,217 0,216 0,217 0,2167 0,00033333 0,0005 0,0006009 0,0367 0,0006 (0,0367 ± 0,0006) m
Massa 5 0,0788 0,770664 0,228 0,228 0,227 0,2277 0,00033333 0,0005 0,0006009 0,0477 0,0006 (0,0477 ± 0,0006) m
Massa 6 0,0988 0,966264 0,237 0,238 0,239 0,2380 0,00057735 0,0005 0,0007638 0,0580 0,0008 (0,0580 ± 0,0008) m
Massa 7 0,1188 1,161864 0,250 0,249 0,250 0,2497 0,00033333 0,0005 0,0006009 0,0697 0,0006 (0,0697 ± 0,0006) m
Massa 8 0,1388 1,357464 0,260 0,259 0,260 0,2597 0,00033333 0,0005 0,0006009 0,0797 0,0006 (0,0797 ± 0,0006) m

11. Estão listadas abaixo, as equações utilizadas para calcular a média, o
desvio padrão da medida, a incerteza do tipo A, a incerteza do tipo B e a incerteza
combinada das medidas experimentais:
 MÉDIA
𝑛
− 𝑖=1 𝑥𝑖
𝑥=
𝑛
Geralmente, ao se realizar um experimento, várias medidas de um mesmo
objeto em questão são feitas para garantir um intervalo mais preciso da medição.
Por conseguinte, a média representa a melhor estimativa do valor real desejado.
 DESVIO PADRÃO DA MEDIDA
𝑛 −
𝑥𝑖 − 𝑥 2
𝑖=1
𝜎=
𝑛−1
Faz-se necessário aplicar o conceito estatístico do desvio padrão da medida,
para quantificar o grau de dispersão das medidas em relação ao valor médio.
 INCERTEZA DO TIPO A
𝜎
𝜎𝐴 =
𝑛
A incerteza do Tipo A utiliza conceitos estatísticos que se associa ao
valor médio. É estimado pelo desvio padrão da média e ainda, se torna mais exato,
quanto maior for o número de medidas envolvidas.
 INCERTEZA DO TIPO B

12. A incerteza do tipo B, ou incerteza instrumental é determinada através da
resolução do equipamento utilizado para as medições. No caso de um equipamento
digital, a incerteza de tipo B equivale à menor medida possível do aparelho; para um
equipamento analógico, deve-se dividir o menor valor da escala por dois para obter
a incerteza em questão.
 INCERTEZA COMBINADA
𝜎𝐶 = 𝜎𝐴 2 + 𝜎𝐵 2
A incerteza Combinada, representa o valor total das incertezas
associadas às medidas, ou seja, relaciona tanto a incerteza do Tipo A quanto a
do Tipo B.
Para calcular a elongação das molas, referente às diversas forças peso
pelas quais foram submetidas, foi utilizada a seguinte fórmula:
𝛥𝑥 = 𝑥 − 𝑥0
Onde o valor 𝑥0 foi medido e fixado como constante no início do experimento. Ao se
propagar a incerteza para a elongação, obtém-se:
2 2
𝜕𝛥𝑥 𝜕𝛥𝑥
𝜎 𝛥𝑥 = ⋅ 𝜎𝑥 + ⋅ 𝜎 𝑥0
𝜕𝑥 𝜕𝑥0
2
𝜎 𝛥𝑥 = 1 ⋅ 𝜎𝑥 2 + 0. 𝜎 𝑥 0
𝜎 𝛥𝑥 = 𝜎𝑥 2
𝜎 𝛥𝑥 = 𝜎 𝑥
Onde:
𝜎 𝑥 0 = 0,0005 m

13. Para o cálculo da força peso, a partir da massa determinada, utilizou-se a equação:
𝑃= 𝑚⋅ 𝑔
Onde:
𝑃 = 𝐹𝑜𝑟ç𝑎 𝑃𝑒𝑠𝑜 (𝑁);
𝑔 = 𝐴𝑐𝑒𝑙𝑒𝑟𝑎çã𝑜 𝑑𝑎 𝐺𝑟𝑎𝑣𝑖𝑑𝑎𝑑𝑒 𝑚/𝑠² .
Para calcular a propagação de incertezas da Força Peso:
2
𝜕𝑃
𝜎𝑃 = ⋅ 𝜎𝑚
𝜕𝑚
𝜎𝑃 = 𝑔⋅ 𝜎𝑚 2
𝜎𝑃 = 𝜎 𝑚 ⋅ 𝑔
Assumiu-se que a aceleração seja constante e de módulo igual a 9,78 m/s².

14. Gráfico 01

15. Gráfico 02

16. Os gráficos apresentados acima, Gráficos 01 e 02, se comportam como uma
reta, conforme expressa a equação da Lei de Hooke. Podemos afirmar que as molas
utilizadas no experimento obedecem à Lei de Hooke, porque não sofreram
deformações permanentes. Dessa forma, fica evidente que o caráter restaurador da
força exercida pela mola, Força Elástica, se manteve, fato este que caracteriza a Lei
de Hooke.
Considerando-se o módulo da Força Elástica prevista pela Lei de Hooke:
|𝐹 𝑒𝑙 | = 𝑘 ⋅ 𝛥𝑥
Podemos compará-la com a equação genérica do 1º grau que possui a seguinte
estrutura:
y = 𝑚. 𝑥 + 𝑛
Onde “n” representa um valor constante, “x” a variável e “m” o coeficiente angular.
Através da comparação de ambas as equações, podemos notar que “k” corresponde
ao valor de “m”.
O coeficiente angular de uma reta, “m”, em geral é calculado pela seguinte
maneira: Escolhem-se dois pontos distintos na reta, P1 e P2, os quais são da forma:
𝑃1 = 𝑣𝑎𝑙𝑜𝑟 𝑞𝑢𝑎𝑙𝑞𝑢𝑒𝑟 𝑒𝑚 𝑥 ; 𝑣𝑎𝑙𝑜𝑟 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑒𝑛𝑡𝑒 𝑒𝑚 𝑦
𝑃2 = 𝑣𝑎𝑙𝑜𝑟 𝑞𝑢𝑎𝑙𝑞𝑢𝑒𝑟 𝑒𝑚 𝑥 ; 𝑣𝑎𝑙𝑜𝑟 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑒𝑛𝑡𝑒 𝑒𝑚 𝑦
Em seguida, substituem-se os valores na equação abaixo e obtêm-se o resultado
realizando os devidos calculos:
y2 − y1) = m(x2 − x1
Com os dados extraídos das respectivas tabelas e utilizando o Software
SciDavis, foram calculados os respectivos coeficientes angulares de cada reta
ajustada, a seguir:

17. Para a Mola 01, o valor do coeficiente angular é de (8,867 ± 0,004);
Para a Mola 02, o valor do coeficiente angular é de (17,475 ± 0,006).
Então, para a Mola 01, k = (8,867 ± 0,004) N/m e para a Mola 02, k=(17,475 ± 0,006)
N/m.
A diferença entre os valores obtidos para a constante elástica “k” de cada
mola reflete a respectiva rigidez, resistência à deformação, de cada mola, ou seja,
quanto maior for o valor de k, mais difícil será deformá-la.
Duas dificuldades foram encontradas durante a realização do experimento,
manter estático o sistema analisado e fazer a leitura das medições. Por conseguinte,
as medidas obtidas provavelmente contém erros.

18. 5. CONCLUSÕES
Diante do exposto, é evidente que as molas utilizadas no experimento obedecem à
Lei de Hooke, pois, quando distorcidas com pesos diferentes, elas assumem elongações
diferentes. Toda mola tem seu valor próprio de constante elástica, sendo esta uma
característica inerente sua, que pode ser obtida sem muita dificuldade através do
experimento realizado. Para a validade desta lei, a força exercida sobre mola não deve
assumir valores que causem elongação superior ao limite elástico, para que não ocorra uma
deformação permanente.

19. 6. BIBLIOGRAFIA
 Deizilene e Francisco Felipe, Lei de Hooke (Força Elástica), disponível em:
http://www.fisicadescomplicada.com.br/2010/08/lei-de-hooke-forca-elastica.html,
acesso em 27/03/2012.
 Flávio Iassuo Takakura, Aula 06 - Lei de Hooke, Força Elástica, disponível em:
http://www.fisica.ufjf.br/~takakura/lab-fis1/aula6.pdf, acesso em 27/03/2012.
 HALLIDAY, David; RESNICK, Robert; WALKER, Jearl, Fundamentos de Física 1 -
Mecânica, 8ª Edição, Rio de Janeiro: Editora LTC, 2008.
 YOUNG H. D.,FREEDMAN R. A., SEARS F. W., ZEMANSKY M. W., Física,
vol. 1, ed. São Paulo, 2005.