Cálculo I engenharias

C´alculo I 1
Limites e Continuidade
Ricardo Pereira
Departamento de Matem´atica
Universidade de Aveiro
Setembro de 2012

Vizinhan¸ca 2
Def 1.1
Sejam a ∈ R e ε ∈ R+.
Chamamos vizinhan¸ca-ε de a ou vizinhan¸ca de centro a e raio ε
ao conjunto
Vε(a) := {x ∈ R: |x − a| < ε} =]a − ε, a + ε[
Exe 1.2
Determine os conjuntos:
(a) V2(3)
(b) V1
3
(−2)

Ponto interior, exterior e fronteiro 3
Def 1.3
Sejam a ∈ R e S ⊂ R.
a é ponto interior de S se existe ε > 0 tal que Vε(a) ⊂ S
a é ponto exterior de S se a é ponto interior do
complementar de S em R
a é ponto fronteiro de S se a não é ponto interior nem ponto
exterior de S
Obs 1.4
O complementar de S em R é o conjunto R S

Interior, exterior, fronteira e fecho 4
Def 1.5
Interior de S: int(S) conjunto dos pontos interiores de S
Exterior de S: ext(S) conjunto dos pontos exteriores de S
Fronteira de S: frt(S) conjunto dos pontos fronteiros de S
Fecho de S ¯S = int(S) ∪ frt(S)
Exe 1.6
Indique int(S), ext(S), frt(S) e ¯S, sendo:
(a) S = [1, 4[ ∪ {2π, 10}
(b) S = [−1, 1] ∪ {3}

Conjunto aberto, fechado e compacto 5
Def 1.7
S é um conjunto aberto se int(S) = S
S é um conjunto fechado se ¯S = S
S é um conjunto compacto se S é fechado e limitado
Obs 1.8
S ⊂ R é limitado se existe L > 0 tal que |x| ≤ L, ∀x ∈ S
Exe 1.9
Verifique se S é fechado, aberto e/ou compacto, sendo:
(a) S = [1, 4[ ∪ {2π, 10} (b) S = [−1, 1] ∪ {3}
Obs 1.10
R é aberto e fechado; R não é compacto

Ponto de acumula¸cão e ponto isolado 6
Def 1.11
a ∈ R é um ponto de acumula¸cão de S ⊂ R se toda a
vizinhan¸ca de a contém um ponto de S distinto de a, isto é,
se,
∀ε > 0, (Vε(a) {a}) ∩ S = ∅
a ∈ S é um ponto isolado de S se não é ponto de
acumula¸cão de S.
Exe 1.12
Indique os pontos de acumula¸cão e os pontos isolados de:
(a) S = [1, 4[ ∪ {2π, 10}
(b) S = 1
n : n ∈ N

Fun¸cão real de variável real 7
Def 1.13
Uma fun¸cão real de variável real f é uma correspondência que a
cada elemento de Df ⊂ R (dom´ınio de f ) faz corresponder um e
um só elemento de R. Nota¸cão: f : Df → R
Obs 1.14
1 As fun¸cões que consideraremos terão sempre dom´ınio em R.
Assim, os dom´ınios para elas considerados deverão ser sempre
tomados como subconjuntos de R, mesmo que tal esteja
omisso.
2 Os alunos devem recapitular, de forma autónoma, as várias
defini¸cões básicas relativas a f.r.v.r., tais como dom´ınio,
contradom´ınio, injetividade, sobrejetividade, monotonia, etc.
Recomenda-se a leitura atenta do texto“Pré-requisitos”e dos
apontamentos da Prof. Virg´ınia Santos, pp. 14-24, ambos
dispon´ıveis no Moodle@UA.

Limite segundo Cauchy 8
Def 1.15
Seja f : Df → R uma f. r. v. r.. Sejam a um ponto de acumula¸cão
de Df e ∈ R. Dizemos que é o limite de f no ponto a ou que
f (x) tende para quando x tende para a e escrevemos
lim
x→a
f (x) =
se,
∀ε > 0 ∃δ > 0 ∀x ∈ Df , 0 <| x − a |< δ ⇒| f (x) − |< ε
Caso a seja um ponto isolado de Df , por defini¸cão, lim
x→a
f (x)=f (a)
Obs 1.16
Esta defini¸cão traduz que f (x) está tão próximo de quanto se
queira desde que x, distinto de a, esteja suficientemente próximo
de a.

Limite segundo Heine 9
Def 1.17
Sendo a um ponto de acumula¸cão de Df , diz-se que
lim
x→a
f (x) = se para toda a sucessão (xn)n∈N de elementos de Df
convergente para a, a correspondente sucessão das imagens
f (xn)n∈N converge para .
Caso a seja um ponto isolado de Df , por defini¸cão, lim
x→a
f (x)=f (a)
Obs 1.18
As defini¸cões de limite de uma fun¸cão num ponto segundo Cauchy
e segundo Heine são equivalentes
Prop 1.19
Sejam f : Df −→ R uma fun¸cão e a ∈ R um ponto de acumula¸cão
de Df . Se existe lim
x→a
f (x), esse limite é único.

Propriedades dos limites 10
Prop 1.20
Sejam f : Df −→ R uma fun¸cão, a ∈ R um ponto de acumula¸cão
de Df e ∈ R. Então, lim
x→a
f (x) = sse lim
x→a
(f (x) − ) = 0
Prop 1.21
Sejam f e g f.r.v.r. e a um ponto de acumula¸cão de D = Df ∩ Dg .
Se lim
x→a
f (x) = 1 ∈ R e lim
x→a
g(x) = 2 ∈ R, então
1 lim
x→a
(f (x) ± g(x)) = 1 ± 2
2 lim
x→a
(αf (x)) = α 1, para todo o α ∈ R
3 lim
x→a
(f (x).g(x)) = 1 2
4 Se 2 = 0 então lim
x→a
f (x)
g(x)
=
1
2

Lei do enquadramento 11
Prop 1.22
Sejam f , g e h f.r.v.r. e a um ponto de acumula¸c˜ao de
D = Df ∩ Dg ∩ Dh. Se existir δ > 0 tal que
f (x) ≤ g(x) ≤ h(x) , para todo o x ∈ (Vδ(a) {a}) ∩ D ,
e lim
x→a
f (x) = lim
x→a
h(x) = ent˜ao lim
x→a
g(x) = .
Exe 1.23
Sabendo que, ∀x ∈ R {0}, −|x| ≤ x sen 1
x ≤ |x|, calcule
lim
x→0
sen 1
x
1
x

Produto de infinitésimo por fun¸cão limitada 12
Prop 1.24
Sejam f : Df → R, g : Dg → R e a um ponto de acumula¸cão de
Df ∩ Dg . Se
lim
x→a
f (x) = 0 e g é limitada em(Vδ(a) {a}) ∩ Dg ,
para algum δ > 0 , então
lim
x→a
f (x)g(x) = 0.
Exe 1.25
Calcule lim
x→0
x cos
1
x

Pontos de acumula¸cão laterais 13
Def 1.26
Sejam S = ∅, S ⊂ R e a ∈ R.
a é ponto de acumula¸cão à esquerda de S se
]a − δ, a[∩S = ∅, qualquer que seja δ > 0 .
a é ponto de acumula¸cão à direita de S se
]a, a + δ[∩S = ∅, qualquer que seja δ > 0 .
Exe 1.27
Considere o conjunto
S = [1, 4[ ∪ {2π, 10}
Indique os pontos de acumula¸cão à esquerda e os pontos de
acumula¸cão à direita de S

Limites laterais 14
Def 1.28
Sejam f uma f.r.v.r., a um ponto de acumula¸cão à esquerda de Df
e ∈ R. Dizemos que é o limite de f (x) quando x tende para
a por valores inferiores a a e escrevemos
lim
x→a−
f (x) =
se ∀ε > 0 ∃δ > 0 ∀x ∈ Df , a − δ < x < a ⇒| f (x) − |< ε.
Def 1.29
Sejam f uma f.r.v.r., a um ponto de acumula¸cão à direita de Df e
∈ R. Dizemos que é o limite de f (x) quando x tende para a
por valores superiores a a e escrevemos
lim
x→a+
f (x) =
se ∀ε > 0 ∃δ > 0 ∀x ∈ Df , a < x < a + δ ⇒| f (x) − |< ε.

Existência de limite 15
Prop 1.30
Sejam f uma f.r.v.r., a um ponto de acumula¸cão à direita de Df e
à esquerda de Df e ∈ R. Então
lim
x→a
f (x) = sse lim
x→a−
f (x) = = lim
x→a+
f (x).
Exe 1.31
Calcule, caso exista, lim
x→1
f (x), onde:
(a) f (x) =
x2 − 2x + 1 se x ≥ 1
1
x+1 se x < 1
(b) f (x) =



x se x < 1
3 se x = 1
1
2x−1 se x > 1

Limites finitos no infinito 16
Def 1.32
Sejam f : Df ⊂ R −→ R, Df tal que ]a, +∞[⊂ Df e ∈ R
lim
x→+∞
f (x) = se
∀ε > 0 ∃M > 0 ∀x ∈ Df , x > M ⇒| f (x) − |< ε
Sejam f : Df ⊂ R −→ R, Df tal que ] − ∞, a[⊂ Df e ∈ R
lim
x→−∞
f (x) = se
∀ε > 0 ∃M > 0 ∀x ∈ Df , x < −M ⇒| f (x) − |< ε
Obs 1.33
1 Estes limites, quando existem, são únicos.
2 As propriedades operatórias são análogas às do slide 10

Limites laterais infinitos 17
Def 1.34
Sejam f :Df ⊆R−→R e a um ponto de acumula¸cão à direita de Df
lim
x→a+
f (x) = +∞ se
∀L > 0 ∃δ > 0 ∀x ∈ Df , a < x < a + δ ⇒ f (x) > L
lim
x→a+
f (x) = −∞ se
∀L > 0 ∃δ > 0 ∀x ∈ Df , a < x < a + δ ⇒ f (x) < −L
Exe 1.35
Escreva as defini¸cões de
lim
x→a−
f (x) = +∞ e lim
x→a−
f (x) = −∞

Limites infinitos 18
Def 1.36
Sejam f : Df ⊆ R −→ R e a um ponto de acumula¸cão de Df .
lim
x→a
f (x) = +∞ se
∀L > 0 ∃δ > 0 ∀x ∈ Df , 0 <| x − a |< δ ⇒ f (x) > L
lim
x→a
f (x) = −∞ se
∀L > 0 ∃δ > 0 ∀x ∈ Df , 0 <| x − a |< δ ⇒ f (x) < −L
Obs 1.37
Também neste caso
lim
x→a
f (x) = +∞ sse lim
x→a−
f (x) = +∞ = lim
x→a+
f (x)
lim
x→a
f (x) = −∞ sse lim
x→a−
f (x) = −∞ = lim
x→a+
f (x)

Limites infinitos no infinito 19
Def 1.38
Sejam f : Df ⊆ R −→ R, Df tal que ]a, +∞[⊂ Df ,
lim
x→+∞
f (x) = +∞ se
∀L > 0 ∃M > 0 ∀x ∈ Df , x > M ⇒ f (x) > L
Sejam f : Df ⊆ R −→ R, Df tal que ] − ∞, a[⊂ Df ,
lim
x→−∞
f (x) = +∞ se
∀L > 0 ∃M > 0 ∀x ∈ Df , x < −M ⇒ f (x) > L
Exe 1.39
Escreva as defini¸cões de
lim
x→+∞
f (x) = −∞ e lim
x→−∞
f (x) = −∞

Conven¸cões: opera¸cões envolvendo −∞ e +∞ 20
Obs 1.40
(+∞) + (+∞) = +∞ e (−∞) + (−∞) = −∞
∀α ∈ R, +∞ + α = +∞ e −∞ + α = −∞
(+∞) × (+∞) = +∞, (−∞) × (−∞) = +∞ e
(+∞) × (−∞) = −∞ = (−∞) × (+∞)
∀α > 0, α × (+∞) = +∞ e α × (−∞) = −∞
∀α < 0, α × (+∞) = −∞ e α × (−∞) = +∞
0+∞ = 0 e 0−∞ = +∞
Indetermina¸cões:
0 × ∞
∞
∞
+ ∞ − ∞ 00 0
0
1∞
∞0

Conven¸cões: 0+
e 0−
21
Obs 1.41
Caso f : Df ⊂ R −→ R seja tal que lim
x→a
f (x) = 0 e que, para
algum δ > 0, f (x) > 0 [resp.f (x) < 0], para todo o
x ∈ (Vδ(a) {a}) ∩ Df , escrevemos lim
x→a
f (x) = 0+
[resp. lim
x→a
f (x) = 0−
].
Prop 1.42
1 Se lim
x→a
f (x) = ±∞, então lim
x→a
1
f (x)
= 0;
2 Se lim
x→a
f (x) = 0+
, então lim
x→a
1
f (x)
= +∞;
3 Se lim
x→a
f (x) = 0−
, então lim
x→a
1
f (x)
= −∞.

Exerc´ıcios de limites 22
Exe 1.43
Calcule, caso existam, os limites seguintes:
(a) lim
x→+∞
1
x2 − 1
(b) lim
x→+∞
3x2 + 2x − 1
5x2 − x
(c) lim
x→−∞
x − 1
x3 − 2x − 1
(d) lim
x→−∞
x2 + 1
1 − x
(e) lim
x→1+
1
x2 − 1
(f) lim
x→−1
1
x2 − 1
(g) lim
x→1
√
x − 1
x − 1
(h) lim
x→2
x4 − 16
x − 2

Fun¸cão Cont´ınua 23
Def 1.44
Sejam f : Df −→ R, a ∈ Df e ∅ = S ⊂ Df um conjunto aberto.
Dizemos que f é cont´ınua em a se o limite lim
x→a
f (x) existe e
é finito e lim
x→a
f (x) = f (a).
Caso contrário, dizemos que f é descont´ınua em a.
f é cont´ınua em S se f é cont´ınua em todo o ponto de S
Exe 1.45
Seja a ∈ R e
f (x) =



x + a2 + 6 se x < 3
9 − a se x = 3
3x + a se x > 3
Para que valores de a
(a) existe lim
x→3
f (x)
(b) f é cont´ınua em x = 3

Continuidade à direita e à esquerda 24
Obs 1.46
1 Se S = [a, b] podemos falar em continuidade lateral:
se lim
x→a+
f (x)=f (a) diz-se que f é cont´ınua à direita em a
se lim
x→b−
f (x)=f (b) diz-se que f é cont´ınua à esquerda em b
2 Se S = [a, +∞[ (resp. S =] − ∞, a]) podemos falar de conti-
nuidade à direita em a (resp. continuidade à esquerda em a)
3 Sendo S um intervalo, dizemos que f é cont´ınua em S se f é
cont´ınua no interior de S e cont´ınua lateralmente nos
extremos de S que pertencem a S.
Exe 1.47
Estude a continuidade em x = 0 da fun¸cão
f (x) =
x + 2 se x ≥ 0
−x + 1 se x < 0

Propriedades de fun¸cões cont´ınuas 25
Prop 1.48
Sejam f e g duas fun¸cões cont´ınuas num ponto a.
Então as fun¸cões f + g, αf (α ∈ R) e fg são cont´ınuas em a.
Se g(a) = 0, então f /g é também uma fun¸cão cont´ınua em a.
Prop 1.49
Sejam f :Df −→ R e g :Dg −→ R tais que a fun¸cão composta
g ◦ f está definida.
Se f é cont´ınua em a e g é cont´ınua em f (a), então g ◦ f é
cont´ınua em a.

Teorema de Bolzano 26
Teo 1.50
Seja f : [a, b] → R uma fun¸cão. Se f é cont´ınua em [a, b] e
f (a) = f (b), então,
para todo o y entre f (a) e f (b), existe c ∈]a, b[ tal que f (c) = y.
Cor 1.51
Seja f : [a, b] −→ R uma fun¸cão cont´ınua.
Se f (a) · f (b) < 0, então existe c ∈]a, b[ tal que f (c) = 0.
Exe 1.52
1 Considere a fun¸cão f (x) = x2 + 2x. Mostre, usando o
Teorema de Bolzano, que existe c ∈ ]0, 3[ tal que f (c) = 5.
2 Mostre que, no intervalo ] − 1, 0[, a fun¸cão f definida por
f (x) = −2 + 3x2 tem pelo menos um zero.

Teorema de Weierstrass 27
Teo 1.53
Se f : Df −→ R é uma fun¸cão cont´ınua e Df é um conjunto
compacto de R, então f atinge em Df o máximo e o m´ınimo
globais (isto é, existem x1, x2 ∈ Df tais que
f (x1) ≤ f (x) ≤ f (x2), ∀x ∈ Df ).
Obs 1.54
Notar que um intervalo [a, b], com a < b, é um conjunto compacto
de R. Assim, toda a fun¸cão cont´ınua em [a, b] tem a´ı máximo e
m´ınimo globais.
Exe 1.55
Seja f (x) =
x + 2 se x ≥ 0
−x + 1 se x < 0
(a) A fun¸cão f tem m´ınimo global em [−1, 1] ?
(b) A al´ınea (a) contradiz o teorema de Weierstrass?

C´alculo I 28
Derivadas
Ricardo Pereira
Setembro de 2012

Derivada num ponto 29
Def 2.1
Sejam f : Df −→ R uma fun¸cão e a ∈ Df um ponto interior de Df .
Chama-se derivada da fun¸cão f no ponto a, e denota-se por
f (a) ou df
dx (a), ao limite
lim
h→0
f (a + h) − f (a)
h
se este limite existir, podendo ser finito, +∞ ou −∞.
Neste caso, f diz-se derivável em a.
Se o limite for finito dizemos que f é diferenciável em a.
Obs 2.2
Recordar que lim
h→0
f (a + h) − f (a)
h
= lim
x→a
f (x) − f (a)
x − a
Exe 2.3
Seja f (x) = x2 + 1. Calcular, por defini¸cão, f (3).

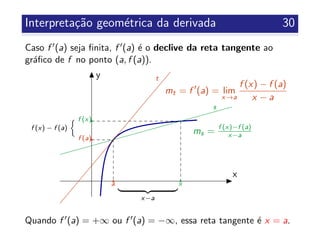
Interpreta¸cão geométrica da derivada 30
Caso f (a) seja finita, f (a) é o declive da reta tangente ao
gráfico de f no ponto (a, f (a)).
x
y
x−a
f (x) − f (a)
mt = f (a) = lim
x→a
f (x) − f (a)
x − a
ms = f (x)−f (a)
x−a
a x
f (x)
f (a)
s
t
Quando f (a) = +∞ ou f (a) = −∞, essa reta tangente é x = a.

Reta tangente e reta normal 31
Def 2.4
A equa¸cão da reta tangente à curva y = f (x) no ponto
(a, f (a)) é
y − f (a) = f (a)(x − a)
Chamamos normal à curva y = f (x) no ponto (a, f (a)) à
reta que passa nesse ponto e é perpendicular à tangente à
curva nesse ponto.
Exe 2.5
Determine a equa¸cão da reta tangente e da normal
à curva y = x2 + 1:
(a) no ponto (3, 10)
(b) no ponto (0, 1)

Derivadas Laterais 32
Def 2.6
Seja a ∈ Df um ponto de acumula¸cão à esquerda de Df .
Chama-se derivada lateral de f à esquerda de a, e
denota-se por f−(a), ao limite
lim
h→0−
f (a + h) − f (a)
h
Seja a ∈ Df um ponto de acumula¸cão à direita de Df .
Chama-se derivada lateral de f à direita de a, e denota-se
por f+(a), ao limite
lim
h→0+
f (a + h) − f (a)
h

Diferenciabilidade 33
Prop 2.7
Sejam f : Df ⊂ R → R uma fun¸cão e a ∈ Df um ponto interior de
Df . Então f é diferenciável em a sse f−(a) e f+(a) existem, são
finitas e f−(a) = f+(a).
Exe 2.8
Considere a fun¸cão f definida por
f (x) =
x2 + x4 se x ≥ 0
x3 se x < 0
(a) f é diferenciável em x = 0?
(b) Qual o valor de f (0)?

Continuidade e diferenciabilidade 34
Prop 2.9
Sejam f : Df ⊂R→R uma fun¸cão e a∈Df um ponto interior de Df
Se f é diferenciável em a, então f é cont´ınua em a.
Cor 2.10
Se f não é cont´ınua em a, então f não é diferenciável em a.
Exe 2.11
Verifique se as seguintes fun¸cões são diferenciáveis no ponto x = 0.
(a) f (x) =
sen 1
x se x = 0
0 se x = 0
(b) g(x) =
x se x ≥ 0
−x se x < 0

Regras de deriva¸cão 35
Prop 2.12
Sejam f e g duas fun¸cões diferenciáveis em a. Então
f + g é diferenciável em a e
(f + g) (a) = f (a) + g (a)
f − g é diferenciável em a e
(f − g) (a) = f (a) − g (a)
f · g é diferenciável em a e
(f · g) (a) = f (a)g(a) + f (a)g (a)
αf , com α ∈ R, é diferenciável em a e
(αf ) (a) = αf (a)

Regras de deriva¸cão 36
Prop 2.12 (cont.)
se g(a) = 0, então f
g é diferenciável em a e
f
g
(a) =
f (a)g(a) − f (a)g (a)
(g(a))2
Prop 2.13
Regra da Cadeia: Sejam f : Df → R e g : Dg → R duas fun¸cões
tais que g ◦ f está definida.
Se f é diferenciável em a e g é diferenciável em f (a), então g ◦ f é
diferenciável em a e
(g ◦ f ) (a) = g (f (a)) · f (a)

Formul´ario de derivadas 37
Obs 2.14
Sejam u e v fun¸c˜oes de x, k ∈ R e a ∈ R+ {1}
• (k) = 0
• uk = kuk−1u
• (eu) = u eu
• (au) = u au ln a
• (ln u) =
u
u
• (loga u) =
u
u ln a
• (sen u) = u cos u
• (cos u) = −u sen u
• (tan u) = u
cos2 u
• (u + v) = u + v
• (uv) = u v + uv
•
u
v
=
u v − uv
v2

Exerc´ıcios 38
Exe 2.15
Calcule a derivada das seguintes fun¸c˜oes:
(a) f (x) = x2
ex2
(b) f (x) = (x − 1)(x2
+ 3x)
(c) f (x) =
cos x
1 − sen x
(d) f (x) = 3
(2x − 1)2
(e) f (x) = 3tg x
(f) f (x) = cos log2 x2
(g) f (x) = 1 − x2
ln x
(h) f (x) = x2
−
ln x2
x
Exe 2.16
Calcule, usando a regra da cadeia, (g ◦ f ) (1) sendo
f (x) = ex3−1 e g(x) = sen x2 .

Fun¸cão Derivada 39
Def 2.17
Seja f : Df −→ R uma fun¸cão. Seja D ⊆ Df o conjunto dos
pontos interiores de Df onde f é diferenciável.
Chamamos fun¸cão derivada de f à fun¸cão:
f : D −→ R
x −→ f (x)
Exe 2.18
Caracterize a fun¸cão derivada das seguintes fun¸cões:
(a) f (x) = x
(b) f (x) = |x|

Derivadas de ordem superior 40
Def 2.19
A f também se chama fun¸cão derivada de primeira ordem de f .
A partir de f podemos determinar a sua fun¸cão derivada, f ,
definida nos pontos onde f é diferenciável, tal que
f (x) = (f ) (x),
f é a chamada fun¸cão derivada de ordem dois ou fun¸cão derivada
de segunda ordem de f .
Dada a fun¸cão derivada de ordem n − 1 de f , f (n−1), a fun¸cão
derivada de ordem n é a fun¸cão f (n), cujo dom´ınio é o conjunto de
pontos onde f (n−1) é diferenciável e f (n)(x) := (f (n−1)) (x).
Exe 2.20
Seja f (x) = 1
x , cujo dom´ınio é R {0}. Por deriva¸cão sucessiva,
intua a expressão anal´ıtica de f (n)(x), ∀n ∈ N.

Método de indu¸cão matemática 41
Obs 2.21
Para provar que a expressão anal´ıtica de f (n)(x) que se obteve no
exerc´ıcio 2.20 está correta pode-se usar um método de prova
designado por método de indu¸cão matemática.
Def 2.22
Seja P(n) uma propriedade que depende de n ∈ N.
O método de indu¸cão matemática é uma técnica de demonstra¸cão
que tem como objetivo: mostrar que P(n) é verdadeira ∀n ∈ N.
Este método consiste em dois passos:
1 Passo de base: mostrar que P(1) é verdadeira;
2 Passo de indu¸cão (ou hereditariedade): assumindo que P(k) é
verdadeira, mostrar que P(k + 1) é verdadeira, para k ∈ N
arbitrário.

Método de indu¸cão matemática 42
Obs 2.23
1 P(k) chama-se hipótese de indu¸cão e P(k+1) tese de indu¸cão
2 Este método pode generalizar-se para situa¸cões onde se
pretenda mostrar que
P(n) é verdadeira ∀n ∈ Z, com n ≥ n0, n0 ∈ Z.
Para tal basta, no passo base tomar n0 em vez de 1 e no
passo de indu¸cão considerar k inteiro e k ≥ n0.
Exe 2.24
(a) Prove que a expressão anal´ıtica de f (n)(x) que se obteve no
exerc´ıcio 2.20 está correta.
(b) Prove que a soma dos n primeiros números naturais é dada
por n(1+n)
2

Exerc´ıcios 43
Exe 2.25
1 Considere a fun¸cão f (x) =
ex−1 − 1 se x < 1
sen(x − 1) se x ≥ 1
.
(a) Estude f quanto à continuidade em x = 1.
(b) Calcule as derivadas laterais f−(1) e f+(1).
(c) A fun¸cão f é diferenciável em x = 1? Justifique.
2 Considere a fun¸cão f definida por f (x) = x2 ln x + 11x − x2
2 .
Determine o valor de a ∈ R+ por forma a que a tangente ao
gráfico de f no ponto de abcissa x = a tenha declive m = 11.
3 Calcule a derivada das seguintes fun¸cões:
(a) f (x) = 2x2
−5
(b) f (x) = (1 + cos x)3
(c) f (x) =
ex
− 1
ex + 1
(d) f (x) = 3 sen2
x + 1
(e) f (x) = ln(ln x)
(f) f (x) = (5x)x
, com x > 0

C´alculo I 44
Fun¸c˜oes Inversas
Ricardo Pereira
Outubro de 2012

Inversa de uma fun¸cão 45
Def 3.1
f : Df → R é uma fun¸cão injetiva se, para todo o ∀x1, x2 ∈ Df ,
f (x1) = f (x2) ⇒ x1 = x2
Exe 3.2
Verifique se as fun¸cões f (x) = 2x − 1 e g(x) = x2 são injetivas.
Def 3.3
Seja f : Df ⊂ R → R uma fun¸cão injetiva. A fun¸cão
f −1 : CDf → R
y → x
onde x é tal que f (x) = y, é designada por fun¸cão inversa de f .
Dizemos que uma fun¸cão é invert´ıvel se admite inversa.

Consequências da defini¸cão de inversa 46
Obs 3.4
f é invert´ıvel sse f é injetiva
O contradom´ınio de f −1 é Df
∀x ∈ Df , f −1 ◦ f (x) = x
∀y ∈ CDf , f ◦ f −1 (y) = y
∀x ∈ Df , ∀y ∈ CDf , f (x) = y ⇔ x = f −1(y)
Os gráficos de f e f −1 são simétricos relativamente
à reta y = x
Exe 3.5
Caracterize a inversa das fun¸cões f (x) = 2x − 1 e g(x) = x−1
x+2.

Algumas propriedades das fun¸cões invert´ıveis 47
Prop 3.6
Se f :Df ⊂ R → R é estritamente monótona em Df , então
f é injetiva.
Prop 3.7
Se f :Df ⊂ R → R é estritamente crescente (resp. estritamente
decrescente) em Df , então f −1 é estritamente crescente (resp.
estritamente decrescente) em CDf .
Prop 3.8
Seja f uma fun¸cão cont´ınua e estritamente crescente
(resp. estritamente decrescente) num intervalo [a, b].
Sejam c, d ∈ R tais que f (a) = c e f (b) = d. Então:
(i) f −1 é estritamente crescente em [c, d]
(resp. estritamente decrescente em [d, c]);
(ii) f −1 é cont´ınua.

Inversa da fun¸cão exponencial 48
Def 3.9
Fun¸cão exponencial de base e: f : R −→ R
x −→ ex
onde e é o número de Neper, i.e., lim
n→+∞
1 + 1
n
n
= e.
Def 3.10
f é estritamente crescente, logo invert´ıvel. A sua inversa é a fun¸cão
f −1 : R+ −→ R
x −→ y = ln x
onde y = ln x sse ey = x, ∀y ∈ R, ∀x ∈ R+.
Obs 3.11
ln x lê-se logaritmo de x ou logaritmo neperiano de x

Gráficos das fun¸cões y = ex
e y = ln x 49
x
y
e
1
1
e
y = ln x
y = ex
y = x

Propriedades do logaritmo neperiano 50
Prop 3.12
Para todos x, y ∈ R+ e todo α ∈ R,
1 ln(xy) = ln x + ln y
2 ln(x
y ) = ln x − ln y
3 ln(xα) = α ln x
Exe 3.13
1 Prove que as propriedades anteriores são válidas.
2 Caracterize a inversa das fun¸cões:
(a) f (x) = e1−2x
(b) f (x) = 5 ln(x−3)−1
4

Inversa da fun¸cão exponencial de base a 51
Def 3.14
Fun¸cão exponencial de base a:
(a > 0, a = 1, a = e)
g : R −→ R
x −→ ax
Def 3.15
g é estrit. crescente se a > 1 e estrit. decrescente se a < 1.
Portanto g é invert´ıvel nos dois casos. A inversa de g é a fun¸cão
g−1 : R+ −→ R
x −→ y = loga x
onde y = loga x sse ay = x, ∀y ∈ R, ∀x ∈ R+.
Obs 3.16
loga x lê-se logaritmo de x na base a

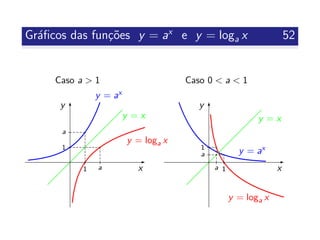
Gráficos das fun¸cões y = ax
e y = loga x 52
x
y
a
1
1
a
y = loga x
y = ax
y = x
Caso a > 1
x
y
a
1
1
a
y = loga x
y = ax
y = x
Caso 0 < a < 1

Propriedades dos logaritmos 53
Prop 3.17
Sejam x, y ∈ R+, α ∈ R e a, b ∈ R+ {1}
1 loga(xy) = loga x + loga y
2 loga(x
y ) = loga x − loga y
3 loga(xα) = α loga x
4 loga x = logb x
logb a
Exe 3.18
1 Prove que as propriedades anteriores são válidas.
2 Caracterize a inversa das fun¸cões:
(a) f (x) = log3(2 − x)
(b) f (x) = ex
ex +1

Fun¸cão seno 54
Def 3.19
Fun¸cão seno: sen : R −→ R
x −→ sen x
Prop 3.20
Propriedades da fun¸cão seno:
Dom´ınio: R
Contradom´ınio: [−1, 1]
Fun¸cão periódica de per´ıodo 2π, isto é,
sen x = sen(x + 2kπ), ∀x ∈ R e k ∈ Z
Fun¸cão ´ımpar
Não é injetiva

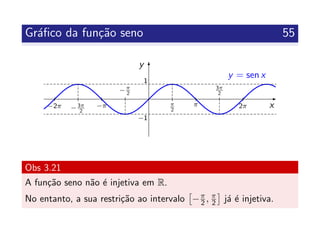
Gráfico da fun¸cão seno 55
x
y
π
2
−π
2
3π
2
−3π
2
π 2π−π−2π
y = sen x
1
−1
Obs 3.21
A fun¸cão seno não é injetiva em R.
No entanto, a sua restri¸cão ao intervalo −π
2 , π
2 já é injetiva.

Inversa da fun¸cão seno 56
Def 3.22
A restri¸cão principal da fun¸cão seno é a fun¸cão
f : [−π
2 , π
2 ] −→ R
x −→ sen x
que já é injetiva.
A inversa de f é chamada de fun¸cão arco seno,
denota-se por arcsen, e define-se do seguinte modo
arcsen : [−1, 1] −→ R
x −→ y = arcsen x
onde
y = arcsen x sse sen y = x, ∀x ∈ [−1, 1], ∀y ∈ −π
2 , π
2 .
Obs 3.23
arcsen x lê-se arco cujo seno é x

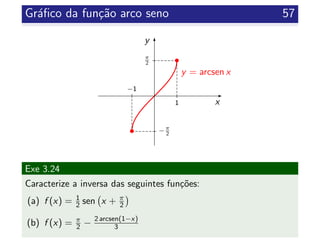
Gráfico da fun¸cão arco seno 57
x
y
•
1
π
2
•
−1
−π
2
y = arcsen x
Exe 3.24
Caracterize a inversa das seguintes fun¸cões:
(a) f (x) = 1
2 sen x + π
2
(b) f (x) = π
2 − 2 arcsen(1−x)
3

Fun¸cão cosseno 58
Def 3.25
Fun¸cão cosseno: cos : R −→ R
x −→ cos x
Prop 3.26
Propriedades da fun¸cão cosseno:
Dom´ınio: R
Contradom´ınio: [−1, 1]
cos x = cos(x + 2kπ), ∀x ∈ R e k ∈ Z
Fun¸cão par
Não é injetiva

Gráfico da fun¸cão cosseno 59
x
y
π
2
−π
2
3π
2
−3π
2
π
2π
−π
−2π
y = cos x
1
−1
Obs 3.27
A fun¸cão cosseno não é injetiva em R.
No entanto, a sua restri¸cão ao intervalo [0, π] já é injetiva.

Inversa da fun¸cão cosseno 60
Def 3.28
A restri¸cão principal da fun¸cão cosseno é a fun¸cão
f : [0, π] −→ R
x −→ cos x
A inversa de f é chamada de fun¸cão arco cosseno,
denota-se por arccos, e define-se do seguinte modo
arccos : [−1, 1] −→ R
x −→ y = arccos x
onde
y = arccos x sse cos y = x, ∀x ∈ [−1, 1], ∀y ∈ [0, π].
Obs 3.29
arccos x lê-se arco cujo cosseno é x

Gráfico da fun¸cão arco cosseno 61
x
y
•
1
π
2
•
−1
π
y = arccos x
Exe 3.30
(a) f (x) = 1
2+cos x
(b) f (x) = 2π − arccos x
2

Fun¸cão tangente 62
Def 3.31
Fun¸cão tangente: tg : D ⊂ R −→ R
x −→ tg x = sen x
cos x
Prop 3.32
Propriedades da fun¸cão tangente:
Dom´ınio: {x ∈ R : x = π
2 + kπ, k ∈ Z}
Contradom´ınio: R
Fun¸cão periódica de per´ıodo π, isto é,
tg x = tg(x + kπ), ∀x ∈ D e k ∈ Z
Fun¸cão ´ımpar
Não é injetiva

Gráfico da fun¸cão tangente 63
x
y
π
2
−π
2
3π
2
−3π
2
π 2π−π−2π
y = tg x
Obs 3.33
A fun¸cão tangente não é injetiva no seu dom´ınio.
2 , π
2 já é injetiva.

Inversa da fun¸cão tangente 64
Def 3.34
A restri¸cão principal da fun¸cão tangente é a fun¸cão
f : −π
2 , π
2 −→ R
x −→ tg x
A inversa de f é chamada de fun¸cão arco tangente,
denota-se por arctg, e define-se do seguinte modo
arctg : R −→ R
x −→ y = arctg x
onde
y = arctg x sse tg y = x, ∀x ∈ R, ∀y ∈ −π
2 , π
2 .
Obs 3.35
arctg x lê-se arco cuja tangente é x

Gráfico da fun¸cão arco tangente 65
x
y
y = arctg x
π
2
−π
2
Exe 3.36
(a) f (x) = tg π
2−x
(b) f (x) = π
2 − 2
3 arctg(1 − x)

Fun¸cão cotangente 66
Def 3.37
Fun¸cão cotangente: cotg : D ⊂ R −→ R
x −→ cotg x = cos x
sen x
Prop 3.38
Propriedades da fun¸cão cotangente:
Dom´ınio: {x ∈ R : x = kπ, k ∈ Z}
Contradom´ınio: R
Fun¸cão periódica de per´ıodo π, isto é,
cotg x = cotg(x + kπ), ∀x ∈ D e k ∈ Z
Fun¸cão ´ımpar
Não é injetiva

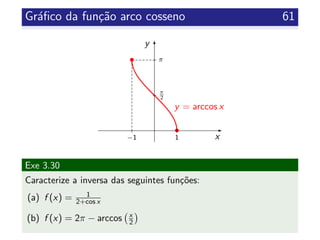
Gráfico da fun¸cão cotangente 67
x
y
π
2
−π
2
3π
2
−3π
2
π 2π−π−2π
y =cotg x
Obs 3.39
A fun¸cão cotangente não é injetiva no seu dom´ınio.
No entanto, a sua restri¸cão ao intervalo ]0, π[ já é injetiva.

Inversa da fun¸cão cotangente 68
Def 3.40
A restri¸cão principal da fun¸cão cotangente é a fun¸cão
f : ]0, π[ −→ R
x −→ cotg x
A inversa de f é chamada de fun¸cão arco cotangente,
denota-se por arccotg, e define-se do seguinte modo
arccotg : R −→ R
x −→ y = arccotg x
onde
y = arccotg x sse cotg y = x, ∀x ∈ R, ∀y ∈]0, π[.
Obs 3.41
arccotg x lê-se arco cuja cotangente é x

Gráfico da fun¸cão arco cotangente 69
x
y
y = arccotg x
π
π
2
Exe 3.42
(a) f (x) = 2 cotg x
3
(b) f (x) = π + arccotg x−1
2

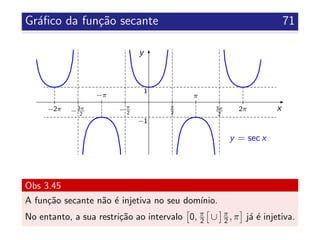
Fun¸cão secante 70
Def 3.43
Fun¸cão secante: sec : D ⊂ R −→ R
x −→ sec x = 1
cos x
Prop 3.44
Propriedades da fun¸cão secante:
Dom´ınio: {x ∈ R : x = π
2 + kπ, k ∈ Z}
Contradom´ınio: ] − ∞, −1] ∪ [1, +∞[
sec x = sec(x + 2kπ), ∀x ∈ D e k ∈ Z
Fun¸cão par
Não é injetiva
(sec x) = tg x sec x, ∀x ∈ D

Gráfico da fun¸cão secante 71
x
y
π
2
−π
2
3π
2
−3π
2
π
2π
−π
−2π
y = sec x
1
−1
Obs 3.45
A fun¸cão secante não é injetiva no seu dom´ınio.
No entanto, a sua restri¸cão ao intervalo 0, π
2 ∪ π
2 , π já é injetiva.

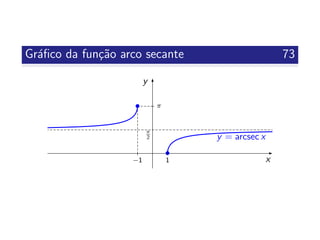
Inversa da fun¸cão secante 72
Def 3.46
A restri¸cão principal da fun¸cão secante é a fun¸cão
f : 0, π
2 ∪ π
2 , π −→ R
x −→ sec x
A inversa de f é chamada de fun¸cão arco secante,
denota-se por arcsec, e define-se do seguinte modo
arcsec : ] − ∞, −1] ∪ [1, +∞[ −→ R
x −→ y = arcsec x
onde, ∀x ∈] − ∞, −1] ∪ [1, +∞[, ∀y ∈ [0, π] π
2
y = arcsec x sse sec y = x
Obs 3.47
arcsec x lê-se arco cuja secante é x

Gráfico da fun¸cão arco secante 73
x
y
y = arcsec x
π
2
•
1
•
−1
π

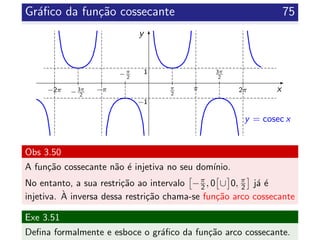
Fun¸cão cossecante 74
Def 3.48
Fun¸cão cossecante: cosec : D ⊂ R −→ R
x −→ cosec x = 1
sen x
Prop 3.49
Propriedades da fun¸cão cossecante:
Dom´ınio: {x ∈ R : x = kπ, k ∈ Z}
Contradom´ınio: ] − ∞, −1] ∪ [1, +∞[
cosec x = cosec(x + 2kπ), ∀x ∈ D e k ∈ Z
Fun¸cão ´ımpar
Não é injetiva
(cosec x) = − cotg x cosec x, ∀x ∈ D

Gráfico da fun¸cão cossecante 75
x
y
π
2
−π
2
3π
2
−3π
2
π 2π−π−2π
y = cosec x
1
−1
Obs 3.50
A fun¸cão cossecante não é injetiva no seu dom´ınio.
2 , 0 ∪ 0, π
2 já é
injetiva. À inversa dessa restri¸cão chama-se fun¸cão arco cossecante
Exe 3.51
Defina formalmente e esboce o gráfico da fun¸cão arco cossecante.

Fun¸cões inversas trigonométricas - resumo 76
Obs 3.52
Fun¸cão Dom´ınio Contradom´ınio
arcsen x [−1, 1] −π
2 , π
2
arccos x [−1, 1] [0, π]
arctg x R −π
2 , π
2
arccotg x R ]0, π[
arcsec x ] − ∞, −1] ∪ [1, +∞[ [0, π] π
2
arccosec x ] − ∞, −1] ∪ [1, +∞[ −π
2 , π
2 {0}

Algumas f´ormulas trigonom´etricas 77
Prop 3.53
1 sen2 x + cos2 x = 1
2 cosec2 x = 1 + cotg2 x, para x = kπ, k ∈ Z
3 sec2 x = 1 + tg2 x, para x = π
2 + kπ, k ∈ Z
4 cos(x − y) = cos x cos y + sen x sen y
5 cos(x + y) = cos x cos y − sen x sen y
6 sen(x − y) = sen x cos y − cos x sen y
7 sen(x + y) = sen x cos y + cos x sen y
8 cos(2x) = cos2 x − sen2 x
9 sen(2x) = 2 sen x cos x
10 cos2 x = 1+cos(2x)
2
11 sen2 x = 1−cos(2x)
2

Deriva¸cão da inversa de uma fun¸cão 78
Teo 3.54
Teorema da derivada da fun¸cão inversa
Sejam f :[a, b] −→ R uma fun¸cão estritamente monótona e
cont´ınua e f −1 a inversa de f . Se f é diferenciável em x0 ∈]a, b[ e
f (x0) = 0, então f −1 é diferenciável em y0 = f (x0) e
f −1
(y0) =
1
f (x0)
.
Exe 3.55
1 Sendo f : [1, 4] → R cont´ınua e estritamente crescente tal que
f (2) = 7 e f (2) = 2
3, calcule, caso exista, (f −1) (7).
2 Sabendo que f (x) = 4x3+x+2 é invert´ıvel, calcule f −1 (2).
3 Seja f (x) = x3. Determine f −1 (x) utilizando o teorema da
fun¸cão inversa.

Deriva¸cão das fun¸cões trigonométricas inversas 79
Obs 3.56
Resulta do teorema da derivada da fun¸cão inversa que:
1 (arcsen x) =
1
√
1 − x2
, ∀x ∈] − 1, 1[
2 (arccos x) = −
1
√
1 − x2
, ∀x ∈] − 1, 1[
3 (arctg x) =
1
1 + x2
, ∀x ∈ R
4 (arccotg x) = −
1
1 + x2
, ∀x ∈ R
Exe 3.57
Prove as fórmulas anteriores usando o teorema da derivada da
fun¸cão inversa.

Formulário de derivadas trigonométricas 80
Obs 3.58
Seja u uma fun¸cão de x
• (sen u) = u cos u • (cosec u) = −u cotg u cosec u
• (cos u) = −u sen u • (arcsen u) = u√
1−u2
• (tan u) = u sec2 u • (arccos u) = − u√
1−u2
• (cotg u) = −u cosec2 u • (arctg u) = u
1+u2
• (sec u) = u tg u sec u • (arccotg u) = − u
1+u2

Exerc´ıcios 81
Exe 3.59
1 Seja f (x) = ln(arcsen x), com x ∈]0, 1[.
Calcule f −1 (x) utilizando o teorema da fun¸cão inversa.
2 Calcule a derivada das seguintes fun¸cões:
(a) f (x) = 1 + x2
arctg x
(b) f (x) = arcsen 1
x2
(c) f (x) = arccotg sen 4x3
(d) f (x) = 3
√
arccos x
3 Considere a fun¸cão f (x) = arcsen(1 − x) +
√
2x − x2.
(a) Determine o dom´ınio de f .
(b) Mostre que f (x) = −
x
√
2x − x2

C´alculo I 82
Estudo anal´ıtico de fun¸c˜oes
Ricardo Pereira
Outubro de 2012

Extremos locais de uma fun¸cão 83
Def 4.1
Sejam f : Df ⊂ R −→ R e a ∈ Df .
a é um maximizante local de f e f (a) diz-se um máximo local
de f se existir δ > 0 tal que
f (a) ≥ f (x), ∀x ∈ Vδ(a) ∩ Df
a é um minimizante local de f e f (a) diz-se um m´ınimo local
de f se existir δ > 0 tal que
f (a) ≤ f (x), ∀x ∈ Vδ(a) ∩ Df
Aos máximos e m´ınimos locais chamamos extremos locais
Aos maximizantes e minimizantes locais chamamos
extremantes locais.

Extremos globais de uma fun¸cão 84
Def 4.2
Sejam f : Df ⊂ R −→ R e a ∈ Df .
a é um maximizante global de f e f (a) diz-se um máximo
global de f se
f (a) ≥ f (x), ∀x ∈ Df
a é um minimizante global de f e f (a) diz-se um m´ınimo
global de f se
f (a) ≤ f (x), ∀x ∈ Df
Aos máximos e m´ınimos globais chamamos extremos globais
Aos maximizantes e minimizantes globais chamamos
extremantes globais.

Condi¸cão necessária de existência de extremo 85
Prop 4.3
Seja f :]a, b[−→ R uma fun¸cão diferenciável em c ∈]a, b[.
Se c é um extremante local de f então f (c) = 0.
Ilustra¸cão gráfica:
x
y
c1
c2
a b
y = f (x)

Observa¸cões 86
Obs 4.4
1 O rec´ıproco da proposi¸cão do slide anterior não é verdadeiro.
De facto, existem fun¸cões com derivada nula em determinado
ponto e esse ponto não é extremante.
Por exemplo, f (x) = x3, no ponto x = 0.
2 Pode acontecer que a derivada de f não exista num dado
ponto x0, mas x0 ser extremante. Por exemplo:
f (x) = |x|, no ponto x0 = 0.
f (x) =
1
x2 se x = 0
0 se x = 0
, no ponto x0 = 0
Def 4.5
Seja f : Df −→ R uma fun¸cão diferenciável em c ∈ int(Df ). Se
f (c) = 0 dizemos que c é ponto cr´ıtico de f .

Teorema de Rolle 87
Teo 4.6
Seja f uma fun¸cão cont´ınua em [a, b] e diferenciável em ]a, b[.
Se f (a) = f (b), então existe c ∈]a, b[ tal que f (c) = 0
Ilustra¸cão Gráfica:
x
y
c
a b
y = f (x)

Corolários do Teorema de Rolle 88
Cor 4.7
(i) Entre dois zeros de f existe pelo menos um zero de f .
(ii) Entre dois zeros consecutivos de f existe, no máximo, um
zero de f .
Exe 4.8
1 Mostre que se a > 0 a equa¸cão x3 + ax + b = 0 não pode ter
mais que uma raiz real, qualquer que seja b ∈ R.
2 Mostre que a fun¸cão definida por f (x) = sen x + x tem um
único zero no intervalo [−π, π].
3 Seja f (x) =
x ln x se x > 0
sen x se x ≤ 0
Mostre que é poss´ıvel aplicar o Teorema de Rolle a f em [0, 1]
e determine o ponto c ∈ [0, 1[ tal que f (c) = 0.

Teorema de Lagrange 89
Teo 4.9
Então, existe c ∈]a, b[ tal que
f (c) =
f (b) − f (a)
b − a
.
Ilustra¸cão Gráfica:
x
y
ca
f (a)
b
f (b)
y = f (x)

Exerc´ıcios 90
Exe 4.10
1 Seja f (x) =



x2 sen 1
x se x < 0
0 se x = 0
π
2 − arctg 1
x se x > 0
(a) Estude f quanto à continuidade em x = 0.
(b) Mostre que existe pelo menos um c ∈ − 2
π , 0
tal que f (c) = 2
π .
2 Seja f (x) = arcsen(ln x).
(b) Mostre que existe pelo menos um c ∈ ]1, e[
tal que f (c) = π
2(e−1) .
3 Seja f (x) = x
x+1.
Determine, caso existam, os valores de c ∈ R para os quais a
tangente ao gráfico de f no ponto (c, f (c)) seja paralela à
reta que passa pelos pontos (1, f (1)) e (3, f (3)).

Consequências do Teorema de Lagrange 91
Prop 4.11
Sejam I ⊂ R um intervalo e f : I −→ R uma fun¸cão cont´ınua em I
e diferenciável em int(I). Então
(i) Se f (x) = 0, ∀x ∈ int(I), então f é constante em I.
(ii) Se f (x) ≥ 0, ∀x ∈ int(I), então f é crescente em I.
(iii) Se f (x) ≤ 0, ∀x ∈ int(I), então f é decrescente em I.
(iv) Se f (x) > 0, ∀x ∈ int(I), então f é estritamente crescente
em I.
(v) Se f (x) < 0, ∀x ∈ int(I), então f é estritamente decrescente
em I.

Cond. suficientes para a existência de extremo 92
Prop 4.12
Seja f : Df −→ R uma fun¸cão cont´ınua em [a, b] ⊂ Df e
diferenciável em ]a, b[, exceto possivelmente em c ∈]a, b[. Então,
(i) se f (x) > 0, ∀x < c e f (x) < 0, ∀x > c,
então f (c) é um máximo local de f .
(ii) se f (x) < 0, ∀x < c e f (x) > 0, ∀x > c,
então f (c) é um m´ınimo local de f .
Prop 4.13
Seja c um ponto cr´ıtico de f num intervalo ]a , b[. Admitamos que
f é cont´ınua em ]a, b[ e f existe e é finita em todo o ponto de
]a, b[. Então verificam-se as condi¸cões seguintes:
(i) se f (c) < 0, então f admite em c um máximo local.
(ii) se f (c) > 0, então f admite em c um m´ınimo local.

Exerc´ıcios 93
Exe 4.14
1 Seja f (x) = ln x
x .
(b) Estude f quanto à monotonia e existência de extremos locais.
2 Mostre que f (x) = ex
ex +1 é estritamente crescente em R.
3 Seja f (x) = x
x+1 + ln(x + 1).
(b) Estude f quanto à monotonia e existência de extremos locais.
4 Seja h(x) = x + 2 sen x − 1.
(a) Mostre que h tem pelo menos um zero no intervalo ]0, π
2 [.
(b) Prove que a equa¸cão x + 2 sen x − 1 = 0 tem uma única
solu¸cão no intervalo ]0, π
2 [.

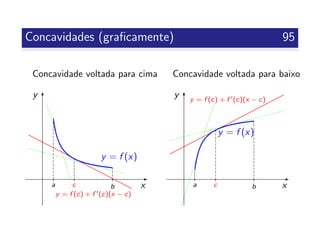
Concavidades 94
Def 4.15
Seja f uma fun¸cão diferenciável em ]a, b[.
Dizemos que o gráfico de f tem a concavidade voltada para
cima em ]a, b[ se, para todo o c ∈]a, b[,
f (x) > f (c) + f (c)(x − c) , para todo o x ∈]a, b[{c} ,
isto é, o gráfico de f está situado acima da tangente ao
gráfico de f no ponto (c, f (c)).
Dizemos que o gráfico de f tem a concavidade voltada para
baixo em ]a, b[ se, para todo o c ∈]a, b[,
f (x) < f (c) + f (c)(x − c) , para todo o x ∈]a, b[{c} ,
isto é, o gráfico de f está situado abaixo da tangente ao
gráfico de f no ponto (c, f (c)).

Concavidades (graﬁcamente) 95
x
y
ca b
y = f (x)
y = f (c) + f (c)(x − c)
Concavidade voltada para cima
x
y
ca b
y = f (x)
y = f (c) + f (c)(x − c)
Concavidade voltada para baixo

Concavidades e pontos de inflexão 96
Prop 4.16
Seja f uma fun¸cão diferenciável em ]a, b[ tal que existe e é finita
f (x), para todo o x ∈]a, b[.
(i) Se f (x) > 0, ∀x ∈]a, b[, então o gráfico de f tem
concavidade voltada para cima em ]a, b[.
(ii) Se f (x) < 0, ∀x ∈]a, b[, então o gráfico de f tem
concavidade voltada para baixo em ]a, b[.
Def 4.17
Seja f :]a, b[−→ R uma fun¸cão duas vezes diferenciável excepto
possivelmente em c ∈]a, b[. Dizemos que o ponto de coordenadas
(c, f (c)) é um ponto de inflexão do gráfico de f se f (x) muda de
sinal em x = c.

Exerc´ıcios 97
Exe 4.18
1 Estude o sentido das concavidades e determine, se existirem,
os pontos de inflexão da fun¸cão f (x) = x4 − 8x3 + 12x − 4.
2 Seja f (x) = ln(2ex − 1).
(b) Mostre que f tem a concavidade voltada para baixo em todo o
seu dom´ınio.

Teorema de Cauchy 98
Teo 4.19
Sejam f e g duas fun¸cões cont´ınuas em [a, b] e diferenciáveis em
]a, b[. Se g (x) = 0, para todo o x ∈]a, b[, então existe c ∈]a, b[
tal que
f (c)
g (c)
=
f (b) − f (a)
g(b) − g(a)
.
Obs 4.20
Do Teorema de Cauchy pode estabelecer-se uma regra — Regra de
Cauchy — de grande utilidade no cálculo de limites quando
ocorrem indetermina¸cões do tipo ∞
∞ ou 0
0 .
Nos cinco slides seguintes enunciam-se as várias formas dessa
regra.

Regra de Cauchy (versão 1) 99
Prop 4.21
Sejam f e g fun¸cões diferenciáveis em I =]a, b[ tais que, ∀x ∈ I,
g(x) = 0 e g (x) = 0. Se
lim
x→a+
f (x) e lim
x→a+
g(x) são ambos nulos ou ambos infinitos
e existe o limite
lim
x→a+
f (x)
g (x)
então
lim
x→a+
f (x)
g(x)
= lim
x→a+
f (x)
g (x)
.

Prop 4.22
Sejam f e g fun¸cões diferenciáveis em I =]a, b[ tais que, ∀x ∈ I,
g(x) = 0 e g (x) = 0. Se
lim
x→b−
f (x) e lim
x→b−
e existe o limite
lim
x→b−
f (x)
g (x)
então
lim
x→b−
f (x)
g(x)
= lim
x→b−
f (x)
g (x)
.

Prop 4.23
Sejam I =]a, b[ e c ∈ I. Sejam f e g fun¸cões definidas em I e
diferenciáveis em I {c}, tais que g(x) = 0, ∀x ∈ I {c}.
Se g (x) = 0, ∀x ∈ I {c},
lim
x→c
f (x) e lim
x→c
e existe o limite
lim
x→c
f (x)
g (x)
então
lim
x→c
f (x)
g(x)
= lim
x→c
f (x)
g (x)
.

Prop 4.24
Sejam f e g fun¸cões definidas em I =]a, +∞[ e diferenciáveis em
I, com g(x) = 0, ∀x ∈ I. Se g (x) = 0, ∀x ∈ I,
lim
x→+∞
f (x) e lim
x→+∞
e
existe lim
x→+∞
f (x)
g (x)
então
lim
x→+∞
f (x)
g(x)
= lim
x→+∞
f (x)
g (x)

Prop 4.25
Sejam f e g fun¸cões definidas em I =] − ∞, b[ e diferenciáveis em
I, com g(x) = 0, ∀x ∈ I. Se g (x) = 0, ∀x ∈ I,
lim
x→−∞
f (x) e lim
x→−∞
e
existe lim
x→−∞
f (x)
g (x)
então
lim
x→−∞
f (x)
g(x)
= lim
x→−∞
f (x)
g (x)

Exerc´ıcios 104
Exe 4.26
1 Calcule, caso existam, os seguintes limites:
(a) lim
x→0
2 arcsen x
3x
(b) lim
x→1
1 − x
ln(2 − x)
(c) lim
x→0
x2
arctg x
(d) lim
x→+∞
ln x
x3
(e) lim
x→0−
x2
ln(−x)
(f) lim
x→−∞
xe
1
x
(g) lim
x→0
xe
1
x2
(h) lim
x→1+
(ln x)ln x
2 Mostre que existe
lim
x→+∞
x − sen x
x + sen x
,
mas n˜ao pode aplicar-se para o seu c´alculo a regra de Cauchy.

Assintotas 105
Def 4.27
Seja f tal que ]a, +∞[⊂ Df , para algum a ∈ R. Dizemos que
a reta de equa¸cão y = mx + b é uma assintota ao gráfico de f
à direita ou quando x → +∞ se lim
x→+∞
[f (x)−(mx + b)] = 0
Seja f tal que ] − ∞, a[⊂ Df , para algum a ∈ R. Dizemos que
a reta de equa¸cão y = mx + b é uma assintota ao gráfico de f
à esquerda ou quando x → −∞ se lim
x→−∞
[f (x)−(mx + b)] = 0
Quando lim
x→+∞
f (x) = b ou lim
x→−∞
f (x) = b diz-se que y = b
é uma assintota horizontal ao gráfico de f
A reta de equa¸cão x = a diz-se uma assintota vertical ao
gráfico de f se se verificar uma das condi¸cões:
lim
x→a+
f (x) = +∞ ou lim
x→a+
f (x) = −∞ ou
lim
x→a−
f (x) = +∞ ou lim
x→a−
f (x) = −∞ .

Carateriza¸cão das assintotas não verticais 106
Prop 4.28
Seja f tal que ]a, +∞[⊂ Df , para algum a∈R. A reta de equa¸cão
y = mx + b é uma assintota ao gráfico de f à direita se e só se
existem e são finitos os limites lim
x→+∞
f (x)
x e lim
x→+∞
[f (x) − mx].
Nesse caso, temos
m = lim
x→+∞
f (x)
x e b = lim
x→+∞
(f (x) − mx) .
Prop 4.29
Seja f tal que ] − ∞, a[⊂ Df , para algum a∈R. A reta de equa¸cão
y = mx + b é uma assintota ao gráfico de f à esquerda se e só se
existem e são finitos os limites lim
x→−∞
f (x)
x e lim
x→−∞
[f (x) − mx].
Nesse caso, temos
m = lim
x→−∞
f (x)
x e b = lim
x→−∞
(f (x) − mx) .

Exerc´ıcios 107
Exe 4.30
1 Determine o dom´ınio e, caso existam, as assintotas ao gráfico
das seguintes fun¸cões:
(a) f (x) = π
2 − arctg 1
x
(b) f (x) = x
x+1 + ln(x + 1)
(c) f (x) = x + arctg x
(d) f (x) = 1−cos(3x)
x−2
2 Considere a fun¸cão f definida em R {0} por
f (x) =
ln x
x se x > 0
xe
1
x se x < 0
Determine, caso existam, as assintotas ao gráfico de f .

Esbo¸co do gráfico de uma fun¸cão 108
Obs 4.31
Para esbo¸car o gráfico de uma fun¸cao deve-se ter em conta:
o dom´ınio da fun¸cão
os pontos de interse¸cão com os eixos OX e OY
o sinal da fun¸cão
os pontos de descontinuidade
as assintotas ao gráfico
os intervalos de monotonia
os extremantes locais
os pontos de inflexão e as concavidades.

Exerc´ıcios 109
Exe 4.32
Considere a fun¸cao f definida por f (x) =
x2
x2 − 1
.
(b) Calcule os zeros de f .
(c) Determine a fun¸cão derivada de f .
(d) Estude f quanto à monotonia.
(e) Calcule, caso existam, os extremos locais de f .
(f) Estude os intervalos de concavidade de f .
(g) Determine, caso existam, as assintotas ao gráfico de f .
(h) Esboce o gráfico da fun¸cão f .

C´alculo I 110
Integrais indeﬁnidos
Ricardo Pereira
Outubro de 2012

Primitiva de uma fun¸cão 111
Def 5.1
Seja f : I −→ R uma fun¸cão, onde I é um intervalo não
degenerado de R.
Chama-se primitiva ou antiderivada de f a toda a fun¸cão F
diferenciável em I tal que, para todo o x ∈ I,
F (x) = f (x).
Se f admite uma primitiva em I dizemos que f é primitivável em I.
Obs 5.2
Caso I = [a, b], dizer que F é diferenciável em I significa que,
para todo o x ∈]a, b[, F é diferenciável em x e que existem e
são finitas F+(a) e F−(b).
Conven¸cões análogas para I = [a, b[ ou I =]a, b].
Toda a primitiva de uma fun¸cão é uma fun¸cão cont´ınua.

Primitiva de uma fun¸cão (cont.) 112
Exe 5.3
Indique uma primitiva das seguintes fun¸cões (no intervalo indicado)
(a) f (x) = 2x, em R
(b) f (x) = ex , em R
(c) f (x) = cos x, em R
(d) f (x) = 1
x , em R+
Prop 5.4
Seja f : I → R uma fun¸cão e F : I → R uma primitiva de f em I.
Então, para cada C ∈ R, G(x) = F(x) + C é também uma
primitiva de f em I.
Prop 5.5
Se F : I → R e G : I → R são duas primitivas de f : I → R, então
existe C ∈ R tal que F(x) − G(x) = C, para todo o x ∈ I.

Integral Indefinido 113
Def 5.6
À fam´ılia de todas as primitivas de uma fun¸cão f chamamos
integral indefinido de f . Denota-se esse conjunto de fun¸cões por
f (x) dx
A f chamamos fun¸cão integranda e a x variável de integra¸cão
Obs 5.7
Atendendo à segunda proposi¸cão do slide anterior,
se F for uma primitiva de f , então
f (x) dx = F(x) + C, C ∈ R

Alguns Integrais Indeﬁnidos Imediatos 114
Obs 5.8
1 xp
dx =
xp+1
p + 1
+ C , C ∈ R, p ∈ R {−1}
2
1
x
dx = ln | x | +C , C ∈ R (onde x ∈ R+
ou x ∈ R−
)
3 ex
dx = ex
+ C , C ∈ R
4 ax
dx =
ax
ln a
+ C , C ∈ R, a ∈ R+
{1}
5 sen x dx = − cos x + C , C ∈ R
6 cos x dx = sen x + C , C ∈ R

Alguns Integrais Indeﬁnidos Imediatos (cont.) 115
Obs 5.8 (cont.)
7 sec2
x dx = tg x + C , C ∈ R
8 cosec2
x dx = − cotg x + C , C ∈ R
9
1
√
1 − x2
dx = arcsen x + C , C ∈ R
10
1
1 + x2
dx = arctg x + C , C ∈ R
11 sec x tg x dx = sec x + C , C ∈ R
12 cosec x cotg x dx = − cosec x + C , C ∈ R

Exerc´ıcios 116
Prop 5.9
Sejam f e g fun¸cões definidas em I e α, β ∈ R não
simultaneamente nulos.
Se f e g são primitiváveis em I, então αf +βg é primitivável em I e
(αf (x) + βg(x)) dx = α f (x) dx + β g(x) dx .
Exe 5.10
Calcule:
(a) (2x
− 3 sen x) dx
(b) (x + 3)x2
dx
(c)
x + 3
x2
dx
(d)
5
√
x3 dx

Fórmula para a Primitiva¸cão Imediata 117
Prop 5.11
Sejam I e J dois intervalos de números reais, f : I → R uma
fun¸cão primitivável e g : J → R uma fun¸cão tal que a composta
f ◦ g está definida.
Se g é diferenciável em J, então (f ◦ g)g é primitivável e tem-se
f (g(x))g (x) dx = F(g(x)) + C , C ∈ R ,
onde F é uma primitiva de f .
Exemplo de aplica¸cão
2x cos(x2
) dx = sen(x2
) + C , C ∈ R

Lista de Integrais Indefinidos Imediatos 118
Obs 5.12
(Esta lista generaliza os slides 145 e 115, e é uma consequência da Prop 5.11)
Seja u uma fun¸cão de x
1 u up
dx =
up+1
p + 1
+ C , C ∈ R, p ∈ R {−1}
2
u
u
dx = ln |u| + C , C ∈ R
3 u eu
dx = eu
+ C , C ∈ R
4 u au
dx =
au
ln a
+ C , C ∈ R, a ∈ R+
{1}
5 u sen u dx = − cos u + C , C ∈ R
6 u cos u dx = sen u + C , C ∈ R

Lista de Integrais Indeﬁnidos Imediatos (cont.) 119
Obs 5.12 (cont.)
7 u sec2
u dx = tg u + C , C ∈ R
8 u cosec2
u dx = − cotg u + C , C ∈ R
9
u
√
1 − u2
dx = arcsen u + C , C ∈ R
10
u
1 + u2
dx = arctg u + C , C ∈ R
11 u sec u tg u dx = sec u + C , C ∈ R
12 u cosec u cotg u dx = − cosec u + C , C ∈ R

Exerc´ıcios 120
Exe 5.13
Calcule os seguintes integrais indeﬁnidos:
(a)
x4
1 + x5
dx
(b) sen(
√
2x) dx
(c) x7x2
dx
(d) tg x dx
(e)
ln x
x
dx
(f)
5
x ln3
x
dx
(g)
1
x ln x
dx
(h)
1
x2 + 9
dx
(i) sen x cos5
x dx
(j) etg x
sec2
x dx
(k)
3x
√
1 − x4
dx
(l)
x3
√
1 − x4
dx

Exerc´ıcios (cont.) 121
Exe 5.14
1 Determine a fun¸cão f : R → R tal que
f (x) =
2ex
3 + ex
e f (0) = ln 4
2 Sabendo que a fun¸cão f satisfaz a igualdade
f (x) dx = sen x − x cos x −
1
2
x2
+ c, c ∈ R,
determinar f π
4 .
3 Determine a primitiva da fun¸cão f (x) =
1
x2
+ 1 que se anula
no ponto x = 2.

Primitiva¸cão por Partes 122
Prop 5.15
Sejam u e v fun¸cões de x diferenciáveis em I. Então
u v dx = uv − uv dx
Exemplo de aplica¸cão
x
u
ln x
v
dx =
x2
2
ln x −
x2
2
1
x
dx
=
x2
2
ln x −
x
2
dx
=
x2
2
ln x −
x2
4
+ C , C ∈ R .

Observa¸cões sobre a Primitiva¸cão por Partes 123
Obs 5.16
Esta fórmula é útil sempre que a fun¸cão integranda se pode
escrever como o produto de duas fun¸cões e, além disso, é
conhecida uma primitiva de pelo menos uma delas.
Sabendo primitivar apenas uma das fun¸cões, escolhe-se essa
para primitivar e deriva-se a outra fun¸cão.
Quando conhecemos uma primitiva de cada uma das fun¸cões,
devemos escolher para derivar a fun¸cão que mais se simplifica
por deriva¸cão. Por vezes essa escolha é indiferente.
Por vezes é necessário efetuar várias aplica¸cões sucessivas da
fórmula de integra¸cão por partes.
Por vezes obtém-se novamente o integral que se pretende
determinar. Nesses casos, interpreta-se a igualdade obtida
como uma equa¸cão em que a incógnita é integral que se
pretende determinar.

Exerc´ıcios 124
Exe 5.17
Calcule, usando a técnica de integra¸cão por partes, os seguintes
integrais indefinidos:
(a) x cos x dx
(b) e−3x
(2x + 3) dx
(c) arctg x dx
(d) x3
ln x dx
(e) x3
ex2
dx
(f) e2x
sen x dx
(g) sen(ln x) dx
(h) ln2
x dx

Primitiva¸cão de fun¸cões trigonométricas 125
Obs 5.18
1 Potências ´ımpares de sen x ou cos x
Destaca-se uma unidade à potência ´ımpar e o fator resultante
passa-se para a co-fun¸cão usando sen2 x + cos2 x = 1.
2 Potências pares de sen x ou cos x
Passam-se para o arco duplo através das fórmulas
cos2 x = 1+cos(2x)
2 ou sen2 x = 1−cos(2x)
2
3 Produtos onde existem fatores tipo sen (mx) ou cos (nx)
Aplicam-se as fórmulas
• sen x sen y = 1
2 cos(x − y) − cos(x + y)
• cos x cos y = 1
2 cos(x + y) + cos(x − y)
• sen x cos y = 1
2 sen(x + y) + sen(x − y)

Primitiva¸cão de fun¸cões trigonométricas 126
Obs 5.18 (cont.)
4 Potências pares e ´ımpares de tan x ou cotg x
Destaca-se tan2 x ou cotg2 x e aplicam-se as fórmulas
tan2 x = sec2 x − 1 ou cotg2 x = cosec2 x − 1
5 Potências pares de sec x ou cosec x
Destaca-se sec2 x ou cosec2 x e ao fator resultante aplicam-se
as fórmulas
sec2 x = 1 + tan2 x ou cosec2 x = 1 + cotg2 x
6 Potências ´ımpares de sec x ou cosec x
Destaca-se sec2 x ou cosec2 x e primitiva-se por partes
escolhendo esse fator para primitivar.

Exerc´ıcios 127
Exe 5.19
(a) cos2
x dx
(b) sen3
x dx
(c) tan6
x dx
(d) sen4
x dx
(e) sec3
x dx
(f) sen x cos2
x dx
(g) sen5
x cos2
x dx
(h) cos x cos(5x) dx
(i) sen(3x) cos(4x) dx
(j) sen(2x) sen(−3x) dx

Primitiva¸cão por Substitui¸cão 128
Prop 5.20
Sejam I e J intervalos de R, f : I −→ R uma fun¸cão primitivável e
ϕ : J −→ R uma fun¸cão diferenciável e invert´ıvel tal que ϕ(J) ⊂ I.
Então a fun¸cão (f ◦ ϕ)ϕ é primitivável e, sendo H uma primitiva
de (f ◦ ϕ)ϕ , tem-se que H ◦ ϕ−1 é uma primitiva de f .
Obs 5.21
Na prática, quando calculamos uma primitiva recorrendo à
Proposi¸cão anterior, usando a mudan¸ca de variável x = ϕ(t),
escrevemos, por abuso de linguagem,
f (x) dx = f (ϕ(t))ϕ (t) dt = H(ϕ−1
(x)) + C , C ∈ R .

Exemplo 129
Exemplo de aplica¸cão da técnica de primitiva¸cão por substitui¸cão
1
1 +
√
2x
dx
Substitui¸cão de variável:
√
2x = t, donde resulta x = t2
2 , t ≥ 0.
ϕ(t) = t2
2 é diferenciável e invert´ıvel em R+
0 e ϕ (t) = t. Assim
1
1 +
√
2x
dx =
t
1 + t
dt
= 1 −
1
1 + t
dt
= t − ln |1 + t| + C , C ∈ R
=
√
2x − ln(1 +
√
2x) + C , C ∈ R .

Primitiva¸cão de fun¸cões envolvendo radicais 130
Obs 5.22
As substitui¸cões trigonométricas dadas na seguinte tabela
permitem transformar a primitiva¸cão de uma fun¸cão que envolve
radicais na primitiva¸cão de uma fun¸cão trigonométrica.
fun¸cão com o radical substitui¸cão
√
a2 − b2x2, a, b > 0 x = a
b sen t, com t ∈] − π
2 , π
2 [
√
a2 + b2x2, a, b > 0 x = a
b tan t, com t ∈] − π
2 , π
2 [
√
b2x2 − a2, a, b > 0 x = a
b sec t, com t ∈]0, π
2 [

Exerc´ıcios 131
Exe 5.23
Calcule, usando a técnica de integra¸cão por substitui¸cão, os
seguintes integrais indefinidos:
(a) x2
√
1 − x dx
(b) x(2x + 5)10
dx
(c)
1
√
ex − 1
dx
(d)
√
x
1 + 3
√
x
dx
(e) x2
4 − x2 dx
(f)
1
x2
√
x2 − 7
dx
(g)
1
x
√
x2 + 4
dx
(h)
1
x2
√
9 − x2
dx

Primitiva¸cão de Fun¸cões Racionais 132
Def 5.24
Uma fun¸cão cuja expressão anal´ıtica admite a forma
N(x)
D(x)
onde N e D são polinómios em x com coeficientes reais e D é não
nulo, diz-se uma fun¸cão racional.
Caso grau(N) < grau(D) dizemos que N(x)
D(x) é uma fra¸cão própria.
Prop 5.25
Se grau(N) ≥ grau(D), então existem polinómios Q e R tais que
N(x) = D(x)Q(x) + R(x),
com grau(R) < grau(D).
A Q e R chamamos quociente e resto da divisão de N por D,
respetivamente.

Primitiva¸cão de Fun¸cões Racionais (cont.) 133
Obs 5.26
Assim, caso grau(N) ≥ grau(D),
N(x)
D(x)
= Q(x) +
R(x)
D(x)
polinómio fra¸cão própria
Como
N(x)
D(x)
dx = Q(x) dx +
R(x)
D(x)
dx ,
e a primitiva¸cão de fun¸cões polinomiais é imediata, a primitiva¸cão
de fun¸cões racionais reduz-se à primitiva¸cão de fra¸cões próprias,
que por sua vez se pode reduzir à primitiva¸cão de fra¸cões simples.

Fra¸cões simples 134
Def 5.27
Chamamos fra¸cão simples a toda a fra¸cão do tipo
A
(x − α)p
ou
Bx + C
(x2 + βx + γ)q
,
onde p, q ∈ N, A ∈ R {0}, B, C ∈ R não simultaneamente nulos
e α, β, γ ∈ R são tais que β2 − 4γ < 0.
Exemplos de fra¸cões simples
2
x − 1
,
1
x2
,
x − 2
x2 + x + 1
,
1
(x2 + x + 2)3
Prop 5.28
Toda a fra¸cão própria pode ser decomposta numa soma de fra¸cões
simples.

Decompor fra¸cões próprias em fra¸cões simples 135
Obs 5.29
Fra¸cão a decompor:
R(x)
D(x)
, com grau(R) < grau(D)
Procedimento
1 Decompor D(x) em fatores irredut´ıveis:
D(x)=a(x−α1)p1. . .(x−αn)pn (x2+β1x+γ1)q1. . .(x2+βmx+γm)qm
onde a ∈ R {0}, pi , qj ∈ N, αi , βj , γj ∈ R, com βj − 4γj < 0,
para i = 1, . . . , n e j = 1, . . . , m.
2 Fazer corresponder a cada factor de D(x) uma determinada
fra¸cão simples de acordo com o seguinte:
(i) Ao fator de D(x) do tipo (x − α)r
(r ∈ N) corresponde
A1
x − α
+
A2
(x − α)2
+ · · · +
Ar
(x − α)r
onde A1, . . . , Ar são constantes reais a determinar.

Decompor fra¸cões próprias em fra¸cões simples 136
Procedimento (cont.)
(ii) Ao fator de D(x) do tipo
(x2
+ βx + γ)s
, com β2
− 4γ < 0 e s ∈ N
corresponde
B1x + C1
x2 + βx + γ
+
B2x + C2
(x2 + βx + γ)2
+ · · · +
Bsx + Cs
(x2 + βx + γ)s
onde Bi , Ci são constantes reais a determinar, i = 1, . . . , s.
3 Escrever R(x)
D(x) como soma dos elementos simples identificados
no ponto anterior e determinar as constantes que neles
ocorrem, usando o método dos coeficientes indeterminados.

Primitiva¸cão de Fra¸cões Simples 137
Primitiva¸cão de Fra¸cões Simples
1 Fra¸cão do tipo:
A
(x − α)r
Se r = 1,
A
x − α
dx = A ln |x − α| + C, C ∈ R
Se r = 1,
A
(x − α)r
dx =
A(x − α)−r+1
−r + 1
+ C, C ∈ R
2 Fra¸cão do tipo:
Bx + C
(x2 + βx + γ)s
Reduz-se à primitiva¸cão de fra¸cões do tipo (i) ou (ii):
(i)
t
(1 + t2)s
(ii)
1
(1 + t2)s

Primitiva¸cão de Fra¸cões Simples 138
Primitiva¸cão das fra¸cões do tipo (i) e (ii) do slide anterior
(i) Fra¸cão do tipo:
t
(1 + t2)s
Se s = 1,
t
1 + t2
dt =
1
2
ln |1 + t2
| + C, C ∈ R
Se s = 1,
t
(1 + t2)s
dt =
(1 + t2)−s+1
2(−s + 1)
+ C, C ∈ R
(ii) Fra¸cão do tipo:
1
(1 + t2)s
Se s = 1,
1
1 + t2
dt = arctg t + C, C ∈ R
Se s = 1, aplica-se o método de primitiva¸cão por partes
recursivamente, partindo de
1
1 + t2
dt.

Exerc´ıcios 139
Exe 5.30
(a)
x
x2 − 5x + 6
dx
(b)
2x − 1
(x − 2)(x − 3)(x + 1)
dx
(c)
x + 1
x3 − 1
dx
(d)
x5 + x4 − 8
x3 − 4x
dx
(e)
x + 2
x(x2 + 4)
dx
(f)
3x − 1
x3 + x
dx
(g)
x + 1
x2 + 4x + 5
dx
(h)
5x − 4
x(x2 − 2x + 2)
dx

C´alculo I 140
Integral deﬁnido
Ricardo Pereira
Novembro de 2012

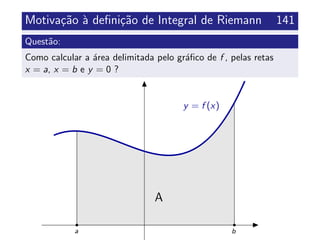
Motiva¸cão à defini¸cão de Integral de Riemann 141
Questão:
Como calcular a área delimitada pelo gráfico de f , pelas retas
x = a, x = b e y = 0 ?
y = f (x)
A
ba

´Area calculada por defeito 142
y y = f (x)
x0 = a b = x6
x1 x2 x3 x4 x5
Am =
6
i=1
mi (xi − xi−1)
mi =min {f (x): x ∈ [xi−1, xi ]}
m1
m2
m5
m6
m3
m4

´Area calculada por excesso 143
y
y = f (x)
x0 = a b = x6
x1 x2 x3 x4 x5
AM =
6
i=1
Mi (xi − xi−1)
Mi =max {f (x): x ∈ [xi−1, xi ]}
M6
M1
M2
M3
M5
M4

Outra aproxima¸c˜ao para o valor da ´area 144
x
y
y = f (x)
x0 = a b = x6
x1 x2 x3 x4 x5
A∗
=
6
i=1
f (x∗
i )(xi − xi−1)
Notar que:
Am ≤ A∗
≤ AM
x∗
1
x∗
2 x∗
3 x∗
4 x∗
5 x∗
6
f (x∗
1 )
f (x∗
3 )
f (x∗
4 )
f (x∗
5 )
f (x∗
6 )
f (x∗
2 )

Parti¸cão de um intervalo 145
Def 6.1
Chama-se parti¸cão de [a, b] a todo o subconjunto finito
de [a, b]
P = {x0, x1, . . . , xn}
tal que a ≡ x0 < x1 < · · · < xn ≡ b.
Chama-se diâmetro de P, e denota-se por ∆P, à maior das
amplitudes dos intervalos [xi−1, xi ], i = 1, 2, . . . , n, isto é
∆P = max {xi − xi−1 : i = 1, 2, . . . , n} .
Chama-se sele¸cão de P a todo o conjunto
C = {x∗
1 , x∗
2 , . . . , x∗
n }
tal que x∗
1 ∈ [x0, x1], x∗
2 ∈ [x1, x2], . . . , x∗
n ∈ [xn−1, xn].

Soma de Riemann 146
Def 6.2
Sejam f : [a, b] → R, P = {x0, x1, . . . , xn} uma parti¸cão de [a, b] e
C = {x∗
1 , x∗
2 , . . . , x∗
n } uma sua sele¸cão. Chama-se soma de Riemann
de f associada à parti¸cão P e sele¸cão C à seguinte soma,
Sf (P, C) :=
n
i=1
f (x∗
i )(xi − xi−1) .
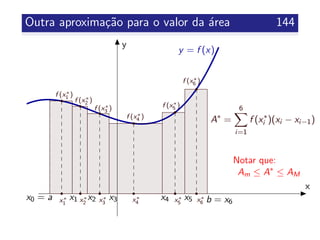
Obs 6.3
Nos slides anteriores, as somas Am, AM e A∗ são somas de
Riemann de f para uma mesma parti¸cão de [a, b] em 6
sub-intervalos, para três sele¸cões diferentes.

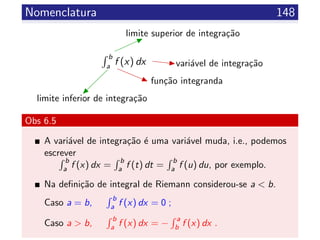
Integral de Riemann 147
Def 6.4
Sejam f : [a, b] → R e I ∈ R. Diz-se que I é o integral de Riemann
(ou integral definido) de f em [a, b] (ou de a para b) se
para todo o > 0 existe δ > 0 tal que, para toda a parti¸cão P de
[a, b], tal que ∆P < δ, se tem
|Sf (P, C) − I| <
para toda a sele¸cão C de P.
Caso exista I, nas condi¸cões anteriores, diz-se que f é integrável
em [a, b] e escreve-se
I =
b
a
f (x) dx .

Nomenclatura 148
b
a
f (x) dx
limite superior de integra¸cão
limite inferior de integra¸cão
variável de integra¸cão
fun¸cão integranda
Obs 6.5
A variável de integra¸cão é uma variável muda, i.e., podemos
escrever
b
a f (x) dx =
b
a f (t) dt =
b
a f (u) du, por exemplo.
Na defini¸cão de integral de Riemann considerou-se a < b.
Caso a = b,
b
a f (x) dx = 0 ;
Caso a > b,
b
a f (x) dx = −
a
b f (x) dx .

Integral de Riemann - caracteriza¸cão 149
Prop 6.6
Sejam f : [a, b] → R e I um número real.
Então I é o integral de Riemann de f de a para b se e só se, para
toda a sucessão (Pn)n∈N de parti¸cões do intervalo [a, b] tal que
lim
n→+∞
(∆Pn) = 0
se tem
lim
n→+∞
Sf (Pn, Cn) = I ,
para toda a sucessão (Cn)n∈N tal que, para cada n ∈ N, Cn é uma
sele¸cão de Pn.

Exerc´ıcios 150
Exe 6.7
1 Sabendo que f definida por f (x) = x é integrável em [0, 1],
mostre usando a proposi¸cão anterior que
1
0
x dx =
1
2
2 Seja k ∈ R. Sabendo que f definida por f (x) = k é integrável
no intervalo [a, b], mostre usando a proposi¸cão anterior que
b
a
k dx = k(b − a)

Carateriza¸cão das fun¸cões integráveis 151
Prop 6.8
Seja f uma f.r.v.r definida em [a, b]. Então f é integrável em [a, b]
se e só se, para todo o > 0, existe uma parti¸cão
P = {x0, x1, · · · , xn} do intervalo [a, b] tal que, para todas as
sele¸cões C = {x∗
1 , x∗
2 , · · · , x∗
n } e C = {x1, x2, · · · , xn} de P, se tem
n
i=1
|f (x∗
i ) − f (xi )|(xi − xi−1) < .

Propriedades das fun¸cões integráveis 152
Prop 6.9
Sejam f e g fun¸cões integráveis em [a, b] e α ∈ R.
1 f + g é integrável em [a, b] e
b
a
(f (x) + g(x)) dx =
b
a
f (x) dx +
b
a
g(x) dx;
2 αf é integrável em [a, b] e
b
a
αf (x) dx = α
b
a
f (x) dx;
3 |f | é integrável em [a, b];
4 fg é integrável em [a, b];
5 f é integrável em qualquer sub-intervalo [c, d] de [a, b];
6 Se c ∈]a, b[, então f é integrável em [a, c] e em [c, b] e
b
a
f (x) dx =
c
a
f (x) dx +
b
c
f (x) dx ;

Propriedades das fun¸cões integráveis (cont.) 153
Prop 6.9 (cont.)
7 Se f (x) ≥ 0, para todo o x ∈ [a, b], então
b
a
f (x) dx ≥ 0;
8 Se f (x) ≤ g(x), para todo o x ∈ [a, b], então
b
a
f (x) dx ≤
b
a
g(x) dx
9 Se m ≤ f (x) ≤ M, para todo o x ∈ [a, b], onde m, M ∈ R,
então
m(b − a) ≤
b
a
f (x) dx ≤ M(b − a)
10
b
a
f (x) dx ≤
b
a
|f (x)| dx

Critérios de Integrabilidade 154
Prop 6.10
Seja f : [a, b] → R uma fun¸cão. Se f é integrável em [a, b] então f
é limitada em [a, b].
Obs 6.11
A proposi¸cão anterior, permite concluir que se f não for
limitada em [a, b] então f não é integrável em [a, b].
A proposi¸cão anterior é apenas necessária, isto é, existem
fun¸cões limitadas num intervalo que não são integráveis nesse
intervalo.

Exerc´ıcios 155
Exe 6.12
1 Mostre que a fun¸cão f definida por
f (x) =
1
x se x = 0
0 se x = 0
não é integrável em qualquer intervalo fechado e limitado que
contenha a origem.
2 Verifique que a fun¸cão definida por
h(x) =
0 se x ∈ Q
1 se x ∈ R Q
é limitada mas não é integrável em [0, 1].

Condi¸cões de integrabilidade 156
Prop 6.13
Seja f : [a, b] → R uma fun¸cão.
1 Se f for cont´ınua em [a, b] então f é integrável em [a, b].
2 Se f for limitada em [a, b] e descont´ınua num número finito
de pontos então f é integrável em [a, b].
3 Se f for monótona em [a, b] então f é integrável em [a, b].
Prop 6.14
Sejam f e g fun¸cões definidas em [a, b]. Se f é integrável em [a, b]
e g difere de f apenas num número finito de pontos, isto é,
f (x) = g(x), para todo o x ∈ [a, b], exceto para um número finito
de x, então
g é integrável em [a, b] e
b
a
g(x) dx =
b
a
f (x) dx .

Exerc´ıcios 157
Exe 6.15
Diga, justificando, se as seguintes fun¸cões são integráveis no
intervalo considerado:
1 f (x) = cos(x2 − 2x), em [0, 4]
2 f (x) =
tg x se x ∈ 0, π
2
2 se x = π
2
, em 0, π
2
3 f (x) =



x + 1 se x ∈ [−2, 0[
2 se x = 0
x se x ∈]0, 1]
, em [−2, 1]
4 f (x) =
x + 1 se x ∈ [3, 7] e x ∈ N
1 se x ∈ [3, 7] ∩ N
, em [3, 7]

Teorema Fundamental de Cálculo Integral 158
Teo 6.16
Seja f uma fun¸cão integrável em [a, b] e F a fun¸cão definida em
[a, b] do modo seguinte
F(x) =
x
a
f (t) dt.
Então
(i) F é cont´ınua em [a, b];
(ii) se f é cont´ınua em c ∈]a, b[, então F é diferenciável
em c e F (c) = f (c).

Corolário do Teorema Fundamental 159
Obs 6.17
Uma vez que também é poss´ıvel mostrar que
1 se f é cont´ınua à direita em a, então existe F+(a) e tem-se
F+(a) = f (a);
2 se f é cont´ınua à esquerda em b, então existe F−(b) e tem-se
F−(b) = f (b).
do Teorema Fundamental do Cálculo Integral temos o seguinte
corolário que diz que toda a fun¸cão cont´ınua é primitivável.
Cor 6.18
Se f é cont´ınua em [a, b], então F(x) =
x
a f (t)dt, x ∈ [a, b], é
uma primitiva de f em [a, b].

Teorema do Valor Médio para Integrais 160
Cor 6.19
Seja f uma fun¸cão cont´ınua num intervalo [a, b].
Então existe c ∈]a, b[ tal que
b
a
f (t) dt = f (c)(b − a) .
Exe 6.20
Seja f (x) = x2 e F(x) =
x
1
f (t)dt.
1 Justifique que a fun¸cão F é cont´ınua em [1, 4].
2 Calcule F(1) e F (2).
3 Mostre que existe um c ∈]1, 4[ tal que F(4) = 3c2.

Deriva¸cão de integrais 161
Cor 6.21
Sejam I um intervalo aberto de R e [a, b] um intervalo de R.
Sejam f : [a, b] → R uma fun¸cão cont´ınua em ]a, b[ e g1 : I → R e
g2 : I → R duas fun¸cões diferenciáveis em I tais que g1(I) ⊂]a, b[ e
g2(I) ⊂]a, b[.
Então a fun¸cão H definida por
H(x) =
g2(x)
g1(x)
f (t) dt , para todo o x ∈ I ,
é diferenciável em I e, para todo o x ∈ I,
H (x) = f g2(x) g2(x) − f g1(x) g1(x) .

Exerc´ıcios 162
Exe 6.22
1 Calcule F (x) sendo F a f.r.v.r. dada por
(a) F(x)=
x
1
sen t2
+e−t2
dt
(b) F(x)=
2
x
cos t4
dt
(c) F(x)=
x3
cos x
ln(t2
+ 1) dt
(d) F(x)= x3
x
1
e−t2
dt
2 Seja F(x) =
x2
0
sen t2
dt. Calcule F 4 π
4 .
3 Considere a fun¸cão F definida em R por
F(x) =
x2
0
(4 + sen t) dt
(a) Calcule F (x) para todo o x ∈ R.
(b) Estude a fun¸cão F quanto à monotonia e existência de
extremos locais.

Exerc´ıcios 163
Exe 6.23
1 Considere a fun¸cão F definida em R por F(x) =
x3
0
tesen t
dt
(a) Justifique que F é diferenciável em R e determine F (x).
(b) Calcule lim
x→0
F(x)
sen x
2 Seja f : R → R um fun¸cão cont´ınua. Considere a fun¸cão ϕ
dada por
ϕ(x) =
1+x2
ex
f (t) dt, x ∈ R.
(a) Justifique que ϕ é diferenciável em R e determine ϕ (x).
(b) Mostre que lim
x→0
ϕ(x)
x
= −f (1).

Fórmula de Barrow 164
Prop 6.24
Se f : [a, b] → R é cont´ınua em [a, b] e se F : [a, b] → R é uma
primitiva de f então
b
a
f (x) dx = F(b) − F(a) .
Nota¸cão:
F(b) − F(a) = F(x)
b
a
= F(x)
b
a
Exe 6.25
1
2
1
(x2
− 1) dx =
x3
3
− x
2
1
=
8
3
− 2 −
1
3
− 1 =
4
3
2
e2
e
1
y ln y
dy = ln|ln y|
e2
e
= ln|ln(e2
)| − ln|ln(e)| = ln(2)

Exerc´ıcios 165
Exe 6.26
1 Calcule
(a)
1
0
2x
x2 + 1
dx
(b)
0
−π
sen(3x) dx
(c)
1
2
0
1
√
1 − x2
dx
(d)
11
3
1
√
2x + 3
dx
(e)
e2
e
1
x(ln x)2
dx
(f)
2
1
1
x2 + 2x + 5
dx
2 Calcule
1
−1
f (x) dx onde f (x)=



2
1 + x2
se x ∈[−1, 0[
7 se x = 0
1
1 + x
se x ∈]0, 1]

Integra¸cão por partes no integral definido 166
Prop 6.27
b
a
u v dx = uv
b
a
−
b
a
uv dx.
Exemplo de aplica¸cão:
π
0
x cos x dx = sen x . x
π
0
−
π
0
sen x dx
= 0 − − cos x
π
0
= cos π − cos 0
= −2
Exe 6.28
Calcule: (a)
1
2
0
(x + 1)e2x
dx (b)
e
1
x ln x dx

Mudan¸ca de variável no integral definido 167
Prop 6.29
Sejam f uma fun¸cão cont´ınua em I e
ϕ : J −→ I
t → x = ϕ(t)
diferenciável em J e tal que ϕ é cont´ınua em J.
Sejam a, b ∈ I e c, d ∈ J tais que ϕ(c) = a e ϕ(d) = b. Então
b
a
f (x) dx =
d
c
f (ϕ(t))ϕ (t) dt.
Obs 6.30
I e J denotam intervalos não degenerados de R
Exe 6.31
Calcule: (a)
ln 2
− ln 2
1
ex + 4
dx (b)
1
0
4 − x2 dx

Aplica¸cão ao cálculo de áreas 168
Prop 6.32
Se f é uma fun¸cão cont´ınua em [a, b] tal que f (x) ≥ 0, para todo
o x ∈ [a, b], então a área da região plana delimitada pelo gráfico
de f e pelas retas y = 0, x = a e x = b é dada por
b
a
f (x) dx
Ilustra¸cão gráfica
y = f (x)
A
ba
A =
b
a
f (x) dx

Aplica¸cão ao cálculo de áreas (cont.) 169
Prop 6.33
Se f é uma fun¸cão cont´ınua em [a, b] tal que f (x) ≤ 0, para todo
o x ∈ [a, b], então a área da região plana delimitada pelo gráfico
de f e pelas retas y = 0, x = a e x = b é dada por
−
b
a
f (x) dx
x
y
y = f (x)
A
ba
A = −
b
a
f (x) dx

Aplica¸cão ao cálculo de áreas (cont.) 170
Prop 6.34
Se f e g são fun¸cões cont´ınuas em [a, b] tais que f (x) ≥ g(x),
para todo o x ∈ [a, b], então a área da região plana delimitada
pelos gráficos de f e de g e pelas retas x = a e x = b é dada por
b
a
(f (x) − g(x)) dx
A =
b
a
(f (x) − g(x)) dx

Exerc´ıcios 171
Exe 6.35
1 Calcule a área da região delimitada pelos gráficos das fun¸cões
f (x) = 1
x e g(x) = x2 e pelas retas x = 2 e y = 0.
2 Seja f (x) = x3 − 3x2 + 2x. Calcule a área da região limitada
do plano situada entre as retas de equa¸cão x = 0 e x = 2 e
limitada pelo gráfico de f e pelo eixo Ox.
3 Calcule a área da região do plano situada entre x = −1
2 e
x = 0 e limitada pelo eixo das abcissas e pelo gráfico da
fun¸cão h definida por
h(x) =
arcsen x
√
1 − x2
4 Seja A = {(x, y) ∈ R2 : y ≥ (x − 3)2, y ≥ x − 1, y ≤ 4}.
(a) Represente geometricamente a região A.
(b) Calcule o valor da área da região A.

C´alculo I 172
Integrais impr´oprios
Ricardo Pereira
Dezembro de 2012

Integrais Impróprios 173
Obs 7.1
A defini¸cão de integral de Riemann exige que a fun¸cão integranda,
f , esteja definida num intervalo fechado e limitado, I, e que f seja
limitada. Vamos agora estender este conceito omitindo uma (ou as
duas) dessas condi¸cões, passando ao estudo do que chamamos
Integrais Impróprios.
Os Integrais Impróprios podem ser de três espécies:
1.a Espécie: I é ilimitado
2.a Espécie: f é ilimitada ou não definida em alguns pontos de I
3.a Espécie: I é ilimitado e f é ilimitada ou não definida em
alguns pontos de I

Integrais Impróprios de 1.a
Espécie 174
Def 7.2
Integral impróprio de 1.a espécie no limite superior de integra¸cão
Seja f : [a, +∞[→ R uma fun¸cão integrável em [a, t], para todo o
t ≥ a. Se existe e é finito o limite
lim
t→+∞
t
a
f (x) dx
então o integral impróprio
+∞
a
f (x) dx diz-se convergente e
escreve-se
+∞
a
f (x) dx = lim
t→+∞
t
a
f (x) dx.
Caso contrário, o integral em causa diz-se divergente.

Exemplo 175
Exe 7.3
Como
lim
t→+∞
t
0
1
1 + x2
dx = lim
t→+∞
[arctg(x)]t
0
= lim
t→+∞
arctg t
=
π
2
,
o integral impr´oprio
+∞
0
1
1 + x2
dx ´e convergente e
+∞
0
1
1 + x2
dx =
π
2
.

Exerc´ıcios 176
Exe 7.4
1 Determine a natureza dos seguintes integrais impróprios e, em
caso de convergência, calcule o seu valor:
(a)
+∞
π
cos(x)dx (b)
+∞
2
1
(x + 2)2
dx (c)
+∞
1
(ln x)3
x
dx
2 Prove que o integral impróprio
+∞
1
1
xα
dx é:
divergente se α ≤ 1;
convergente se α > 1 e, neste caso,
+∞
1
1
xα
dx =
1
α − 1
.
+∞
0
eβx
dx é:
divergente se β ≥ 0;
convergente se β < 0 e, neste caso,
+∞
0
eβx
dx = −
1
β
.

Espécie (cont.) 177
Def 7.5
Integral impróprio de 1.a espécie no limite inferior de integra¸cão
Seja f : ] − ∞, a] → R uma fun¸cão integrável em [t, a], para todo o
t ≤ a. Se existe e é finito o limite
lim
t→−∞
a
t
f (x) dx
a
−∞
escreve-se
a
−∞
f (x) dx = lim
t→−∞
a
t
f (x) dx.
Caso contrário, o integral em causa diz-se divergente.

Exemplo 178
Exe 7.6
Como
lim
t→−∞
1
t
1
1 + x2
dx = lim
t→−∞
[arctg(x)]1
t
= lim
t→−∞
(
π
4
− arctg t)
=
3π
4
,
o integral impr´oprio
1
−∞
1
1 + x2
dx ´e convergente e
1
−∞
1
1 + x2
dx =
3π
4
.

Exerc´ıcios 179
Exe 7.7
1 Determine a natureza dos seguintes integrais impróprios e, em
caso de convergência, calcule o seu valor:
(a)
0
−∞
xe−x2
dx
(b)
2
−∞
1
4 − x
dx
(c)
0
−∞
4
1 + (x + 1)2
dx
2 Estude a natureza do seguinte integral impróprio em fun¸cão
do parâmetro a ∈ R+ {1}
0
−∞
ax
dx

Propriedades dos integrais impróprios 180
Prop 7.8
Sejam f : [a, +∞[→ R e g : [a, +∞[→ R fun¸cões integráveis em
[a, t], ∀t ≥ a. Então verificam-se as seguintes condi¸cões:
1 Se
+∞
a
f (x) dx e
+∞
a
g(x) dx são convergentes, então
+∞
a
(αf (x) + βg(x)) dx é convergente, ∀α, β ∈ R, e
+∞
a
(αf (x)+βg(x)) dx = α
+∞
a
f (x) dx +β
+∞
a
g(x) dx.
2 Se
+∞
a
f (x) dx é divergente, então
+∞
a
(αf (x)) dx é
divergente, para todo o α ∈ R {0}.
Obs 7.9
Resultado análogo é válido para integrais impróprios de 1.a espécie
no limite inferior de integra¸cão.

Propriedades dos integrais impróprios (cont.) 181
Prop 7.10
Sejam f : [a, +∞[→ R uma fun¸cão integrável em [a, t], para todo
o t ≥ a, e b > a. Então os integrais impróprios
+∞
a
f (x) dx e
+∞
b
f (x) dx
têm a mesma natureza (i.e., ou são ambos convergentes ou ambos
divergentes). Em caso de convergência, tem-se que
+∞
a
f (x) dx =
b
a
f (x) dx +
+∞
b
f (x) dx.
Obs 7.11
Resultado análogo, com as devidas adapta¸cões, é válido para
integrais impróprios de 1.a espécie no limite inferior de integra¸cão.

Exemplos 182
Exe 7.12
1 Pelo Exerc´ıcio 7.4.2 tem-se que
+∞
1
1
x3
dx converge e que
+∞
1
1
x3
dx =
1
2
.
Portanto
+∞
1
2
1
x3
dx =
1
1
2
1
x3
dx +
+∞
1
1
x3
dx =
3
2
+
1
2
= 2.
2 Como, atendendo ao Exerc´ıcio 7.4.2, o integral impróprio
+∞
1
x2
dx é divergente, então o integral impróprio
+∞
3
x2
dx também é divergente.

Def 7.13
Integral impróprio de 1.o espécie em ambos os limites de integra¸cão
Seja f : R → R uma fun¸cão integrável em [α, β] para todos os
α, β ∈ R tais que α < β.
1 Se, para algum a ∈ R, os integrais impróprios
a
−∞
f (x) dx e
+∞
a
f (x) dx são ambos convergentes
dizemos que o integral impróprio
+∞
−∞
f (x) dx é convergente
e escrevemos
+∞
−∞
f (x) dx =
a
−∞
f (x) dx +
+∞
a
f (x) dx .

Def 7.14 (cont.)
2 Se, para algum a ∈ R, pelo menos um dos integrais impróprios
a
−∞
f (x) dx ou
+∞
a
f (x) dx
é divergente dizemos que o integral impróprio
+∞
−∞
f (x) dx é
divergente.
Exe 7.15
Determine a natureza dos seguintes integrais impróprios e, em caso
de convergência, calcule o seu valor:
(a)
+∞
−∞
x dx (b)
+∞
−∞
1
1 + x2
dx (c)
+∞
−∞
2x
dx

Critério de Compara¸cão 185
Prop 7.16
Sejam f e g duas fun¸cões definidas em [a, +∞[, integráveis em
[a, t], para todo o t ≥ a, tais que
0 ≤ f (x) ≤ g(x) ,
para todo o x ∈ [a, +∞[. Então:
(i) se
+∞
a
g(x) dx é convergente, então
+∞
a
(ii) se
+∞
a
+∞
a
g(x) dx é divergente.
Obs 7.17
Com ligeiras adapta¸cões, pode enunciar-se o mesmo critério para
integrais impróprios de 1.a espécie, impróprios no limite inferior de
integra¸cão.

Exemplo 186
Exe 7.18
Usando o Critério de Compara¸cão estudar a natureza do integral
+∞
1
sen
1
x2
dx .
Notar que, para todo o x ∈ [1, +∞[ temos
0 ≤ sen
1
x2
≤
1
x2
. (justifique!) (1)
Uma vez que o integral impróprio
+∞
1
1
x2
dx é convergente e que
a desigualdade (1) se verifica, pelo Critério de Compara¸cão, o
integral impróprio
+∞
1
sen
1
x2
dx é convergente.

Critério do Limite 187
Prop 7.19
Sejam f e g duas fun¸cões definidas em [a, +∞[ e integráveis em
[a, t], ∀t ≥ a, tais que f (x) ≥ 0 e g(x) > 0, ∀x ∈ [a, +∞[. Seja
L = lim
x→+∞
f (x)
g(x)
.
Então:
(i) Se L ∈ R+, então
+∞
a
f (x) dx e
+∞
a
g(x) dx têm a
mesma natureza.
(ii) Se L = 0 e
+∞
a
+∞
a
f (x) dx
é convergente.
(iii) Se L = +∞ e
+∞
a
g(x) dx é divergente, então
+∞
a
f (x) dx
é divergente.

Exemplo 188
Exe 7.20
Usando o Critério do Limite estudar a natureza do integral
+∞
1
sen
1
x2
dx .
Notar que, ∀x ∈ [1, +∞[, sen 1
x2 ≥ 0 e 1
x2 > 0. Além disso
L = lim
x→+∞
sen 1
x2
1
x2
= 1 .
Uma vez que L ∈ R+ e que
+∞
1
1
x2
dx é convergente, pelo
Critério do Limite, o integral impróprio
+∞
1
sen
1
x2
dx é
convergente.

Critérios de Convergência (cont.) 189
Obs 7.21
Tanto o Critério de Compara¸cão como o Critério do Limite têm as
suas versões para integrais impróprios de 1.a espécie, impróprios no
limite de integra¸cão inferior, basta fazer pequenas adapta¸cões nos
enunciados apresentados nos slides anteriores.
Exe 7.22
Estudo da natureza do integral impróprio
0
−∞
ex
(x − 1)2
dx.
∀x ∈] − ∞, 0], ex
(x−1)2 > 0 e 1
(x−1)2 > 0 .
Uma vez que
L = lim
x→−∞
ex
(x−1)2
1
(x−1)2
= lim
x→−∞
ex
= 0
e que
0
−∞
1
(x − 1)2
dx é convergente (verifique!), conclu´ımos,
pelo Critério do Limite, que
0
−∞
ex
(x − 1)2
dx é convergente.

Exerc´ıcios 190
Exe 7.23
Estude, utilizando o critério de compara¸cão ou critério do limite, a
natureza dos seguintes integrais impróprios:
(a)
+∞
1
sen2 x
x
5
2
dx
(b)
+∞
1
5x2 − 3
x8 + x − 1
dx
(c)
+∞
0
ex2
dx
(d)
+∞
1
x
ex − 1
dx

Convergência absoluta 191
Def 7.24
Seja f : [a, +∞[→ R integrável em [a, t], para todo o t ∈ [a, +∞[.
Dizemos que o integral impróprio
+∞
a
f (x) dx
é absolutamente convergente, se o integral impróprio
+∞
a
|f (x)| dx
é também convergente.
Prop 7.25
Seja f : [a, +∞[→ R integrável em [a, t], para todo o t ∈ [a, +∞[.
Se o integral impróprio
+∞
a
f (x) dx
é absolutamente convergente, então também é convergente.

Exerc´ıcios 192
Obs 7.26
Com ligeiras adapta¸cões, pode definir-se convergência absoluta e
enunciar-se a mesma proposi¸cão para integrais impróprios de 1.a
espécie, impróprios no limite inferior de integra¸cão.
Exe 7.27
Verifique se os seguintes integrais impróprios são absolutamente
convergentes:
(a)
+∞
1
sen x
x2
dx
(b)
+∞
2
(−1)n
1 + 2x4
dx, para todo o n ∈ N

Espécie 193
Def 7.28
Integral impróprio de 2.a espécie no limite de integra¸cão inferior
Seja f : ]a, b] → R uma fun¸cão integrável em [t, b], para todo o
a < t ≤ b. Se existe e é finito
lim
t→a+
b
t
f (x) dx
b
a
f (x) dx é convergente e
escrevemos, por defini¸cão,
b
a
f (x) dx = lim
t→a+
b
t
f (x) dx .
Caso contrário, dizemos que o integral impróprio é divergente.

Def 7.29
Integral impróprio de 2.a espécie no limite de integra¸cão superior
Seja f : [a, b[→ R uma fun¸cão integrável em [a, t], para todo o
a < t ≤ b. Se existe e é finito
lim
t→b−
t
a
f (x) dx
b
a
f (x) dx é convergente e
escrevemos, por defini¸cão,
b
a
f (x) dx = lim
t→b−
t
a
f (x) dx .

Def 7.30
Integral impróprio de 2.a espécie em ambos os limites de integra¸cão
Seja f : ]a, b[→ R uma fun¸cão integrável em [t1, t2], para todos os
t1 e t2 tais que a < t1 < t2 < b.
b
a
f (x) dx é convergente se,
para algum c ∈]a, b[, os integrais
c
a
f (x) dx e
b
c
f (x) dx
são ambos convergentes e escreve-se
b
a
f (x) dx =
c
a
f (x) dx +
b
c
f (x) dx .

Def 7.31
Integral impróprio de 2.a espécie num ponto interior do intervalo de
integra¸cão
Seja f uma fun¸cão definida em [a, b] exceto possivelmente em
c ∈]a, b[, e integrável em [a, t], para todo o a ≤ t < c e em [r, b],
para todo o c < r ≤ b. Se os integrais impróprios
c
a
f (x) dx e
b
c
f (x) dx forem ambos convergentes,
b
a
escreve-se
b
a
f (x) dx =
c
a
f (x) dx +
b
c
f (x) dx .

Exerc´ıcios 197
Exe 7.32
Determine a natureza dos seguintes integrais impr´oprios e, em caso
de convergˆencia, calcule o seu valor:
(a)
1
0
1
√
1 − x2
dx
(b)
π
2
0
cos x
1 − sen x
dx
(c)
3
−3
x
√
9 − x2
dx
(d)
1
−2
1
|x|
dx
(e)
3
0
1
(x − 1)(x − 2)
dx

Observa¸cão 198
Obs 7.33
As propriedades, defini¸cões e critérios de convergência apresentados
para o integral de 1.a espécie têm as suas versões para os integrais
de 2.a espécie (no limite inferior de integra¸cão ou no limite superior
de integra¸cão). Nos slides seguintes apresentamos esses resultados
para o caso dos integrais de 2.a espécie no limite inferior de
integra¸cão, para os outros o estudo faz-se mutatis mutandis.

Propriedades dos integrais impróprios 199
Prop 7.34
Sejam f :]a, b] → R e g :]a, b] → R fun¸cões integráveis em [t, b],
para todo o t ∈]a, b]. Então verificam-se as seguintes condi¸cões:
1 Se
b
a
f (x) dx e
b
a
g(x) dx são convergentes, então
b
a
(αf (x) + βg(x)) dx é convergente, ∀α, β ∈ R, e
b
a
(αf (x) + βg(x)) dx = α
b
a
f (x) dx + β
b
a
g(x) dx .
2 Se
b
a
b
a
(αf (x)) dx é
divergente, para todo o α ∈ R {0}.

Propriedades dos integrais impróprios (cont.) 200
Prop 7.35
Sejam f : ]a, b] → R uma fun¸cão integrável em [t, b], para todo o
t ∈]a, b], e a < b < b. Então os integrais impróprios
b
a
f (x) dx e
b
a
f (x) dx
têm a mesma natureza (i.e., ou são ambos convergentes ou ambos
divergentes). Em caso de convergência, tem-se que
b
a
f (x) dx =
b
a
f (x) dx +
b
b
f (x) dx.

Critério de Compara¸cão 201
Prop 7.36
Sejam f e g duas fun¸cões definidas em ]a, b], integráveis em [t, b],
para todo o t ∈]a, b], tais que
0 ≤ f (x) ≤ g(x) ,
para todo o x ∈]a, b]. Então:
(i) se
b
a
b
a
(ii) se
b
a
b
a
g(x) dx é divergente.

Critério do Limite 202
Prop 7.37
Sejam f e g duas fun¸cões definidas em ]a, b] e integráveis em
[t, b], ∀t ∈]a, b], tais que f (x) ≥ 0 e g(x) > 0, ∀x ∈]a, b]. Seja
L = lim
x→a+
f (x)
g(x)
.
Então:
(i) Se L ∈ R+, então
b
a
f (x) dx e
b
a
g(x) dx têm a mesma
natureza.
(ii) Se L = 0 e
b
a
b
a
f (x) dx é
convergente.
(iii) Se L = +∞ e
b
a
g(x) dx é divergente, então
b
a
f (x) dx é
divergente.

Convergência absoluta 203
Def 7.38
Seja f : ]a, b] → R integrável em [t, b], para todo o t ∈]a, b].
b
a
f (x) dx é absolutamente convergente,
se o integral impróprio
b
a
|f (x)| dx é também convergente.
Prop 7.39
Seja f : ]a, b] → R integrável em [t, b], para todo o t ∈]a, b].
Se o integral impróprio
b
a
f (x) dx
é absolutamente convergente, então também é convergente.

Exerc´ıcios 204
Exe 7.40
1
0
1
xα
dx ´e:
divergente se α ≥ 1;
convergente se α < 1 e, neste caso,
1
0
1
xα
dx =
1
1 − α
.
2 Estude a natureza dos seguintes integrais impr´oprios:
(a)
1
0
π
1 −
√
x
dx
(b)
π
2
0
sen
√
x
4
√
x
dx

Espécie 205
Def 7.41
Integral impróprio de 3.a espécie do tipo
+∞
a
f (x) dx,
onde f é ilimitada ou não está definida em x = a.
Seja f : ]a, +∞[→ R integrável em [t, t ], quaisquer que sejam
t, t ∈ R tais que a < t < t .
+∞
a
para algum c ∈]a, +∞[, os integrais impróprios
c
a f (x) dx e
+∞
c f (x) dx forem ambos convergentes e escrevemos
+∞
a
f (x) dx =
c
a
f (x) dx +
+∞
c
f (x) dx

Def 7.42
Integral impróprio de 3.a espécie do tipo
b
−∞
f (x) dx,
onde f é ilimitada ou não está definida em x = b.
Seja f : ] − ∞, b[→ R integrável em [t, t ], quaisquer que sejam
t, t ∈ R tais que t < t < b.
b
−∞
para algum c ∈] − ∞, b[, os integrais impróprios
c
−∞ f (x) dx e
b
c f (x) dx forem ambos convergentes e escrevemos
b
∞
f (x) dx =
c
−∞
f (x) dx +
b
c
f (x) dx

Obs 7.43
Definem-se de modo análogo os integrais impróprios de 3.a
espécie dos tipos
+∞
a
f (x) dx,
b
−∞
f (x) dx e
+∞
−∞
f (x) dx,
onde f não está definida ou é ilimitada em algum ponto do
interior do intervalo de integra¸cão.
Atendendo às defini¸cões apresentadas, para estudar a natureza
de integrais impróprios de 3.a espécie, devemos decompor o
intervalo de integra¸cão de modo conveniente e estudar a
natureza de integrais impróprios de 1.a e de 2.a espécies
(correspondentes).

Exerc´ıcios 208
Exe 7.44
1 Estude a natureza dos seguintes integrais impr´oprios:
(a)
+∞
0
e−
√
x
√
x
dx
(b)
+∞
−∞
1
x3
dx
2 Calcule
+∞
−∞
f (x) dx sendo
f (x) =



1
x−1 se x ≤ 0
arctg x se x > 0

Cálculo I engenharias

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Cálculo I engenharias

Cálculo I engenharias