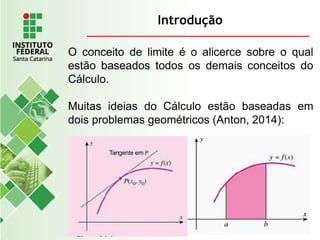
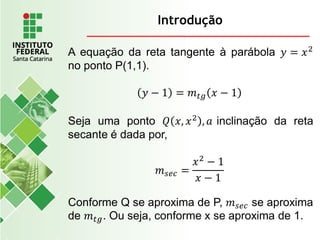
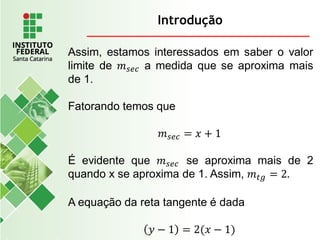
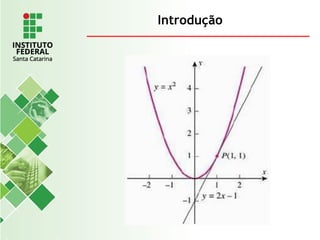
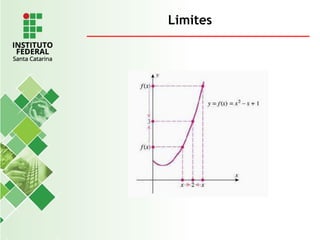
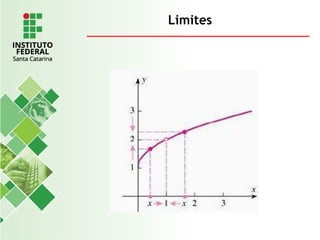
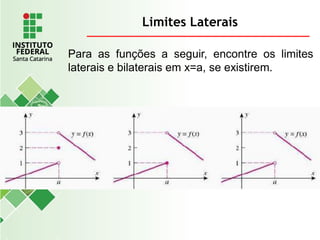
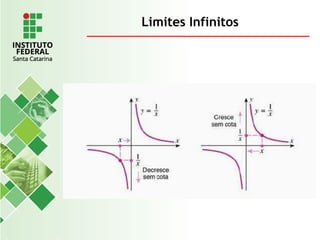
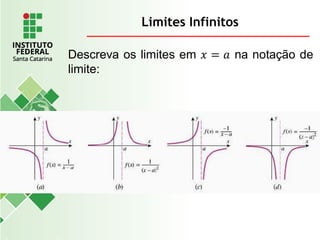
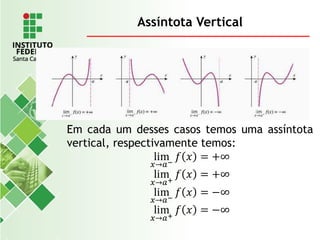
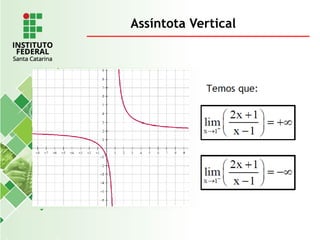
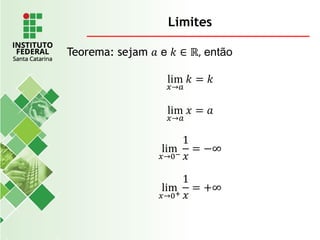
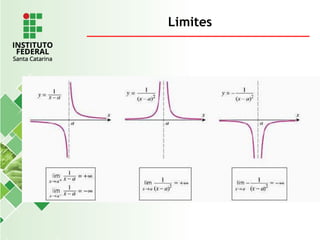
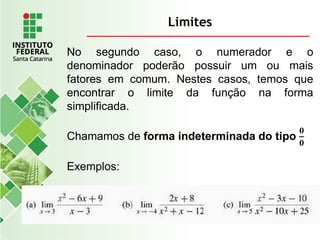
O documento explora o conceito de limite, fundamental no cálculo, utilizando exemplos geométricos e analíticos para ilustrar seu comportamento próximo a valores específicos. Ele discute limites laterais, bilaterais e infinitos, detalhando como determiná-los e as implicações de assíntotas verticais. Além disso, aborda propriedades de limites com funções racionais e casos indeterminados como 0/0.