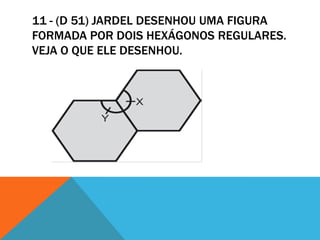
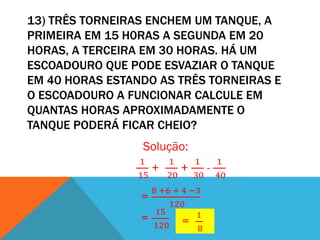
O documento apresenta 13 problemas matemáticos com suas respectivas soluções. Os problemas envolvem conceitos como progressão aritmética e geométrica, porcentagem, juros compostos, relação entre grandezas e misturas. As soluções utilizam cálculos, fórmulas e raciocínios lógicos para chegar aos resultados corretos.

1. E.E.E.P. DEP. JOSÉ MARIA MELO
Professor: F.E.M

2. SENSAÇÃO ESTUDAR MATEMÁTICA

3. 1 - (D41) O NÚMERO DE MÚLTIPLOS DE 5
COMPREENDIDOS ENTRE 21 E 623 É.
A) 60 Solução:
B) 61 an = a1 + (n – 1)r
C) 120 a1 = 25
r=5
D) 1 21
an = 620
E) 122
Como procuramos n que é o numero
de termos dessa P.A, então:
620 = 25 + (n – 1) 5
620 – 25 = 5n – 5
595 + 5 = 5n
n = 120

4. Fórmulas relacionadas
Soma de N termos de uma P.A:
(a1 + an)n
Sn =
2
Termo geral de uma P.G
an = a1 qn-1
Soma de N termos de uma P.G Finita:
_
n 1
a1q
Sn =
𝑞−1
Soma de N termos de uma P.G Infinita:
a1
Sn =
1−𝑞

5. Mas como isso funciona?

6. DESAFIO:
A MEDIDA DO LADO DE UM TRIÂNGULO
EQUILÁTERO É 4 CM. UNINDO-SE OS PONTOS
MÉDIOS DE SEUS LADOS OBTÉM-SE UM NOVO
TRIÂNGULO EQUILÁTERO. REPETE-SE ESSE
PROCESSO SUCESSIVA E INFINITAMENTE COMO
NA FIGURA.
QUAL A SOMA DOS PERÍMETROS DE TODOS
ESSES TRIÂNGULOS?

7. 2 - (D18) LEONARDO LEVA 12 MINUTOS PARA
MONTAR UM QUEBRA CABEÇA DE 60 PEÇAS.
EM QUANTO TEMPO ELE MONTA UM QUEBRA
CABEÇA DE 180 PEÇAS?
A) 3 min Solução:
B) 4 min 12mim 60 peç
C) 5 min x 180peç
D) 15 min
60x = 12 . 180
E) 36 min X = 36

8. Desafio:
UMA EQUIPE DE 20 OPERÁRIOS ESCAVA 640 M
3 DE TERRA EM 8H DE TRABALHO. PARA
ESCAVAR 500 M 3 EM 5H DE TRABALHO, DE
QUANTOS OPERÁRIOS DEVERÁ SER ACRESCIDA
A EQUIPE?

9. 3 - (D32) PARA IRRIGAR UMA PLANTAÇÃO DE
TOMATES UTILIZAM-SE JATOS DE ÁGUA EM
FORMA DE PARÁBOLAS. A FUNÇÃO H(T)= -T² +
2T + 3 REPRESENTA A ALTURA EM METROS.
QUAL A ALTURA MÁXIMA ATINGIDA POR ESSES
JATOS?
A) 1 Solução:
Como procuramos a altura MÁXIMA
B) 2 logo procuramos o vértice da
C) 3 parábola dado por:
D) 4 ∆ 𝑏
yv = - xv = -
4𝑎 2𝑎
E) 6
∆ = b² − 4. 𝑎 . 𝑐

10. Substituindo na fórmula temos:
2²−4. −1 .3
yv = -
4.(−1)
16
yv = -
−4
yv = 4

11. 4 - (D39) UM FAZENDEIRO VENDEU NO 1º MÊS
12 VACAS, NO 2º MÊS 14 VACAS, NO 3º MÊS 16
VACAS, SEGUINDO ESSA MESMA PROPORÇÃO,
QUANTAS VACAS VENDEU AO FINAL DE UM ANO.
Solução:
A) 34
B) 46 1° 12 vacas
C) 276 2° 14vacas
D) 288 3° 16 vacas
E) 300 4° 18 vacas
5° 20 vacas
6° 22 vacas
7° 24 vacas

12. Soma total de todos os 8° 26 vacas
meses temos Sn = 12 + 9° 28 vacas
14 + ...32 + 34 10° 30 vacas
Sn = 276 11° 32 vacas
12° 34 vacas
Outra maneira de Fazer:
(a1 + an)n
an = a1 + (n – 1)r Sn =
2
an = ? 12 +34 12
n = 12 Sn =
2
r=2 Sn = 276
a12 = 12 + (12 – 1)2
a12 = 34

13. 5 - (D29) EM UMA CIDADE UM PEDREIRO
COBRA UMA TAXA FIXA DE R$ 32,00, MAIS R$
13,00 POR HORA TRABALHADA. QUANTO ELE
RECEBE SE TRABALHOU 8 HORAS?
Solução:
A) 104 Teremos uma função do 1° grau do tipo:
B) 136 s(h) = 32 + 13 h
C) 269 s(8) = 32 + 13 . 8
D) 360 s(8) = 136
E) 520

14. 6 - (D17) UM SUCO QUE CUSTAVA R$ 2,80, TEVE
UM AUMENTO DE 200%, PASSOU A CUSTAR:
A) R$ 3,36
Solução:
B) R$ 4,80
200 560
C) R$ 5,60 x 2,80 = = 5,60
100 100
D) R$ 8,40
Logo 200% de R$ 2,80 é o
mesmo que R$ 5,60
e como antes o suco custa R$
2,80 passou a custar 5,60 +
2,80 = 8,40

15. 7 - (D41) NUMA VIAGEM ALINE LEVOU EM SUA
MOCHILA, 2 CALÇAS, 1 SAIA E 4 BLUSAS. DE
QUANTAS MANEIRAS DIFERENTES ELA PODERÁ
SE VESTIR:
A) 7
B) 8
C) 9
D) 12
E) 13

16. DESAFIO...
A RAZÃO ENTRE AS MASSAS DE DOIS METAIS A
E B NA COMPOSIÇÃO DE UMA LIGA METÁLICA É
2:3. SE O VALOR DO GRAMA DE A É R$
8.000,00 E O DE B É R$ 6.000,00, ENTÃO O
VALOR DO GRAMA DA LIGA EM R$ É:

17. 08 - (D 44) O GRÁFICO MOSTRA A
TEMPERATURA NUMA CIDADE DA REGIÃO SUL,
EM UM DIA DO MÊS DE JULHO.

18. A TEMPERATURA AUMENTA NO PERÍODO DE
(A) 8 às 16h.
(B) 16 às 24h.
(C) 4 às 12h.
(D) 12 às 16h.
(E) 4 às 16h.

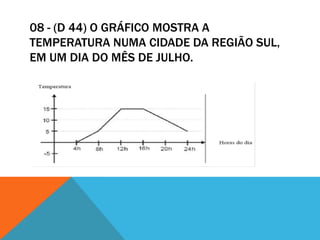
19. 9 - (D 44) CONSIDERE A FUNÇÃO Y = F(X), NO
INTERVALO [-6,6]

20. A FUNÇÃO Y = F (X) É CONSTANTE NO
INTERVALO:
(A) [0,4]
(B) [-1,0]
(C) [-1,2]
(D) [2,4]
(E) [4,6]

21. 10 - (D 46) AO PASSAR SUA MÃO DIREITA POR
TODOS OS VÉRTICES E ARESTAS DE UM
POLIEDRO, SOMENTE UMA VEZ, UM DEFICIENTE
VISUAL PERCEBE QUE PASSOU POR 8 VÉRTICES
E 12 ARESTAS. O NÚMERO DE FACES DESSE
POLIEDRO É, ENTÃO, IGUAL A
(A) 20.
(B) 12.
(C) 8.
(D) 6.
(E) 4.

22. 11 - (D 51) JARDEL DESENHOU UMA FIGURA
FORMADA POR DOIS HEXÁGONOS REGULARES.
VEJA O QUE ELE DESENHOU.

23. NESSA FIGURA, A SOMA DAS MEDIDAS DOS
ÂNGULOS X E Y É:
(A) 60º
(B) 120º
(C) 240º
(D) 360º
(E) 720º

24. 12 - (D39) MARIA JOGOU EM UM POÇO NA
SEGUNDA FEIRA 2 MOEDAS, NA TERÇA FEIRA 4
MOEDAS. QUAL O TOTAL DE MOEDAS NO
DOMINGO, SABENDO QUE A CADA DIA
AUMENTAVA O DOBRO.
A) 14 Solução:
B) 64 Segunda 2
C) 126 Terça 4
Quarta 8
D) 128
E) 254 Quinta 16
Sexta 32
Somando-se todos
os valores temos Sábado 64
Sn = 254 Domingo 128

25. 13) TRÊS TORNEIRAS ENCHEM UM TANQUE, A
PRIMEIRA EM 15 H0RAS A SEGUNDA EM 20
HORAS, A TERCEIRA EM 30 HORAS. HÁ UM
ESCOADOURO QUE PODE ESVAZIAR O TANQUE
EM 40 HORAS ESTANDO AS TRÊS TORNEIRAS E
O ESCOADOURO A FUNCIONAR CALCULE EM
QUANTAS HORAS APROXIMADAMENTE O
TANQUE PODERÁ FICAR CHEIO?
Solução:
1 1 1 1
+ + -
15 20 30 40
8 +6 + 4 −3
=
120
15 1
=
120 = 8

26. “GASTE ALGUM TEMPO
FAZENDO A COISA CERTA,
PARA NÃO GASTAR MUITO
TEMPO EXPLICANDO POR
QUE NÃO DEU CERTO.”