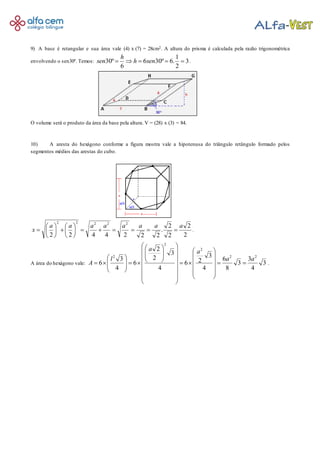
1) O documento apresenta resumos de problemas de matemática resolvidos, incluindo razões entre volumes e áreas de sólidos semelhantes, cálculo de volumes derramados e áreas de figuras geométricas. 2) Fornece a fórmula para calcular a razão entre volumes e áreas de sólidos semelhantes com base nas razões entre suas alturas. 3) Explica como calcular o volume derramado de um prisma através da aplicação de razões trigonométricas.

1. TD 13 - Matemática III – GABARITO
1)
2)
3) C
4)

2. 5) Como os sólidos são semelhantes, a razão entre seus volumes é igual ao cubo da razão entre suas alturas, e a razão
entre sua áreas é igual ao quadrado da razão entre suas alturas. Se o pacote maior tem volume V, área total AT e altura
H, e o menor tem volume v, área total at e altura h, então:
Portanto:
Como V = 2v, logo:
6) D
7)
8) O volume derramado é o volume da parte “vazia” indicada pelo prisma pintado.
A linha horizontal paralela à base estabelece um ângulo de 30º oposto à aresta “x”
do prisma.
Aplicando a razão trigonométrica da tangente, temos:
3
310
3
3
10
3
3
º30
10
º30









x
x
tg
x
tg
. A área da base é a área do triângulo
retângulo calculada pelo produto dos catetos. A altura do prisma coincide com a aresta que mede 7cm. Logo o volume
derramado é
3
3
3350
)7.()10.(
3
310
.
2
1
cmV 


















3. 9) A base é retangular e sua área vale (4) x (7) = 28cm2. A altura do prisma é calculada pela razão trigonométrica
envolvendo o sen30º. Temos: 3
2
1
.6º306
6
º30  senh
h
sen .
O volume será o produto da área da base pela altura. V = (28) x (3) = 84.
10) A aresta do hexágono conforme a figura mostra vale a hipotenusa do triângulo retângulo formado pelos
segmentos médios das arestas do cubo.
2
2
2
2
.
2224422
22222
aaaaaaaa
x 











 .
A área do hexágono vale: 3
4
3
3
8
6
4
3
26
4
3
2
2
6
4
3
6
22
2
2
2
aa
aa
l
A 











































 .