1. Os valores possíveis de m para que exista solução para a equação senx = m-2/2 são entre -2 e 2. 2. O valor de m deve estar entre 1/3 e 2/3 para que a equação cos2x = 3m - 1 tenha solução. 3. O conjunto imagem da função f(x) = 2senx - 2 é entre -4 e 0.

1. 1. Os valores que m pode assumir, para que exista o arco x satisfazendo a igualdade senx =
m−2
2
, são:
a) -1 ≤ m ≤1
b) 2 ≤ m ≤ 4
c) -4 ≤ m ≤ 4
d) 0 ≤ m ≤ 4
e) -2 ≤ m ≤ 2
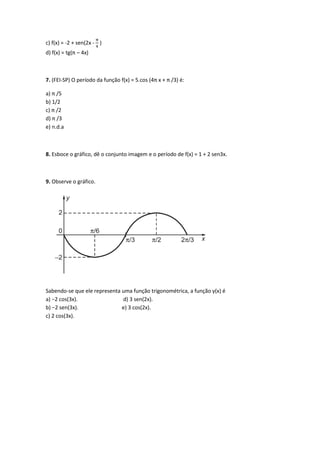
2. Determine m de modo que se verifique cos²x = 3m – 1.
3. (UFC-CE) O conjunto imagem da função f(x) = 2 senx – 2 é:
a) [-1, 1]
b) [-2, 2]
c) [-4, 0]
d) [-3, 3]
e) [-3, 0]
4. (UFPB) Qual é o maior valor da constante real k, para que a equação 3 senx + 13 = 4k possua
solução?
a) 5/2
b) 3
c) 7/2
d) 11/2
e) 4
5. (UEMT) O conjunto imagem da função y = 2 – 3 sen
x
2
é:
a) [-1, 1]
b) [-1, 3]
c) [-1, 5]
d) [1, 5]
e) [-5, 5]
6. Determinar o período das funções:
a) f(x) = sen3x
b) f(x) = cos(πx)

2. c) f(x) = -2 + sen(2x -
π
4
)
d) f(x) = tg(π – 4x)
7. (FEI-SP) O período da função f(x) = 5.cos (4π x + π /3) é:
a) π /5
b) 1/2
c) π /2
d) π /3
e) n.d.a
8. Esboce o gráfico, dê o conjunto imagem e o período de f(x) = 1 + 2 sen3x.
9. Observe o gráfico.
Sabendo-se que ele representa uma função trigonométrica, a função y(x) é
a) −2 cos(3x). d) 3 sen(2x).
b) −2 sen(3x). e) 3 cos(2x).
c) 2 cos(3x).

3. 10. (Ufrn 2001) A figura abaixo representa o gráfico da função y=asen(bx), onde a≠0 e b>0.
Para o menor valor possível de b, os valores de a e b são, respectivamente:
a) - 3 e 2
b) 3 e 2
c) 3 e 1/2
d) - 3 e 1/2
11. (Fuvest) O menor valor de 1/ (3-cos x), com x real, é:
a)1/6
b)1/4
c)1/2
d)1
e)3
GABARITO:
1. D
2. 1/3 ≤ m ≤ 2/3
3. C
4. E
5. C
6. a) 2π/3
b) 2
c) π
d) π/4
7. B

4. 8.
9. B
10. B
11. B