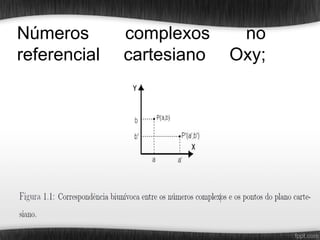
O documento aborda a interseção entre números complexos e geometria fractal, explorando conceitos como a representação algébrica e trigonométrica de números complexos, além de aplicações práticas da geometria fractal em diversas áreas como computação gráfica e previsão meteorológica. Destaca-se a formação de fractais, como o triângulo de Sierpinski e os conjuntos de Julia, em contextos dinâmicos, e menciona a teoria do caos e o 'efeito borboleta'. O documento também oferece referências relevantes para estudos adicionais sobre o tema.

1. Universidade Federal do Acre
–UFAC
Colégio de Aplicação – CAp
Turma: 301.
Disciplina: Matemática.
Docente: Dr. Gilberto Melo.
Discentes:
Todos da turma.

2. Números complexos e
Geometria Fractal
• Aplicação da geometria fractal;
• Números complexos;
• Representação algébrica do
número complexo “z”;
• Números complexos no referencial
cartesiano Oxy;

3. Números complexos e
Geometria Fractal
• Representação trigonométrica do
número complexo “z”;
• O triângulo de Sierpinski;
• Como são formados os “fractais”;
• Formas da natureza “auto-
semelhantes” do ponto de vista da
geometria fractal;

4. Números complexos e
Geometria Fractal
• Fractais em sistemas dinâmicos:
Formação dos conjuntos de Julia;
• A “Lei do crescimento (humano)”;
• Geometria fractal e a previsão de
tempo.

5. Aplicação da geometria fractal;
• A aplicação do Meio-tom digital refere-se
a um método de meio-tom digital que
utiliza curvas que preenchem o quadrado,
nomeadamente, a curva de Hilbert, para
reproduzir imagens monocromáticas.

6. Aplicação da geometria fractal;
• O método consiste na subdivisão da
imagem original em pequenas regiões
baseadas no traço da curva que preenche
o quadrado, em seguida são calculadas
as intensidades médias de cada região e
por fim determinam-se os padrões de
pontos da imagem.

7. Aplicação da geometria fractal;
• Esse método é aplicável a diversos
sectores da técnica tais como Indústria
gráfica, Impressão de Imagens
monocromáticas e/ou a cores,
Reprodução de meio-tom, computação
Gráfica, e Ilustração digital.

8. Números complexos;

9. Números complexos;

10. Representação algébrica do
número complexo “z”;

11. Representação algébrica do
número complexo “z”;

12. Números complexos no
referencial cartesiano Oxy;

13. Números complexos no
referencial cartesiano Oxy;

14. Representação trigonométrica
do número complexo “z”;

15. Representação trigonométrica
do número complexo “z”;

16. Representação trigonométrica
do número complexo “z”;

17. O triângulo de Sierpinski;

18. O triângulo de Sierpinski;

19. O triângulo de Sierpinski;

20. Como são formados os
“fractais”;

21. Como são formados os
“fractais”;

22. Como são formados os
“fractais”;

23. Formas da natureza do ponto de
vista da geometria fractal;

24. Formas da natureza do ponto de
vista da geometria fractal;

25. Formas da natureza do ponto de
vista da geometria fractal;

26. Formas da natureza do ponto de
vista da geometria fractal;

27. Fractais em sistemas dinâmicos:
Formação dos conjuntos de Julia;

28. Fractais em sistemas dinâmicos:
Formação dos conjuntos de Julia;

29. A “Lei do crescimento (humano)”;

30. A “Lei do crescimento (humano)”;

31. Geometria fractal e a previsão de
tempo.
• Teoria do caos: Caos determinístico;
• Um meteorologista do MIT chamado
Edward N. Lorenz ;
• Fractais de Lorenz;
• O “efeito borboleta”.

32. Referências
• FACULDADE DE CIÊNCIAS, Universidade do Porto. Geometria Fractal e
aplicações.
Disponível em:
<http://www.fc.up.pt/pessoas/jfalves/Teses/Raquel.pdf>
Acesso em: 21 nov. 2012.
• EVOLUINDO COM CONSCIÊNCIA. Aplicação dos fractais ao mercado de
capitais utilizando-se as Elliott Waves.
Disponível em:
<http://sofavoritosdanet.blogspot.com.br/2010/03/aplicacao-dos-fractais-ao-mercado-
de.html>
Acesso em: 21 nov. 2012.
• GNOSIS ONLINE.ORG. Fractais- Números complexos.
Disponível em:
<http://www.gnosisonline.org/wp-content/uploads/2010/08/Fractais-e-Crop-Circles.pdf>
Acesso em: 21 nov. 2012.

33. Fim de
Complexidade..
.