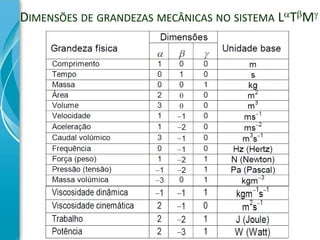
O documento discute análise dimensional, definindo grandezas fundamentais como comprimento, tempo e massa. Explica como definir dimensões de grandezas secundárias usando grandezas fundamentais e como equações devem ser dimensionalmente homogêneas. Também apresenta diferentes sistemas de unidades.

1. ANÁLISE DIMENSIONAL
1.ª Aula Prática
Dídia Isabel Cameira Covas
IST, 16 de fevereiro de 2012

2. GRANDEZAS FUNDAMENTAIS, DIMENSÕES E
UNIDADES
 Qualquer grandeza mecânica pode ser definida a
partir de três grandezas independentes:
– o comprimento, L (length)
– o tempo, T (time)
– a massa, M (mass)
 A temperatura, , também é uma grandeza
fundamental mas não intervém nas equações da
mecânica

3. GRANDEZAS FUNDAMENTAIS, DIMENSÕES E
UNIDADES
 Equação de definição de uma grandeza X
X=A*B
– Por exemplo
• Trabalho W= F * x
 Equação das dimensões da grandeza X
[X] = [A * B] = L T M
Sendo
, ,  = dimensões da grandeza
L ,T, M = grandezas fundamentais
X = grandeza secundária
– Por exemplo
• [V] = [ x / t] = L / T = L T-1

4. GRANDEZAS FUNDAMENTAIS, DIMENSÕES E
UNIDADES
 Uma grandeza é adimensional quando  = =  = 0
 Uma grandeza é dimensional quando pelo menos
uma das dimensões é não nula. Esta pode ser:
– Grandeza geométrica: se  0 e =  = 0
– Grandeza cinemática: se  0 e  = 0
– Grandeza dinâmica: se  0
 Uma equação é dimensionalmente homogénea
quando ambos os membros têm as mesmas
dimensões

5. GRANDEZAS FUNDAMENTAIS, DIMENSÕES E
UNIDADES
 Sejam três grandezas a1, a2 e a3 tais que
[a1] = L1 T1 M1
[a2] = L2 T2 M2
[a3] = L3 T3 M3
 Se o determinante de for nulo,
as grandezas são dependentes;
se for não nulo, então são independentes

6. GRANDEZAS FUNDAMENTAIS, DIMENSÕES E
UNIDADES
 Unidades exprimem uma grandeza num sistema
métrico
– Exemplo: trabalho (W)  Joule, N.m
 Sistemas de unidades
– LTM (length, time, mass)
• Sistema Internacional de unidades (SI): m, s, kg
• Sistema CGS: cm, s, g
– LTF(length, time, force)
• Sistema Métrico Gravitatório: m, s, kgf
• Sistema Industrial Inglês: pé, s, libra
1 libra = 0,4536 kgf; 1 pé = 0,3048 m

7. EXEMPLO 1.4

8. DIMENSÕES DE GRANDEZAS MECÂNICAS NO SISTEMA LTM

9. TEOREMA DE VASCHY-BUCKINGHAM
OU TEOREMA DOS 
Toda a relação dimensionalmente homogénea entre n
grandezas físicas:
 (a1, a2, …., an)=0
pode ser substituida por outra relação entre (n-p)
parâmetros adimensionais:
’ (1, 2, …., n-p)=0
sendo p = n.º de grandezas dimensionalmente
independentes

10. PROCEDIMENTO
 Identificar as n variáveis (grandezas físicas) que
caracterizam o fenómeno:  (a1, a2, …., an)=0
 Escolher p grandezas fundamentais independentes
(admita que se conhecem à partida): a1, a2, a3 ,….
 Estabelecer n-p parâmetros adimensionais com base
no rácio entre as grandezas restantes e as
fundamentais (a1, a2, a3):
(simplificação mi=1)
 Determinar os expoentes xi, yi, zi por forma a que i
seja adimensional
 Escrever a relação ’ (1, 2, …., n-p)=0

11. EXEMPLO 1.5