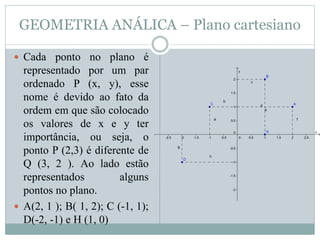
O documento apresenta os conceitos básicos de geometria analítica, incluindo o plano cartesiano, representação de pontos, teorema de Pitágoras e a fórmula para calcular a distância entre dois pontos no plano. Também fornece um breve histórico sobre René Descartes e sua contribuição para a geometria analítica.

1. GEOMETRIA ANÁLICA
 O objetivo desta aula é
apresentar de forma
clara e objetiva, como se
encontra a distância
entre dois pontos no
plano cartesiano. Para
isso seguiremos o
seguinte cronograma.
 Apresentar o plano
cartesiano e uma breve
história sobre René
Descartes;
 Representar pontos no
plano;
 Teorema de Pitágoras;
 Dedução da equação da
distância entre dois
pontos.

2. GEOMETRIA ANÁLICA – Plano cartesiano
Criado por René Descartes
(1596-1950), o plano
cartesiano é uma ferramenta
utilíssima para representação
figuras geométricas e
gráficos de funções. Ele é
formando por duas retas
perpendiculares,que dividem
o plano em quatro partes,
que chamamos de quadrantes
como na figura ao lado.
O ponto de interseção das
duas retas é chamado de
origem. O eixo dos xx é
chamado de abscissa e o eixo
dos yy de ordenada.
1º quadrante = x > 0 e y > 0
2º quadrante = x < 0 e y > 0
3º quadrante = x < 0 e y < 0
4º quadrante = x > 0 e y < 0

3. GEOMETRIA ANÁLICA – Plano cartesiano
 Cada ponto no plano é
representado por um par
ordenado P (x, y), esse
nome é devido ao fato da
ordem em que são colocado
os valores de x e y ter
importância, ou seja, o
ponto P (2,3) é diferente de
Q (3, 2 ). Ao lado estão
representados alguns
pontos no plano.
 A(2, 1 ); B( 1, 2); C (-1, 1);
D(-2, -1) e H (1, 0)

4. GEOMETRIA ANÁLICA – HISTÓRIA
 René Descartes nasceu em (
La Haye em Touraine, 31 de
março de 1596) foi um
filosofo, físico e matemático
francês. Durante a Idade
Moderna também era
conhecido por seu nome
latino Renatus Cartesius.
 Notabilizou-se sobretudo por
seu trabalho revolucionário na
filosofiae na ciência, mas
também obteve
reconhecimento matemático
por sugerir a fusão da álgebra
com a geometria,
fato que gerou a geometria
analítica e o sistema de
coordenadas que hoje leva o
seu nome.
René Descartes morreu de
pneumonia no dia 11 de
Fevereiro de 1650, em
Estocolmo, onde estava
trabalhando como professor a
convite da Rainha.

5. GEOMETRIA ANÁLICA – distância entre pontos
 Para encontrar a distância
entre dois pontos, faremos
uso do teorema de
Pitágoras, relembrando que
o teorema garante que em
um triângulo retângulo, a
soma dos quadrados dos
catetos é igual ao quadrado
da hipotenusa. Conforme
figura ao lado.
𝑎2
= 𝑏2
+ 𝑐2

6. GEOMETRIA ANÁLICA – distância entre pontos
 Dados dois pontos
quaisquer do plano A (x, y)
e B (w, z), como mostra a
figura;
 Observando o gráfico
notamos que:
O triângulo ABF é
retângulo; o segmentos de
reta b e c são as distância:
b = z-y e c = w-z e “a” é a
distância que queremos
descobrir, ou seja a
hipotenusa do triângulo.
Aplicando o teorema de
Pitágoras temos:
𝑎2
= 𝑏2
+ 𝑐2
𝑎2
= 𝑧 − 𝑦 2
+ 𝑤 − 𝑧 2
𝑎 = 𝑧 − 𝑦 2 𝑤 − 𝑧 2

7. GEOMETRIA ANÁLICA – distância entre pontos
 Geralmente, ao invés de utilizar a letra “a” para representar a
distância entre dois pois A e B, representamos por:
 Podemos reescrever a equação o slide anterior como:
𝑑(𝐴,𝐵)

8. GEOMETRIA ANÁLICA - Exemplo
 Exemplo
1- Encontrar a distância entre
os pontos A (3, 4) e B (-4,4)
Resolução:
 1- Encontrar a distância
entre os pontos A (2, -3) e
B (7, 9)
 Resolução:
𝑑 𝐴,𝐵 = 3 − (−4) 2+ 4 − 4 2
𝑑 𝐴,𝐵 = 7 2+ 0 2
𝑑 𝐴,𝐵 = 49
𝑑 𝐴,𝐵 = 7
𝑑 𝐴,𝐵 = 2 − 7) 2+ −3 − 9 2
𝑑 𝐴,𝐵 = −5 2+ −12 2
𝑑 𝐴,𝐵 = 25 + 144
𝑑 𝐴,𝐵 = 169
𝑑 𝐴,𝐵 = 13

9. GEOMETRIA ANÁLICA - Exercício
 Exercício
1– Dados três pontos A(2, 3),
B(2, 0) e C(3,0), determinar
o perímetro do triângulo
formado por esses pontos.
Resposta: Representando
graficamente temos:
A estratégia para resolver o problema
consiste em encontrar a distância
entre cada ponto e depois somá-las:
10
𝑑𝑖𝑠𝑡â𝑛𝑐𝑖𝑎 𝑑𝑒 𝐴 𝑎 𝐵: 𝑑 𝐴,𝐵
= 2 − 2 2 + 3 − 0 2 = 3
20
𝑑𝑖𝑠𝑡â𝑛𝑐𝑖𝑎 𝑑𝑒 𝐴 𝑎 𝐶: 𝑑 𝐴,𝐶
= 2 − 3 2 + 3 − 0 2 = 1
30
𝑑𝑖𝑠𝑡â𝑛𝑐𝑖𝑎 𝑑𝑒 𝐵 𝑎 𝐶: 𝑑 𝐵,𝐶
= 2 − 3 2 + 0 − 0 2 = 1
O perímetro é dado por:
𝑃 = 𝑑 𝐴,𝐵 + 𝑑 𝐴,𝐶 + 𝑑 𝐵,𝐶
𝑃 = 3 + 1 + 1 = 5