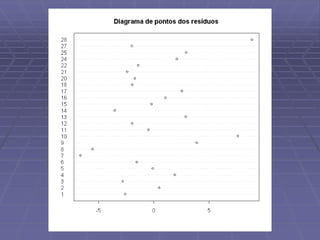
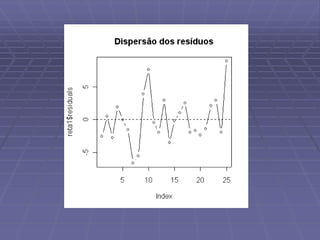
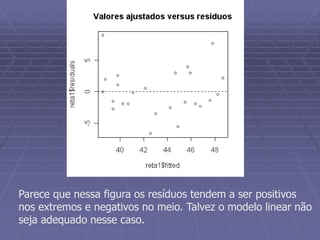
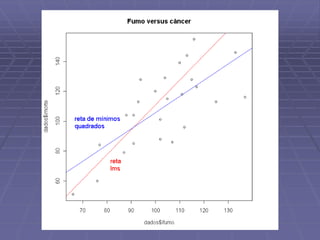
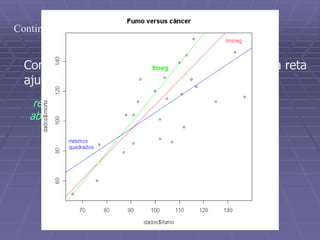
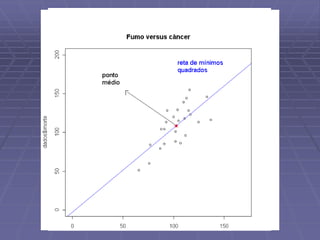
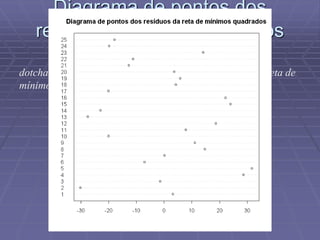
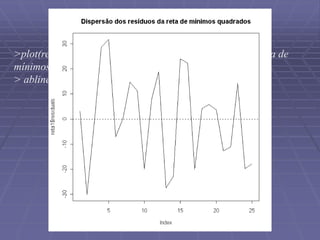
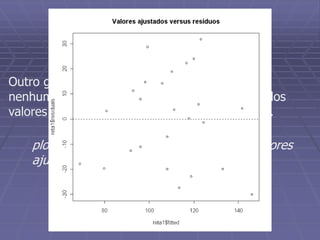
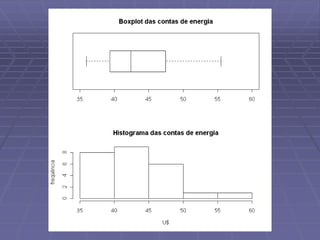
Este documento discute análise exploratória de dados e ajuste de modelos lineares. Ele apresenta o objetivo de obter uma reta que se ajuste aos dados usando critérios de mínimos quadrados e métodos robustos. Também discute análises exploratórias de resíduos para validar o modelo ajustado.

1. Análise Exploratória de
Dados
R – LIG/09 – maio de 2006

2. Objetivos
 obter uma reta que se ajuste aos dados
segundo o critério de mínimos quadrados;
 apresentar outros critérios para a
determinação de uma reta que se ajuste
aos dados;
 realizar análises exploratórias dos
resíduos do modelo ajustado.
Análise de duas variáveis quantitativas:

3. Critério de mínimos quadrados
 Como são obtidos os coeficientes da reta
de mínimos quadrados?
Nossos dados podem ser pensados como uma coleção
bivariada:
),(),...,,(),,( 2211 nn yxyxyx
Foi considerado adequado o modelo x 
para explicar y .

4. Critério de mínimos quadrados
Resíduo (ri): diferença entre o valor observado da
variável resposta e o valor ajustado pelo modelo:
)(ˆ iiiii bxayyyr 
valor
observado
valor ajustado
pelo modelo

5. Critério de Mínimos Quadrados
 Escolha =a e =b de tal maneira que a
soma de quadrados dos resíduos seja um
mínimo.
Minimizar
2
11
2
)(),( i
n
i
i
n
i
i xyrf   


6. Coeficientes da reta de mínimos
quadrados
 Solução:
2
1
1
)(
))((






 n
i
i
n
i
ii
xx
xxyy
b
xbya 
Coeficiente de inclinação da reta
Coeficiente linear da reta (intercepto)

7. Coeficientes da reta de mínimos
quadrados

























n
i
n
i
i
i
n
i
n
i
i
n
i
i
ii
n
i
i
n
i
ii
n
x
x
n
yx
yx
xx
xxyy
b
1
2
12
1
11
2
1
1
)(
))((
Coeficiente angular da reta de mínimos quadrados

8. Exemplo 1: Idade versus altura1
 Fonte: http://lib.stat.cmu.edu/DASL/
 Referência: Moore, David S., and George P.
McCabe (1989). Introduction to the Practice of
Statistics, p. 118.
 A altura de uma criança aumenta ao longo do
tempo. Como o padrão de crescimento varia de
criança para criança, uma forma de
compreender o padrão geral de crescimento é
usar a média das alturas de várias crianças,
como é feito com os dados a seguir.

9. Idade versus altura
 Descrição: Alturas médias de um grupo de crianças de
Kalama, um povoado egípcio que é o local de um estudo
de nutrição em países em desenvolvimento. Os dados
foram obtidos medindo-se as alturas de 161 crianças no
povoado cada mês.
 Número de casos: 12
 Nomes das variáveis:
 idade: idade em meses
 altura: altura média em cm

10. Idade versus altura: Dados
 idade altura
 18 76.1
 19 77
 20 78.1
 21 78.2
 22 78.8
 23 79.7
 24 79.9
 25 81.1
 26 81.2
 27 81.8
 28 82.8
 29 83.5

11. Idade versus altura
 Investigue possíveis relações entre idade
e altura nesta base de dados.
 Diagrama de dispersão
 Coeficiente de correlação
 Os dados estão no arquivo idadealtura.txt,
com a primeira linha indicando os nomes
das variáveis.

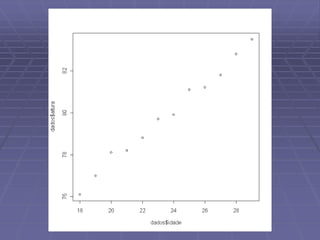
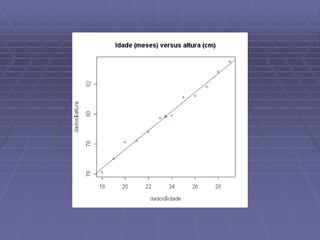
13. cor(dados$idade,dados$altura)
[1] 0.994366
É visível a forte relação entre a idade em meses e a altura!

14. Comentário
A altura de uma criança não é estável, mas cresce ao longo do
tempo. Como o padrão de crescimento varia de criança para criança,
uma forma de compreender o modelo geral de crescimento é usar a
média de altura de várias crianças, como apresentado neste conjunto
de dados.
O diagrama de dispersão da altura versus idade é quase
uma linha reta, mostrando um modelo de crescimento linear.

15. Extrapolação
 Deve-se tomar cuidado com previsões fora
do campo de variação da variável explicativa.
 Quanto mais distante estiver o valor da
variável explicativa do conjunto de valores
efetivamente observado, mais imprecisa será
a previsão.
 De fato, nada garante que fora deste
intervalo, a relação linear obtida continue
valendo.

16. Comentários
 O caso deste exemplo é típico.
 A altura média pode crescer linearmente
com a idade em meses nos primeiros anos
de vida, mas a curva de altura de uma
pessoa certamente não é linear ao longo de
sua vida!
 Quando falamos em modelos, uma das
coisas que se deve ter em mente é a
abrangência deles.

17. Reta de mínimos quadrados
 reta1=lm(dados$altura~dados$idade)
 Coefficients:
 (Intercept) dados$idade
 64.928 0.635
Modelo ajustado:
altura=64.928+0.635xidade
variável
resposta
variável
explicativa
Coef. linear
Coef. angular

19. Outros métodos para obter a reta
O critério de minimização da soma dos resíduos ao
quadrado não é o único!
Há outros critérios para obter uma reta que se ajuste aos
dados.
Um deles é minimizar a soma dos resíduos tomados em
valor absoluto.
Este critério é conhecido como critério L1.
 

n
i
ii
n
i
i xyr
11
|| 
Escolha  e  de modo a minimizar:

20. Métodos robustos de ajuste da reta
Métodos conhecidos como robustos, envolvem minimizar
alguma função dos resíduos ao quadrado ordenados.
1) (lmsreg) least median squares:
escolha  e  de modo a minimizar:
},...,1),{(
2
nirmediana i 
Neste caso, não há uma solução analítica como no caso do critério de
mínimos quadrados. O algoritmo para a obtenção dos coeficientes é bem
mais complexo.
O R possui uma função que nos retorna os coeficientes
da reta resultantes, com base nesse critério: lmsreg no
pacote MASS.

21. Métodos robustos de ajuste da reta
Para usar funções do pacote MASS, há a
necessidade de carregar o pacote.
O único pacote que não precisa ser carregado no R
é o base, que contém as funções básicas que
trabalhamos até agora (pie,
barplot,mean,sd,summary,boxplot,
quantile,plot,lm,round,etc.)

22. Carregando o pacote MASS
Clique em
1) Packages (barra de menus na parte superior da tela)
2) load packages
3) MASS

23. Exemplo 2
Voltemos aos dados do arquivo fumo.txt, trabalhados na
aula passada.
Compare as retas de mínimos quadrados e via critério lms
(least median squares) (lmsreg).
dados=read.table
(“http://www.im.ufrj.br/~flavia/aed06/fumo.txt”,header=T)
reta1=lm(dados$imorte~dados$ifumo)
reta2=lmsreg(dados$imorte~dados$ifumo)
plot(dados$ifumo,dados$imorte,main=“Fumo versus câncer”)
abline(reta1$coefficients,col=“blue”)
abline(reta2$coefficientes,col=“red”)

25. Métodos robustos de ajuste da reta
2) Um outro método é o lts (least trimmed squares)
que consiste em
escolha  e  de modo a minimizar: 
h
i ir1
2
)(
onde r(i) representa os resíduos ordenados, i=1,...,n, e h
é um natural menor que n, ou seja, minimiza-se a soma
dos h menores resíduos ao quadrado.
No R a função que realiza este ajuste também está
disponível no pacote MASS: ltsreg.

26. Continuação do exemplo
Compare com os outros dois ajustes obtidos, a reta
ajustada via ltsreg.
reta3=ltsreg(dados$imorte~dados$ifumo)
abline(reta3$coefficients,col=“green”)

28. Comentários
Quando o conjunto de dados não apresentar
observações muito diferentes das demais (outliers)
e o comportamento da variável dependente
(resposta) for aproximadamente “normal”, não
haverá muita diferença entre as retas obtidas por
métodos robustos e a reta de mínimos quadrados.

29. Comentários
Depois de ajustado um modelo é fundamental realizar a
etapa de verificação do modelo em que boa parte consiste
numa análise exploratória detalhada dos resíduos do
modelo.
Apenas após a etapa de validação e a escolha do modelo é
que podemos partir para a etapa de previsões.

30. Análise dos resíduos
Por exemplo, o diagrama de pontos dos resíduos
NÃO deve apresentar nenhuma estrutura aparente.
Caso, o diagrama de pontos apresente alguma
estrutura é sinal de que o modelo proposto para os
dados ainda não está suficientemente adequado e
deve ser reformulado.
Vejamos como está o diagrama dos resíduos da
reta de mínimos quadrados para este último ajuste.

31. Diagrama de pontos dos
resíduos da reta de mínimos
quadrados
dotchart(reta1$residuals,main=“Diagrama de pontos da reta de
mínimos quadrados”)

32. Outra possibilidade
>plot(reta1$residuals,main="Dispersão dos resíduos da reta de
mínimos quadrados",type=”l")
> abline(h=0,lty=2)

33. Resíduos versus valores
ajustados
Outro gráfico que também não deve apresentar
nenhuma estrutura é o diagrama de dispersão dos
valores ajustados versus os resíduos do modelo.
plot(reta1$fitted,reta1$residuals,main=“Valores
ajustados versus resíduos”)

34. Outros critérios
Construa o diagrama de pontos dos resíduos e o
diagrama de dispersão dos resíduos versus valores
ajustados para os outros dois ajustes deste exemplo
(reta2 e reta3).

35. Exemplo 3: Contas de energia
Os dados a seguir referem-se à temperatura média mensal
e a quantidade de energia elétrica (em $) na conta mensal.
Os dados foram armazenados no arquivo energia.txt
os nomes das variáveis são data, temp e conta.
Fonte: Rossman & Chance (1998). Workshop Statistics:
Discovery with data and Minitab.
Springer. (Capítulo 9, pg. 159).

36. Contas de energia (cont.)
Antes de examinar a relação entre temperatura
média e conta de energia, examine a distribuição
dos dados referentes a contas de energia. Descreva
a forma da distribuição dos valores das contas.
Construa o diagrama de dispersão de temperatura
versus conta e avalie uma possível associação
positiva ou negativa entre estas variáveis.

39. Contas de energia (cont.)
Observe que em regiões com temperaturas muito
baixas, diferente de regiões quentes, o consumo de
energia é maior quanto menor for a temperatura!
Calcule a correlação entre temperatura e conta de
energia.
Obtenha as retas de mínimos quadrados, lms e lts
para estes dados.

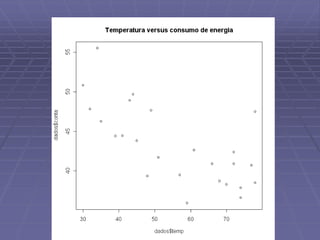
40. > cor(dados$temp,dados$conta)
[1] -0.6883143
reta1=lm(dados$conta~dados$temp)

42. Coefficients:
(Intercept) dados$temp
55.0286 -0.2112
Modelo ajustado:
Conta=55.0286-0.2112x(temperatura)

43. Contas de energia (cont.)
Usando a reta de mínimos quadrados, determine o resíduo
e o valor ajustado para o mês de março de 1992.
Faça um boxplot dos resíduos da reta de mínimos
quadrados e verifique se há algum ponto exterior. Em caso
afirmativo, identifique qual a data a que este resíduo se
refere.

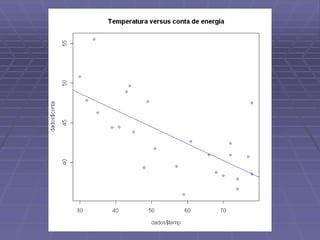
44. > reta1$residuals[12]
12
-1.937377
> reta1$fitted[12]
12
46.36738
12 mar/92: temp=41, conta=44.43

46. É possível verirficar que a observação cujo
resíduo é um ponto exterior no boxplot é a de
julho de 1993.

47. Contas de energia (cont.)
Faça um dotchart dos resíduos e comente sobre a
forma do mesmo.
“Um modelo é adequado entre outras coisas, se o
diagrama de pontos dos resíduos não apresentar
nenhum tipo de estrutura”.
De acordo com a afirmação anterior, você diria que
o modelo é adequado?

50. Parece que nessa figura os resíduos tendem a ser positivos
nos extremos e negativos no meio. Talvez o modelo linear não
seja adequado nesse caso.

51. Retas robustas
 Investigue o comportamento dos resíduos
para os critérios lms e lts.