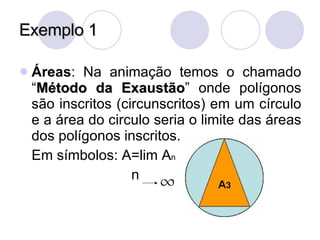
1) O cálculo é um ramo da matemática que trata de limites e conceitos dinâmicos como variação e movimento. 2) O cálculo generaliza conceitos como área e tangente à curva usando o conceito de limites, como aproximar a área de uma curva pelo limite das áreas de polígonos inscritos. 3) O cálculo permite calcular velocidades instantâneas, declividades, comprimentos de curvas e áreas sob curvas como limites.

1. CÁLCULO A Cálculo Diferencial e Integral Uma visão informal

2. O QUE É O CÁLCULO DIFERENCIAL E INTEGRAL? A matemática que você estudou até agora é quase estática . O cálculo, porém é dinâmico . O cálculo diz respeito a Variação e Movimento O cálculo relaciona quantidades e generaliza conceitos já estudados, introduzindo a importante idéia de Limites

3. Exemplo 1 Áreas : Na animação temos o chamado “ Método da Exaustão ” onde polígonos são inscritos (circunscritos) em um círculo e a área do circulo seria o limite das áreas dos polígonos inscritos. Em símbolos: A=lim A n n

4. Exemplo 2 Neste exemplo, a animação mostra que para calcular a área de uma curva, aproxima-se esta área por áreas de retângulos e obtem-se a área pedida, calculando-se o limite das somas das áreas desses retângulos.

5. Exemplo 3 Tangente à uma curva: Uma idéia de limites pode ser usada também quando se tem uma curva e procura-se a inclinação da reta tangente t no ponto P =(a,f(a)) Para isto basta tomar um outro ponto Q=(x,f(x)) e trocar a secante m= f(x)-f(a) x-a

6. Pense no ponto Q movendo-se ao longo da curva em direção ao ponto P que a inclinação da reta tangente é m = lim f(x)-f(a) x a x-a

7. Conclusão O cálculo é um ramo da matemática que trata de limites. O que é a velocidade instantânea? É o limite das velocidades médias. O que é declividade de uma curva? É o limite das declividades das secantes. O que é o comprimento de uma curva? É o limite do comprimento dos polígonos inscritos O que é a soma de uma série infinita? É o limite das somas dos termos finitos(Paradoxo de Zenon) Qual a área sob uma região com uma curva? É o limite das áreas das regiões limitadas pelas retas