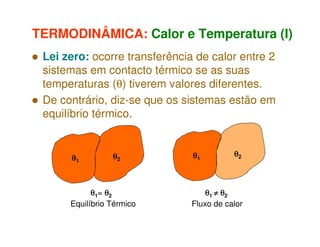
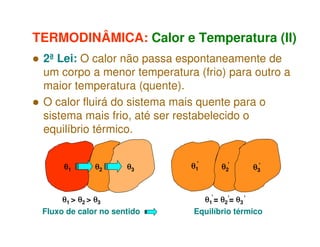
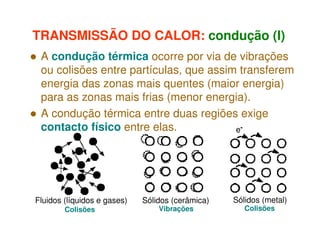
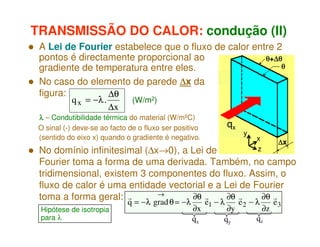
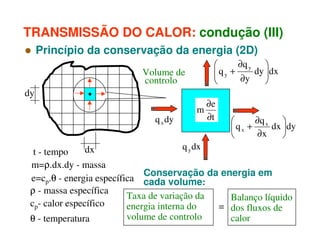
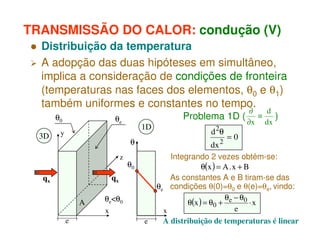
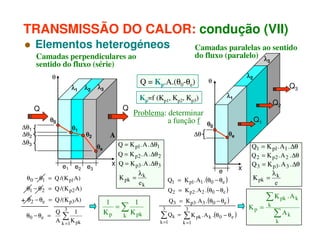
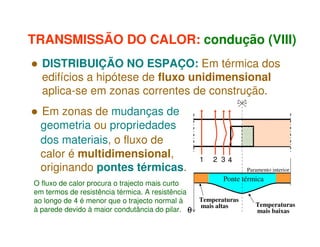
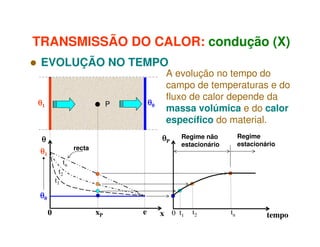
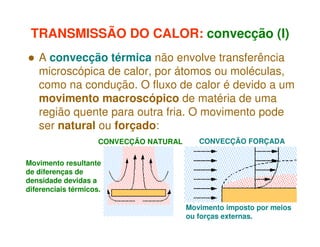
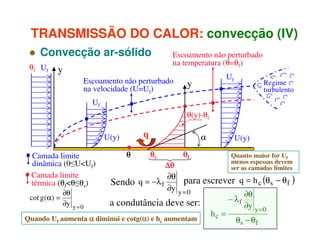
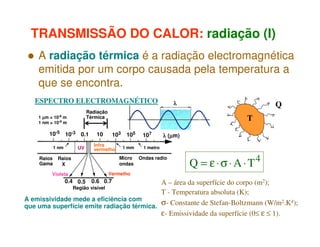
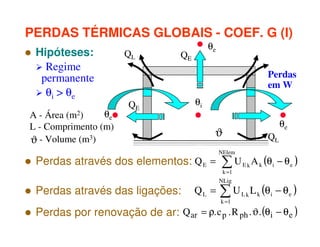
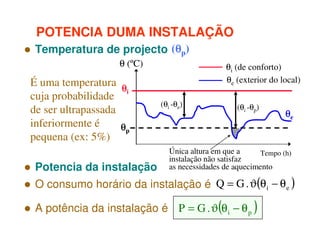
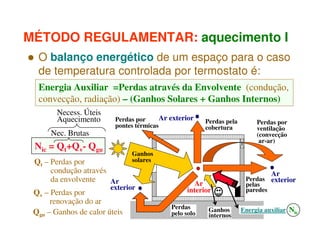
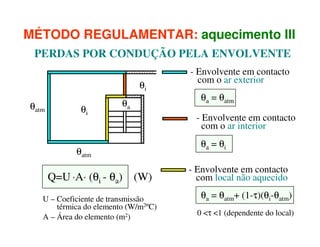
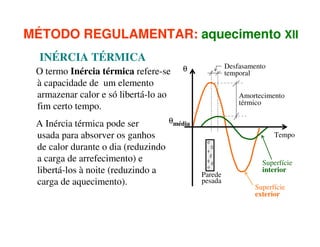
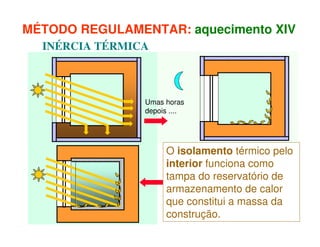
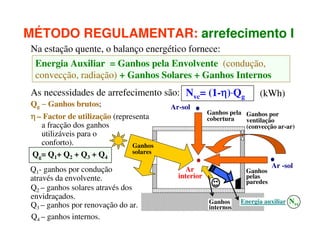
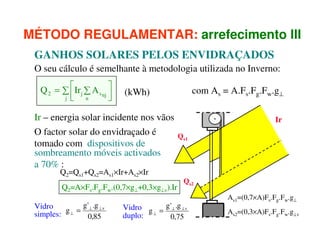
1) O documento discute os princípios da transmissão de calor em edifícios, incluindo condução, convecção e radiação. 2) A condução ocorre por vibrações ou colisões a nível molecular, enquanto a convecção envolve o movimento macroscópico de matéria motivado por diferenças de temperatura. 3) As necessidades energéticas de aquecimento e arrefecimento de edifícios podem ser estimadas usando métodos regulamentares que levam em conta os ganhos e perdas de

1. TÉRMICA DE EDIFÍCIOS
Transmissão do calor e necessidades
energéticas
António Moret Rodrigues
IST

2. ÍNDICE
Termodinâmica: calor e temperatura (2 slides)
Transmissão do Calor:
Condução (10 slides)
Convecção (5 slides)
Radiação (5 slides)
Coeficiente de transmissão Térmica (1 slide)
Perdas térmicas globais – Coef. G (3 slides)
Potência duma instalação (1 slide)
Necessidades energéticas de edifícios:
Método regulamentar: aquecimento (14 slides)
Método regulamentar: arrefecimento (4 slides)

3. TERMODINÂMICA: Calor e Temperatura (I)
Lei zero: ocorre transferência de calor entre 2
sistemas em contacto térmico se as suas
temperaturas (θ) tiverem valores diferentes.
De contrário, diz-se que os sistemas estão em
equilíbrio térmico.
θ1
θ2
θ1= θ2
Equilíbrio Térmico
θ1
θ2
θ1 ≠ θ2
Fluxo de calor

4. TERMODINÂMICA: Calor e Temperatura (II)
2ª Lei: O calor não passa espontaneamente de
um corpo a menor temperatura (frio) para outro a
maior temperatura (quente).
O calor fluirá do sistema mais quente para o
sistema mais frio, até ser restabelecido o
equilíbrio térmico.
θ1
θ2
θ3
θ1 > θ2 > θ3
Fluxo de calor no sentido
,
,
θ1
,
θ2
,
,
θ3
,
θ1 = θ2 = θ3
Equilíbrio térmico

5. TRANSMISSÃO DO CALOR: condução (I)
A condução térmica ocorre por via de vibrações
ou colisões entre partículas, que assim transferem
energia das zonas mais quentes (maior energia)
para as zonas mais frias (menor energia).
A condução térmica entre duas regiões exige
contacto físico entre elas.
e-
Fluidos (líquidos e gases)
Colisões
Sólidos (cerâmica)
Vibrações
Sólidos (metal)
Colisões

6. TRANSMISSÃO DO CALOR: condução (II)
A Lei de Fourier estabelece que o fluxo de calor entre 2
pontos é directamente proporcional ao
θ+∆θ
∆
θ
gradiente de temperatura entre eles.
No caso do elemento de parede ∆x da
figura:
∆θ
q x = −λ .
(W/m2)
∆x
λ – Condutibilidade térmica do material (W/mºC)
O sinal (-) deve-se ao facto de o fluxo ser positivo
(sentido do eixo x) quando o gradiente é negativo.
qx
y
x
z
∆x
No domínio infinitesimal (∆x→0), a Lei de
Fourier toma a forma de uma derivada. Também, no campo
tridimensional, existem 3 componentes do fluxo. Assim, o
fluxo de calor é uma entidade vectorial e a Lei de Fourier
→
∂θ r
∂θ r
∂θ r
toma a forma geral: r
Hipótese de isotropia
para λ
q = −λ grad θ = −λ
∂x
qx
e1 − λ
∂y
qy
e2 − λ
∂z
qz
e3

7. TRANSMISSÃO DO CALOR: condução (III)
Princípio da conservação da energia (2D)
∂q y 

qy +
dy dx


∂y


Volume de
controlo
dy
q x dy
m
∂e
∂t
∂q x


dx dy
qx +
∂x


q y dx
dx
t - tempo
m=ρ.dx.dy - massa
Conservação da energia em
e=cp.θ - energia específica cada volume:
ρ - massa específica
Taxa de variação da
Balanço líquido
cp- calor específico
energia interna do
= dos fluxos de
volume de controlo
calor
θ - temperatura

8. TRANSMISSÃO DO CALOR: condução (IV)
Equação geral da condução (2D)
A aplicação do princípio da conservação da
∂q y
∂q x
∂e
dx . dy
energia fornece: ρ . dx . dy = − dx . dy −
∂t
∂x
∂y
Taxa de variação Balanço líquido dos fluxos
da energia
Utilizando a lei de Fourier e expressando a
energia interna em função da temperatura:
 ∂ 2θ ∂ 2θ 
∂θ

= α
+
2
2
 ∂x
∂t
∂y 

ou, na forma compacta,
com α =
Casos particulares
∂θ
= α∇ 2 θ
∂t
λ
- difusibilidade térmica
ρ.c p
∂ 2θ ∂ 2θ
∂θ
+
=0
= 0 ⇒ Regime estacionário ou permanente ⇒
2
2
∂t
∂x
∂y
∂θ
∂ 2θ
∂θ
=α
= 0 ⇒ Condução térmica unidimensional (1D) ⇒
∂y
∂t
∂x 2

9. TRANSMISSÃO DO CALOR: condução (V)
Distribuição da temperatura
A adopção das duas hipóteses em simultâneo,
implica a consideração de condições de fronteira
(temperaturas nas faces dos elementos, θ0 e θ1)
também uniformes e constantes no tempo.
θ0
3D
Problema 1D (
θe
1D
y
2
θ
z
θ0
qx
qx
A
e
d 2θ
θe<θ0
x
e
=0
∂
d
≡
)
∂x dx
dx
Integrando 2 vezes obtém-se:
θ(x ) = A . x + B
As constantes A e B tiram-se das
θe condições θ(0)=θ0 e θ(e)=θe, vindo:
θ −θ
θ(x ) = θ0 + e 0 ⋅ x
e
x
A distribuição de temperaturas é linear

10. TRANSMISSÃO DO CALOR: condução (VI)
Fluxo de calor
O fluxo de calor unitário (unidade de área) que
atravessa o elemento tira-se directamente da Lei
de Fourier q=qx=-λ(∂θ/∂x), pois qy=qz=0.
Sendo ∂θ/∂x=dθ/dx=(θ1-θ0)/e, vem:
θ − θ0
q = −λ e
e
O fluxo de calor que atravessa a totalidade do
elemento é: Q = q . dA = q . dA = − λ A(θe − θ0 )
∫A
∫A
e
Ignorando o sinal (o sentido do fluxo é conhecido):
λ
(condutância térmica)
Q = K p . A . (θe − θ0 ) com K p =
e
O inverso da condutância (W/m2ºC) toma o nome
de resistência térmica: Rp=1/Kp (m2ºC/W).

11. TRANSMISSÃO DO CALOR: condução (VII)
Elementos heterogéneos
Camadas paralelas ao sentido
do fluxo (paralelo) λ
Camadas perpendiculares ao
sentido do fluxo (série)
θ
λ1
λ2
3
Q = Kp.A.(θ0-θe)
λ3
Q
∆θ1
∆θ2
∆θ3
θ0
θ1
θe
θ 0 − θ1 = Q /(K p1A)
θ1 − θ 2 = Q /(K p 2 A)
+ θ2 − θe = Q /(K p3A)
3
θ0 − θe =
A
θ2
e1 e2 e3
Q
1
∑K
A k =1 pk
Problema: determinar
a função f
Q1
θe
e
Q1 = K p1. A1 . (θ0 − θe )
Q 2 = K p2 . A 2 . (θ0 − θe )
Q3 = K p3. A3 . (θ0 − θe )
3
3
k =1
k =1
Q2
θ0
∆θ
Q = K p1. A . ∆θ1
Q = K p 2 . A . ∆θ 2
x Q = K p3 . A . ∆θ3
λ
K pk = k
ek
1
1
=∑
Kp
K pk
k
Q3
λ1
Kp=f (Kp1, Kp2, Kp3)
Q
λ2
θ
∑ Q k = ∑ K pk . A k .(θ 0 − θ e )
x
Q1 = K p1. A1 . ∆θ
Q 2 = K p 2 . A 2 . ∆θ
Q 3 = K p3 . A 3 . ∆θ
λ
K pk = k
e
∑ K pk . A k
Kp = k
∑ Ak
k

12. TRANSMISSÃO DO CALOR: condução (VIII)
DISTRIBUIÇÃO NO ESPAÇO: Em térmica dos
edifícios a hipótese de fluxo unidimensional
aplica-se em zonas correntes de construção.
Em zonas de mudanças de
geometria ou propriedades
dos materiais, o fluxo de
calor é multidimensional,
originando pontes térmicas.
O fluxo de calor procura o trajecto mais curto
em termos de resistência térmica. A resistência
ao longo de 4 é menor que o trajecto normal à
à parede devido à maior condutância do pilar. θ
1
2 34
Paramento interior
Ponte térmica
Temperaturas
mais altas
Temperaturas
mais baixas

13. TRANSMISSÃO DO CALOR: condução (IX)
As pontes térmicas podem constituir um factor
importante de redução da qualidade térmica duma
construção, não só pelo acréscimo de perdas
(ganhos) de calor mas
também porque cresce o
risco de condensações.
Nas pontes térmicas as
temperaturas são mais
baixas no paramento
interior e mais altas no
exterior relativamente à
zona corrente.

14. TRANSMISSÃO DO CALOR: condução (X)
EVOLUÇÃO NO TEMPO
θ10
T
θ0
P
A evolução no tempo do
campo de temperaturas e do
fluxo de calor depende da
massa volúmica e do calor
específico do material.
θP
θ
θ1
recta
Regime
estacionário
Regime não
estacionário
tn
t2
t1
θ0
0
xP
e
x 0 t1
t2
tn
tempo

15. TRANSMISSÃO DO CALOR: convecção (I)
A convecção térmica não envolve transferência
microscópica de calor, por átomos ou moléculas,
como na condução. O fluxo de calor é devido a um
movimento macroscópico de matéria de uma
região quente para outra fria. O movimento pode
ser natural ou forçado:
CONVECÇÃO NATURAL
CONVECÇÃO FORÇADA
Movimento resultante
de diferenças de
densidade devidas a
diferenciais térmicos.
Movimento imposto por meios
ou forças externas.

16. TRANSMISSÃO DO CALOR: convecção (II)
Em térmica dos edifícios distinguem-se duas
situações típicas de transferência de calor por
convecção: ar-sólido e ar-ar.
Convecção ar-sólido: trocas de calor entre o
ambiente (interno ou externo) e as superfícies da
envolvente (paredes, tectos, pavimentos).
Convecção ar-ar: trocas de calor entre massas de
ar exterior e interior, através das aberturas da
envolvente (ventilação através de janelas,
condutas; infiltrações através de frinchas, juntas).

17. TRANSMISSÃO DO CALOR: convecção (III)
Forma de expressão da convecção
Atendendo à expressão encontrada para
transmissão do calor por condução, é de toda a
conveniência a aplicação à convecção duma
expressão linear do mesmo tipo: q = c.∆θ
∆θ,
∆θ
variando c e ∆θ com o tipo de convecção.
Convecção ar-sólido
θs
As trocas de calor entre a superfície (s) Q
e o ar (f) confinante são expressas
θf
pela lei de Newton do arrefecimento:
Q = hc.A.(θs- θf)
(W)
A
hc – Condutância térmica superficial por convecção (W/m2ºC).

18. TRANSMISSÃO DO CALOR: convecção (IV)
Convecção ar-sólido
θf Uf
y
Escoamento não perturbado
na temperatura (θ=θf)
Escoamento não perturbado
na velocidade (U=Uf)
Uf
y
Regime
turbulento
Uf
θ(y)-θf
q
U(y)
Camada limite
dinâmica (0≤U<Uf)
Camada limite
térmica (θf<θ≤θs)
θ
α
θs
θf
U(y)
Quanto maior for Uf
menos espessas devem
ser as camadas limites
∆θ
∂θ
para escrever q = h c (θ s − θ f
Sendo q = −λ f
∂y y = 0
∂θ
∂θ
cot g (α ) =
− λf
a condutância deve ser:
∂y y = 0
∂y y = 0
hc =
Quando Uf aumenta α diminui e cotg(α) e hc aumentam
α
θs − θ f
)

19. TRANSMISSÃO DO CALOR: convecção (V)
Convecção ar-ar
Neste caso o ar entra no
espaço com a energia que
transporta do exterior:
Qin = m.cp.θe
θe
Qin
Qout
e, do contacto com o ar interior, à temperatura θi,
sai com a energia: Qout = m.cp.θi
A troca de calor resulta do
balanço líquido:
Q =Qout– Qin = m.cp.(θi - θe)
&
Q = ρ .c p .V(θ i − θ e )
Q = 0,34. R ph .ϑ (θi − θ e )
(W)
Conservação da massa:
min=mout= m=ρ.V
&
V = R ph .ϑ - caudal (m3/h)
ϑ - volume do espaço (m3)
Rph - nº de renovações/hora
ρ ≅1,2 kg/m3 ;cp≅ 1000 J/(kg.ºC)

20. TRANSMISSÃO DO CALOR: radiação (I)
A radiação térmica é a radiação electromagnética
emitida por um corpo causada pela temperatura a
que se encontra.
ESPECTRO ELECTROMAGNÉTICO
Radiação
Térmica
1 µm = 10-6 m
1 nm = 10-9 m
10-5 10-3 0.1
1 nm
Raios
Gama
UV
T
103
10
Infra
vermelho
0.4 0.5
105
1 mm
Micro
ondas
Raios
X
Violeta
Q
λ
107
λ (µm)
µ
1 metro
Ondas radio
Q = ε ⋅ σ ⋅ A ⋅ T4
Vermelho
0.6 0.7
A – área da superfície do corpo (m2);
Região visível
T - Temperatura absoluta (K);
A emissividade mede a eficiência com
σ- Constante de Stefan-Boltzmann (W/m2.K4);
que uma superfície emite radiação térmica.
ε- Emissividade da superfície (0≤ ε ≤ 1).

21. TRANSMISSÃO DO CALOR: radiação (II)
Quando a radiação (Q) incide sobre uma superfície
é em parte reflectida, transmitida e absorvida,
em percentagens ρ, τ e α , respectivamente.
A parcela da radiação que altera
a temperatura da superfície é a
radiação absorvida (Qabs=α⋅ inc).
α⋅Q
α⋅
Radiação
Incidente
Q1→2
→
Radiação
reflectida
2
Radiação
absorvida
A radiação incidente em 2 pode
Radiação
provir do sol ou de um objecto 1
transmitida
comum. Neste caso Qabs,2=α2 Q1→2=α2F1→2 ε1σ⋅A1T14.
α
σ⋅
→ α
→
F1→2 (Factor de forma) é fracção da energia
→
emitida pela superfície 1 que é interceptada por 2.

22. TRANSMISSÃO DO CALOR: radiação (III)
A troca de calor por radiação entre 2 superfícies
ocorre mesmo que não exista um meio físico a
separá-las. É um processo que ocorre no vácuo.
À semelhança da convecção e radiação, é
procurada uma expressão para a troca de energia
radiante entre duas superfícies que seja
directamente proporcional a uma diferença de
temperaturas, neste caso:
Q 2,1 = h r (2,1) . A1(θ2 − θ1 )
(W)
1
hr – Condutância térmica superficial
por radiação (W/m2ºC)
2

23. TRANSMISSÃO DO CALOR: radiação (IV)
Condutância térmica superficial por radiação
A energia emitida pela superfície I
TJ AJ
que atinge a superfície J é:
Q I → J = σ . ε I . FI → J . A I . TI4 ,
com
FI → J =
QI→J
QI
O cálculo de FI→J é um problema
→
puramente geométrico.
βJ
d
TI
βI
AI
Os factores de forma têm uma álgebra própria
obtida de diversas leis que se deduzem. Uma
delas é a lei da reciprocidade: A I .FI → J = A J . FJ → I
Para as situações correntes de térmica dos
edifícios os FI→J estão tabelados:

24. TRANSMISSÃO DO CALOR: radiação (V)
A energia absorvida por J vinda de I é: Q I − J = α J . Q I → J
Pela lei de Kirchoff da radiação, α = ε ,donde:
Q I − J = ε J . ε I . σ . FI → J . A I . TI4
Igualmente se deduz: Q J − I = ε I . ε J . σ . FJ → I . A J . TJ4
As trocas de calor líquidas são Q J , I = Q J − I − Q I − J ou seja,
(
Q J , I = ε I . ε J . σ FJ →I . A J . TJ4 − FI→J . A I . TI4
)
Recorrendo à lei da reciprocidade A I .FI → J = A J . FJ → I e
(
) (
(
)
)
efectuando a transformação: TJ4 − TI4 = TJ2 + TI2 (TJ + TI )(TJ − TI ) vem
Q J, I = h r ( J, I) A I (TJ − TI ), ou seja, Q J, I = h r ( J, I) A I (θ J − θ I ) , com
h r ( J , I) = ε I . ε J . σ . FI → J TJ2 + TI2 (TJ + TI )
A condutância depende das temperaturas das superfícies,
da sua emissividade e da forma como se inter-relacionam.

25. COEFICIENTE DE TRANSMISSÃO TÉRMICA
Hipóteses : - Regime permanente
- Fluxo unidireccional
Ext.
hsi - condutância térmica superficial interior
(inclui os efeitos da convecção e radiação interiores)
θe θse
hse - condutância térmica superficial exterior
(inclui os efeitos da convecção e radiação exteriores)
1
- condutância térmica da parede
Kp =
hse
λk
∑e
k k
θi
θsi
Q
Kp
Determinar o coeficiente U tal que Q possa ser
escrito em função de θi e θe: Q= U A (θi-θe)
Int.
hsi
Q= hsi A (θi-θsi)
Pela conservação da energia Q= Kp A (θsi-θse) donde
1
1
Q= hse A (θse-θe)
= R si +
+ R se
U
Kp
U - Coef. de transmissão térmica
Rsi=1/hsi
Rse=1/hse

26. PERDAS TÉRMICAS GLOBAIS - COEF. G (I)
Hipóteses:
Regime
permanente
θi > θe
θe
A - Área (m2)
L - Comprimento (m)
ϑ - Volume (m3)
QL
θe
QE
Perdas
em W
QE
θi
θe
ϑ
Perdas através dos elementos: Q E =
QL
NElem
∑U
Ek
A k (θ i − θ e )
k =1
Perdas através das ligações:
NLig
QL =
∑U
Lk
L k (θ i − θ e )
k =1
Perdas por renovação de ar: Q ar = ρ. c p . R ph . ϑ . (θi − θ e )

27. PERDAS TÉRMICAS GLOBAIS - COEF. G (II)
Coeficiente de Perdas Térmicas Globais (G1):
NElem
∑
G1 =
NLig
UEkAk +
k =1
∑U
Lk
Lk
(W/m3)
k =1
ϑ
Coeficiente G (inclui as perdas por ren. ar):
G = G1 + ρ. c p .R ph
(W/m3)
Consumo global horário duma instalação para
manter a temperatura interior num valor
constante (conforto):
Q = G . ϑ(θ i − θ e )
(W)

28. PERDAS TÉRMICAS GLOBAIS - COEF. G (III)
Consumo diário da instalação:
Q = G . ϑ(θ i − θe )× 24 (Wh)
θe - Temperatura média diária
Consumo anual da instalação:
N
(
)
Q = ∑ G . ϑ θ i − θe k × 24 (Wh) N - Número de dias da
estação de aquecimento
k =1
Graus-dias de aquecimento:
N
(
GD b = ∑ θ b − θe k
k =1
)
(ºC)
θ b - Temperatura base para a qual
é feito o somatório
Expressão final do método do coeficiente G:
Q = 0,024 × G . ϑ . GD b (kWh) O método não contempla os
ganhos solares
Uma forma de contornar este problema é utilizar os GD calculados
para uma temperatura base inferior à temperatura de conforto (~3ºC)

29. POTENCIA DUMA INSTALAÇÃO
Temperatura de projecto (θp)
θ (ºC)
É uma temperatura θ
i
cuja probabilidade
de ser ultrapassada
inferiormente é
θp
pequena (ex: 5%)
Potencia da instalação
θi (de conforto)
θe (exterior do local)
(θi -θe)
(θi -θp)
θe
Única altura em que a
Tempo (h)
instalação não satisfaz
as necessidades de aquecimento
O consumo horário da instalação é Q = G . ϑ(θ i − θ e )
A potência da instalação é P = G . ϑ(θ i − θ p )

30. NECESSIDADES ENERGÉTICAS
DE EDIFÍCIOS
METODOLGIA REGULAMENTAR
António Moret Rodrigues

31. MÉTODO REGULAMENTAR: aquecimento I
O balanço energético de um espaço para o caso
de temperatura controlada por termostato é:
Energia Auxiliar =Perdas através da Envolvente (condução,
convecção, radiação) – (Ganhos Solares + Ganhos Internos)
Necess. Úteis
Aquecimento
Nec. Brutas
Nic = Qt+Qv- Qgu
Ar exterior
Perdas por
pontes térmicas
Perdas pela
cobertura
Perdas por
ventilação
(convecção
ar-ar)
Ganhos
solares
Qt – Perdas por
condução através
da envolvente
Ar
exterior
Qv – Perdas por
renovação do ar
Qgu – Ganhos de calor úteis
Ar
interior
Perdas
pelo solo
Ganhos
internos
Ar
Perdas exterior
pelas
paredes
Energia auxiliar Nic

32. MÉTODO REGULAMENTAR: aquecimento II
PERDAS POR CONDUÇÃO PELA ENVOLVENTE
Qt=Qext+Qlna+Qpe+Qpt
Qext – perdas de calor pelas zonas correntes das paredes,
envidraçados, coberturas e pavimentos em contacto com
o exterior;
Qlna – perdas de calor pelas zonas correntes das paredes,
envidraçados e pavimentos em contacto com locais-não
aquecidos;
Qpe – perdas de calor pelos pavimentos e paredes em contacto
com o solo;
Qpt – perdas de calor pelas pontes térmicas existentes no edifício.

33. MÉTODO REGULAMENTAR: aquecimento III
PERDAS POR CONDUÇÃO PELA ENVOLVENTE
θi
θatm
θi
θa
θatm
Q=U ⋅A⋅ (θi - θa) (W)
U – Coeficiente de transmissão
térmica do elemento (W/m2ºC)
A – Área do elemento (m2)
- Envolvente em contacto
com o ar exterior
θa = θatm
- Envolvente em contacto
com o ar interior
θa = θi
- Envolvente em contacto
com local não aquecido
θa = θatm+ (1-τ)(θi-θatm)
0 <τ <1 (dependente do local)

34. MÉTODO REGULAMENTAR: aquecimento IV
PERDAS PELA ENVOLVENTE EM ZONA CORRENTE
ELEMENTOS EM CONTACTO COM O EXTERIOR
Em cada hora, as perdas são:
Qext = U·A·(θi - θatm)
(W)
U – coeficiente de transmissão térmica do elemento da envolvente (W/m2.ºC);
A – área do elemento da envolvente medida pelo interior (m2);
θi – temperatura do ar interior do edifício (ºC);
θatm – temperatura do ar exterior (ºC)
No final da estação de aquecimento, as perdas são:
Qext = 0,024·U·A·GD
GD – Graus-dia aquecimento.
(kWh)

35. MÉTODO REGULAMENTAR: aquecimento V
PERDAS POR PAREDES E PAVIMENTOS EM
CONTACTO COM O SOLO
Em cada hora e por grau centígrado, as perdas são:
Lpe = Σψi·Bj
(W/ºC)
ψi – coeficiente de transmissão térmica linear (W/m.ºC);
B – perímetro do pavimento ou o desenvolvimento da parede (m).
No final da estação de
aquecimento, as perdas são:
Qpe = 0,024·Lpe·GD (kWh)
GD – Graus-dia aquecimento.
ψpav ψpar
Parede em contacto com o solo
B
Pavimento em contacto
com o solo

36. MÉTODO REGULAMENTAR: aquecimento VI
PERDAS POR PONTES TÉRMICAS
Em cada hora, as perdas são:
Lpt = Σψi·Bj
(W/ºC)
ψi – coeficiente de transmissão térmica
linear da ponte térmica i (W/m.ºC);
Bi – desenvolvimento linear da
ponte térmica i (m).
Durante toda a estação de
aquecimento a energia necessária
para compensar as perdas lineares
é, para cada tipo de ponte térmicas da envolvente,
Qpt = 0,024⋅Lpt⋅GD
(kWh)
GD – Graus-dia aquecimento.

37. MÉTODO REGULAMENTAR: aquecimento VII
PERDAS DE CALOR POR RENOVAÇÃO DO AR
Em cada hora, as perdas são:
Qra = 0,34⋅Rph⋅Ap⋅Pd⋅(θi - θatm) (W/ºC)
Ap– área útil de pavimento (m2);
Pd – pé-direito (m);
θi – temperatura do ar interior do
edifício (ºC);
θatm – temperatura do ar exterior (ºC).
No final da estação de
aquecimento, as perdas são:
Qv = 0,024⋅(0,34⋅Rph⋅Ap⋅Pd)⋅GD
(kWh)
GD – Graus-dia aquecimento; Rph – Número de renovações horárias.

38. MÉTODO REGULAMENTAR: aquecimento VIII
GANHOS INTERNOS (Qi)
Os ganhos térmicos internos, incluem qualquer fonte de calor
situado no espaço a aquecer, excluindo o sistema de aquecimento,
nomeadamente:
- ganhos de calor associados ao metabolismo dos ocupantes;
- Calor dissipado nos equipamentos e nos dispositivos de
iluminação.
Os ganhos de calor de fontes internas durante toda a estação de
aquecimento são calculados por:
Qi = qi ·M·Ap×0,720
(kWh)
qi – ganhos térmicos internos médios por unidade de área útil de
pavimento (W/m2), numa base de 24h/dia, todos os dias do ano;
M – duração média da estação de aquecimento em meses;
Ap – área útil de pavimento (m2).

39. MÉTODO REGULAMENTAR: aquecimento IX
G=Gsul.X
Asomb
Ganhos Solares
GANHOS SOLARES (Qs)
Autil=Fs.Fg.Aenv
g⊥.Fw.Autil.G
Factor
solar
corrigido
O
+
N D J F M
Mês
- Ganhos solares úteis
- Ganhos solares brutos
X – factor de orientação;
Fs – factor de obstrução;
Fg – fracção envidraçada;
Fw – factor de correcção das propriedades do vidro;
g⊥ - factor solar (incidência normal da radiação).

40. MÉTODO REGULAMENTAR: aquecimento X
GANHOS SOLARES (Qs)
Na estação de aquecimento, os ganhos solares são calculados por:
Q s = G sul ∑ X j ∑ A snj .M
 n

j 

(kWh)
Gsul – energia solar média incidente numa superfície vertical orientada a sul de
área unitária durante a estação de aquecimento (kWh/m2.mês);
Xj – factor de orientação, para as diferentes exposições;
As – área efectiva colectora da radiação solar da superfície n que tem a
orientação j (m2);
j – índice que corresponde a cada uma das orientações.
Por sua vez, tem-se que: As = A.Fs.Fg.Fw.g⊥
A – área total do vão envidraçado (janela, incluindo vidro e caixilho);
Fs – factor de obstrução; Fw – factor de correcção das propriedades do vidro com
Fg – fracção envidraçada;
com o ângulo de incidência da radiação solar;
g ⊥ – factor solar do envidraçado, que inclui eventuais protecções solares.

41. MÉTODO REGULAMENTAR: aquecimento XI
GANHOS TÉRMICOS ÚTEIS (Qgu)
Na estação de aquecimento, os ganhos térmicos úteis são:
Qgu = η⋅Qg
(kWh)
Qg =Qi+Qs −Ganhos brutos;
Qi – Ganhos internos;
Qg – Ganhos solares;
η
η – Factor de utilização
1 − γa
η=
1 − γ a +1
a
η=
a +1
a=
se γ ≠1
se γ =1
γ
1,8 – edifícios com inércia térmica fraca;
Qg
Ganhos térmi cos brutos
γ=
=
2,6 – edifícios com inércia térmica média;
Nec. brutas de aquecimento Q t + Q v
4,2 – edifícios com inércia térmica forte.

42. MÉTODO REGULAMENTAR: aquecimento XII
INÉRCIA TÉRMICA
O termo Inércia térmica refere-se
à capacidade de um elemento
armazenar calor e só libertá-lo ao
fim certo tempo.
Desfasamento
temporal
θ
θmédia
A Inércia térmica pode ser
usada para absorver os ganhos
de calor durante o dia (reduzindo
a carga de arrefecimento) e
libertá-los à noite (reduzindo a
carga de aquecimento).
Amortecimento
térmico
Tempo
Parede
pesada
Superfície
interior
Superfície
exterior

43. MÉTODO REGULAMENTAR: aquecimento XIII
INÉRCIA TÉRMICA
Se as amplitudes térmicas diárias forem grandes, o dimensionamento
correcto da inércia térmica (amortecimento e desfasamento) permite
um melhor desempenho térmico das construções.
A inércia térmica depende da difusibilidade térmica α = k/(ρ.cp) ,
sendo k a condutibilidade térmica, ρ a densidade e cp o calor
específico do material.
∆qt
k
ρ
cp
∆qt+ϕ= µ.∆qt ϕ- tempo
de atraso
µ - factor de
amortecimento

44. MÉTODO REGULAMENTAR: aquecimento XIV
INÉRCIA TÉRMICA
Umas horas
depois ....
O isolamento térmico pelo
interior funciona como
tampa do reservatório de
armazenamento de calor
que constitui a massa da
construção.

45. MÉTODO REGULAMENTAR: arrefecimento I
Na estação quente, o balanço energético fornece:
Energia Auxiliar = Ganhos pela Envolvente (condução,
convecção, radiação) + Ganhos Solares + Ganhos Internos
As necessidades de arrefecimento são: Nvc= (1-η)⋅Qg
η⋅
Qg − Ganhos brutos;
Ar-sol
η – Factor de utilização (representa
a fracção dos ganhos
utilizáveis para o
conforto).
Ganhos
solares
Qg= Q1+ Q2 + Q3 + Q4
Q1- ganhos por condução
através da envolvente.
Q2 – ganhos solares através dos
envidraçados.
Q3 – ganhos por renovação do ar.
Q4 – ganhos internos.
(kWh)
Ganhos pela Ganhos por
cobertura
ventilação
(convecção ar-ar)
Ar
interior
Ganhos
pelas
paredes
Ganhos
internos
Ar -sol
Energia auxiliar Nvc

46. MÉTODO REGULAMENTAR: arrefecimento II
GANHOS POR CONDUÇÃO PELA ENVOLVENTE
Recorre-se ao conceito de temperatura ar-sol, que é temperatura
equivalente que traduz o efeito combinado da temperatura exterior
e da radiação solar:
 α⋅G 
 (W)
Q elemento = U ⋅ A(θar −sol − Ti ) = U ⋅ A(θar − Ti ) + U ⋅ A


α – coeficiente de absorção da superfície;
G – radiação solar instantânea.
 he 
G
Ao fim de 4 meses (122 dias):
 α ⋅ Ir
Q1 = 2,928 U ⋅ A(θ m − θ i ) + U ⋅ A
 h
 e
θm – temperatura média do ar;
Ir – Intensidade da radiação total.

 (kWh)


θs
θar
he
h e (θ ar −sol − θ s ) = h e (θ ar − θ s ) + α ⋅ G
Temperatura ar-sol: θ ar −sol = θ ar +
α.G
he

47. MÉTODO REGULAMENTAR: arrefecimento III
GANHOS SOLARES PELOS ENVIDRAÇADOS
O seu cálculo é semelhante à metodologia utilizada no Inverno:
Q 2 = ∑ Irj ∑ A s nj 

j 
 n

Ir – energia solar incidente nos vãos
O factor solar do envidraçado é
tomado com dispositivos de
sombreamento móveis activados
a 70% :
Q2=Qs1+Qs2=As1×Ir+As2×Ir
Q2=A×Fs.Fg.Fw.(0,7×g⊥+0,3×g⊥v).Ir
g ' .g
Vidro
g ⊥ = ⊥ ⊥v
simples:
0,85
com As = A.Fs.Fg.Fw.g⊥
(kWh)
Ir
Qs1
Qs2
Vidro g = g ' ⊥ .g ⊥ v
duplo: ⊥
0,75
As1=(0,7×A)Fs.Fg.Fw.g⊥
As2=(0,3×A)Fs.Fg.Fw.g⊥v

48. MÉTODO REGULAMENTAR: arrefecimento IV
GANHOS POR VENTILAÇÃO
Na realidade, dado que a temperatura média exterior
durante toda a estação de arrefecimento é sempre
inferior à temperatura interior de referência (25ºC), a
ventilação é, em média, uma perda, dada por:
Q 3 = 2,928 .(0,34.R ph .A p .Pd ).(θ m − θ i )
(kWh)
GANHOS INTERNOS
A metodologia de cálculo é semelhante à da estação de
aquecimento, vindo:
Q 4 = 2,928 . q i .A p
(kWh)