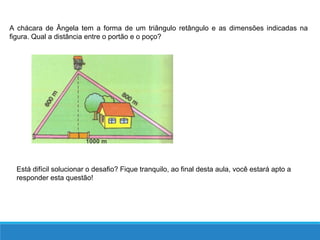
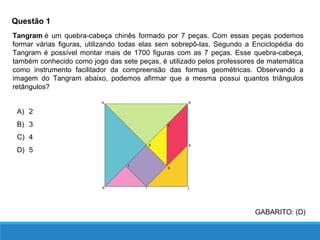
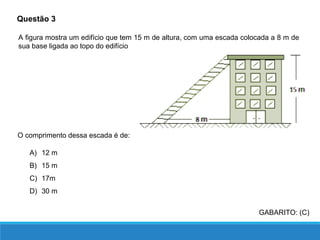
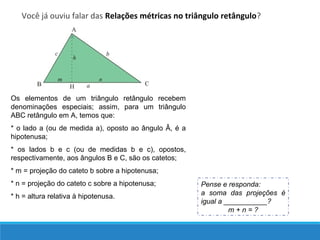
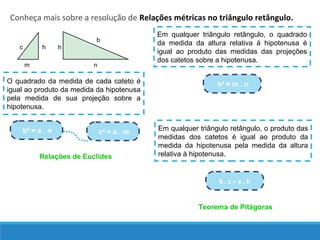
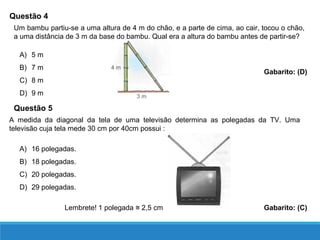
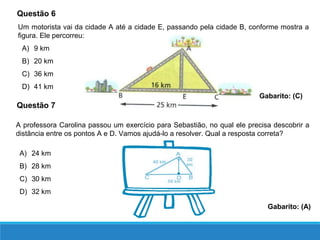
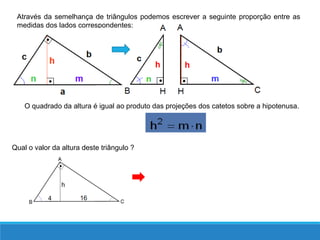
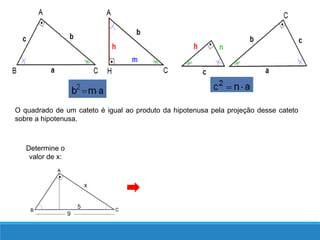
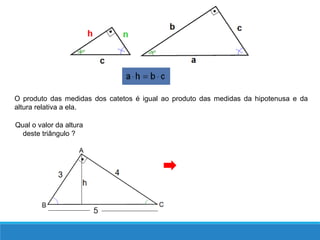
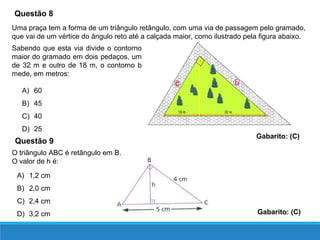
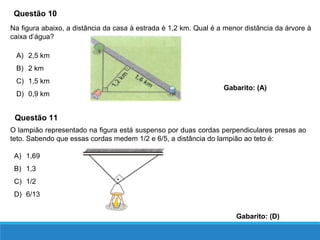
O documento descreve as relações métricas em triângulos retângulos, definindo os elementos do triângulo (hipotenusa, catetos, altura relativa à hipotenusa e projeções dos catetos) e apresentando as principais relações entre esses elementos, como o Teorema de Pitágoras e a igualdade entre o quadrado da altura e o produto das projeções.

1. a: hipotenusa
b: maior cateto
c: menor cateto
h: altura relativa à hipotenusa
m: projeção do cateto b
n: projeção do cateto c
Relações métricas no triângulo
retângulo:
Identificar as relações métricas nos triângulos retângulos e aplicá-las na
resolução de problemas;
O Teorema de Pitágoras relaciona os
catetos com a hipotenusa.
Como fica a fórmula?

2. Está difícil solucionar o desafio? Fique tranquilo, ao final desta aula, você estará apto a
responder esta questão!
A chácara de Ângela tem a forma de um triângulo retângulo e as dimensões indicadas na
figura. Qual a distância entre o portão e o poço?
1000 m

3. Relações métricas no triângulo retângulo...
As construções das pirâmides e dos templos pela
civilização egípcia e babilônica são o testemunho
mais antigo de um conhecimento sistemático da
geometria. Nessas construções nota-se a presença de
ângulos retos e linhas retas perpendiculares entre si.
De acordo com a história os antigos egípcios
utilizavam o triângulo retângulo para construir os
ângulos retos.
Hoje em dia os operários da construção civil usam
linhas na demarcação de terrenos e na construção de
casas. Esses profissionais também utilizam esquadros
para conferir cantos retos.
Assista ao vídeo abaixo e conheça um
pouco mais sobre o assunto.
http://www.youtube.com/watch?v=hVpbAacwD-M

4. Questão 1
Tangram é um quebra-cabeça chinês formado por 7 peças. Com essas peças podemos
formar várias figuras, utilizando todas elas sem sobrepô-las. Segundo a Enciclopédia do
Tangram é possível montar mais de 1700 figuras com as 7 peças. Esse quebra-cabeça,
também conhecido como jogo das sete peças, é utilizado pelos professores de matemática
como instrumento facilitador da compreensão das formas geométricas. Observando a
imagem do Tangram abaixo, podemos afirmar que a mesma possui quantos triângulos
retângulos?
A) 2
B) 3
C) 4
D) 5
GABARITO: (D)

5. Questão 2
As construções das pirâmides e templos pelas civilizações egípcia e babilônica são o
testemunho mais antigo de um conhecimento sistemático da Geometria. Contudo, muitas
outras civilizações antigas possuíam conhecimentos de natureza geométrica, desde a
Babilônia até a China, passando pela civilização hindu. Os babilônios tinham
conhecimentos matemáticos que provinham da agrimensura e comércio e a civilização
hindu conhecia o teorema sobre o quadrado da hipotenusa de um ___________________.
Qual figura geométrica completa o texto acima?
A)Losango
B)Paralelogramo
C)Quadrado
D)Triângulo retângulo
GABARITO: (D)

6. Questão 3
GABARITO: (C)
A figura mostra um edifício que tem 15 m de altura, com uma escada colocada a 8 m de
sua base ligada ao topo do edifício
O comprimento dessa escada é de:
A) 12 m
B) 15 m
C) 17m
D) 30 m

7. Você já ouviu falar das Relações métricas no triângulo retângulo?
Os elementos de um triângulo retângulo recebem
denominações especiais; assim, para um triângulo
ABC retângulo em A, temos que:
* o lado a (ou de medida a), oposto ao ângulo Â, é a
hipotenusa;
* os lados b e c (ou de medidas b e c), opostos,
respectivamente, aos ângulos B e C, são os catetos;
* m = projeção do cateto b sobre a hipotenusa;
* n = projeção do cateto c sobre a hipotenusa;
* h = altura relativa à hipotenusa.
Pense e responda:
a soma das projeções é
igual a ___________?
m + n = ?

8. Conheça mais sobre a resolução de Relações métricas no triângulo retângulo.
Em qualquer triângulo retângulo, o quadrado
da medida da altura relativa à hipotenusa é
igual ao produto das medidas das projeções
dos catetos sobre a hipotenusa.
h² = m . nO quadrado da medida de cada cateto é
igual ao produto da medida da hipotenusa
pela medida de sua projeção sobre a
hipotenusa.
c² = a . mb² = a . n Em qualquer triângulo retângulo, o produto das
medidas dos catetos é igual ao produto da
medida da hipotenusa pela medida da altura
relativa à hipotenusa.
b . c = a . h
nm
c h h
b
Relações de Euclides
Teorema de Pitágoras

9. Questão 4
A) 5 m
B) 7 m
C) 8 m
D) 9 m
Gabarito: (D)
Um bambu partiu-se a uma altura de 4 m do chão, e a parte de cima, ao cair, tocou o chão,
a uma distância de 3 m da base do bambu. Qual era a altura do bambu antes de partir-se?
Questão 5
A medida da diagonal da tela de uma televisão determina as polegadas da TV. Uma
televisão cuja tela mede 30 cm por 40cm possui :
A) 16 polegadas.
B) 18 polegadas.
C) 20 polegadas.
D) 29 polegadas.
Lembrete! 1 polegada 2,5 cm≅ Gabarito: (C)

10. Questão 6
Um motorista vai da cidade A até a cidade E, passando pela cidade B, conforme mostra a
figura. Ele percorreu:
A) 9 km
B) 20 km
C) 36 km
D) 41 km
Gabarito: (C)
Questão 7
A professora Carolina passou um exercício para Sebastião, no qual ele precisa descobrir a
distância entre os pontos A e D. Vamos ajudá-lo a resolver. Qual a resposta correta?
A) 24 km
B) 28 km
C) 30 km
D) 32 km
Gabarito: (A)

11. O quadrado da altura é igual ao produto das projeções dos catetos sobre a hipotenusa.
Através da semelhança de triângulos podemos escrever a seguinte proporção entre as
medidas dos lados correspondentes:
Qual o valor da altura deste triângulo ?

12. O quadrado de um cateto é igual ao produto da hipotenusa pela projeção desse cateto
sobre a hipotenusa.
Determine o
valor de x:

13. O produto das medidas dos catetos é igual ao produto das medidas da hipotenusa e da
altura relativa a ela.
Qual o valor da altura
deste triângulo ?

14. Questão 8
Uma praça tem a forma de um triângulo retângulo, com uma via de passagem pelo gramado,
que vai de um vértice do ângulo reto até a calçada maior, como ilustrado pela figura abaixo.
Sabendo que esta via divide o contorno
maior do gramado em dois pedaços, um
de 32 m e outro de 18 m, o contorno b
mede, em metros:
A) 60
B) 45
C) 40
D) 25
Gabarito: (C)
O triângulo ABC é retângulo em B.
O valor de h é:
Questão 9
A) 1,2 cm
B) 2,0 cm
C) 2,4 cm
D) 3,2 cm Gabarito: (C)

15. Questão 10
Na figura abaixo, a distância da casa à estrada é 1,2 km. Qual é a menor distância da árvore à
caixa d’água?
A) 2,5 km
B) 2 km
C) 1,5 km
D) 0,9 km
Gabarito: (A)
O lampião representado na figura está suspenso por duas cordas perpendiculares presas ao
teto. Sabendo que essas cordas medem 1/2 e 6/5, a distância do lampião ao teto é:
A) 1,69
B) 1,3
C) 1/2
D) 6/13
Gabarito: (D)
Questão 11