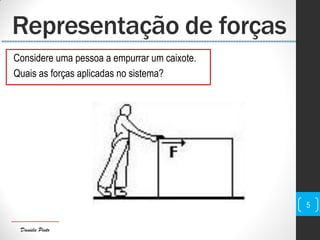
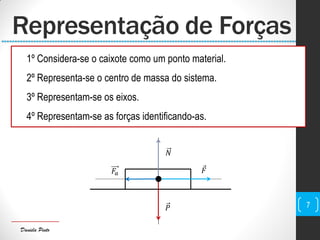
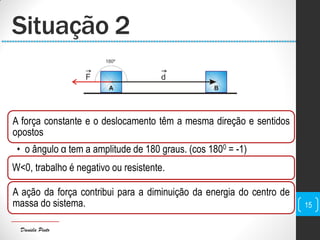
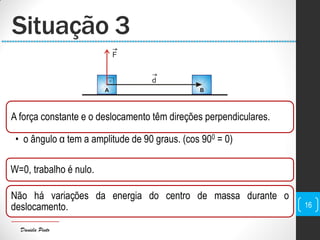
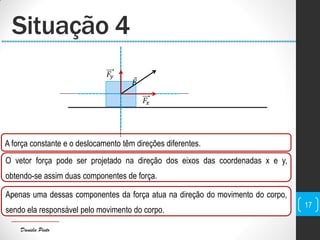
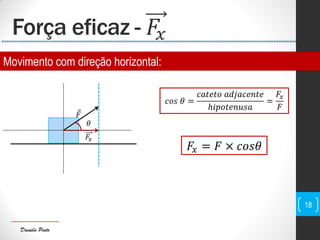
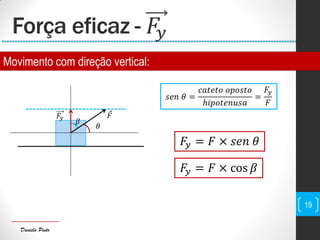
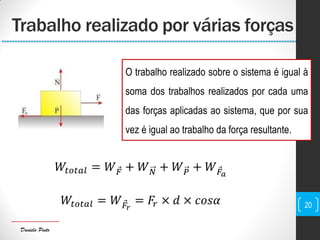
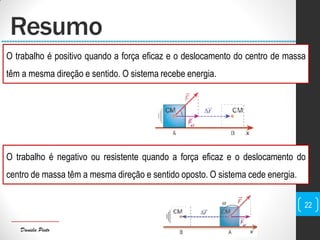
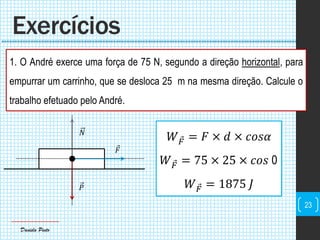
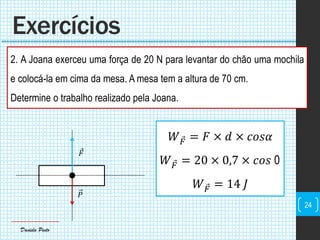
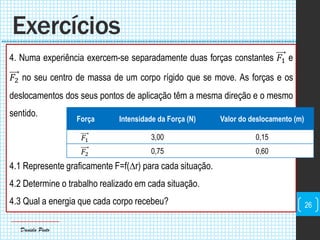
O documento discute conceitos fundamentais de mecânica, incluindo centro de massa, forças, trabalho e energia. Explica que o trabalho é a transferência de energia através da ação de uma força e pode ser positivo, negativo ou nulo dependendo da direção da força em relação ao deslocamento.

1. Trabalho de uma força

2. Daniela Pinto
Sistema mecânico
• Sistema físico em estudo.
• Estuda-se o movimento.
• Consideram-se, apenas, as quantidades de energia
útil e dissipada associadas ao movimento.
• Despreza-se as variações de energia interna.
2

3. Daniela Pinto
Centro de massa, CM
Quando os corpos rígidos, indeformáveis, não experimentam qualquer
variação de energia interna, podem ser aproximados a partículas
materiais representadas pelo seu centro de massa.
v

v
v

v

v
 CM
Todos os pontos têm a mesma velocidade e
descrevem trajetórias paralelas – translação pura.
3

4. Daniela Pinto
Características do CM
É representado por um ponto que representa o corpo rígido, indeformável;
No sistema só ocorrem transferências de energia como trabalho;
Tem uma massa igual à massa do sistema físico;
Tem velocidade igual à velocidade de cada uma das partículas do corpo;
O sistema só tem movimento de translação pura;
As forças que atuam no sistema provocam o mesmo efeito quando aplicadas
no CM; 4

5. Daniela Pinto
Representação de forças
Considere uma pessoa a empurrar um caixote.
Quais as forças aplicadas no sistema?
5

6. Daniela Pinto
Caracterização de uma força
As forças
que atuam
sobre um
corpo têm
associado a
si:
• Direção- linha de ação da grandeza (exemplo,
horizontal, vertical).
• Sentido- orientação do vetor para uma dada
direção (exemplo, da esquerda para a direita e
de baixo para cima).
• Intensidade- valor numérico (N).
• Ponto de aplicação- ponto onde a grandeza
atua.
6

7. Daniela Pinto
Representação de Forças
𝐹
𝑃
𝐹𝑎
𝑁
1º Considera-se o caixote como um ponto material.
2º Representa-se o centro de massa do sistema.
3º Representam-se os eixos.
4º Representam-se as forças identificando-as.
7

8. Daniela Pinto
Cálculo da força resultante
As forças aplicadas no centro de massa são:
𝐹 − força aplicada no corpo
𝐹𝑔 − força gravítica exercida pela Terra sobre o caixote (peso de um corpo - 𝑃)
𝑁 ou 𝑅 𝑁 − reação normal da superfície sobre o corpo
𝐹𝑎 − força de atrito sobre o caixote
𝐹𝑅 = 𝐹 + 𝐹𝑔 + 𝑁 + 𝐹𝑎
𝐹𝑔 + 𝑁 = 0 logo 𝐹𝑅 = 𝐹 + 𝐹𝑎 8

9. Daniela Pinto
Força Resultante
Força Resultante, é o que resulta de todas as forças aplicadas num
corpo, e pode ser expressa por:
𝑭 𝒓 = 𝒎. 𝒂
𝐹𝑟►é a força resultante, expressa em newtons (N);
𝑚►é a massa do corpo, expressa em quilogramas (kg);
𝑎 ►é a aceleração, medida em (m/s2).
9

10. Daniela Pinto
P ►peso (N)
m ►massa do corpo (kg)
g ►valor da aceleração da gravidade (ms-2), constante num dado
local da superfície da Terra.
Peso de um corpo
10
𝑃 = 𝑚 × 𝑔

11. Daniela Pinto
Atuação de uma força constante
11

12. Daniela Pinto
Trabalho realizado por uma força constante
12
Um joule é o trabalho realizado por uma força constante de
intensidade um newton, que atua na direção e sentido do deslocamento,
quando o seu ponto de aplicação se desloca de um metro.
Trabalho é uma forma de transferência de energia mas, para que ocorra é
necessário a atuação de uma força. A unidade SI de trabalho é o Joule, J.
d
F


13. Daniela Pinto
𝛼
O trabalho é uma grandeza escalar que depende:
13
Da intensidade da força constante que atua no corpo;
Do valor do deslocamento do ponto de aplicação dessa força;
Do ângulo α que fazem entre si as direções dos vetores força e deslocamento.
𝑊 𝐹 = 𝐹 × 𝑑 = 𝐹 × 𝑑 × 𝑐𝑜𝑠𝛼
F

 x
d
m
O trabalho é uma grandeza escalar
A unidade de trabalho no SI é o joule (J)

14. Daniela Pinto
Situação 1
14
A força constante e o deslocamento têm a mesma direção e o mesmo
sentido
• o ângulo α tem a amplitude de zero graus. (cos 00 = 1)
W>0, trabalho é positivo, potente ou motor.
A ação da força contribui para o aumento da energia do centro de
massa do sistema (máxima eficácia).

15. Daniela Pinto
Situação 2
15
A força constante e o deslocamento têm a mesma direção e sentidos
opostos
• o ângulo α tem a amplitude de 180 graus. (cos 1800 = -1)
W<0, trabalho é negativo ou resistente.
A ação da força contribui para a diminuição da energia do centro de
massa do sistema.

16. Daniela Pinto
Situação 3
16
A força constante e o deslocamento têm direções perpendiculares.
• o ângulo α tem a amplitude de 90 graus. (cos 900 = 0)
W=0, trabalho é nulo.
Não há variações da energia do centro de massa durante o
deslocamento.

17. Daniela Pinto
Situação 4
17
A força constante e o deslocamento têm direções diferentes.
O vetor força pode ser projetado na direção dos eixos das coordenadas x e y,
obtendo-se assim duas componentes de força.
Apenas uma dessas componentes da força atua na direção do movimento do corpo,
sendo ela responsável pelo movimento do corpo.
𝐹
𝐹𝑥
𝐹𝑦

18. Daniela Pinto
Força eficaz - 𝐹𝑥
18
𝑐𝑜𝑠 𝜃 =
𝑐𝑎𝑡𝑒𝑡𝑜 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝑒
ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎
=
𝐹𝑥
𝐹
𝐹𝑥 = 𝐹 × 𝑐𝑜𝑠𝜃
𝐹
𝐹𝑥
𝜃
Movimento com direção horizontal:

19. Daniela Pinto
Força eficaz - 𝐹𝑦
19
Movimento com direção vertical:
𝐹𝐹𝑦
𝑠𝑒𝑛 𝜃 =
𝑐𝑎𝑡𝑒𝑡𝑜 𝑜𝑝𝑜𝑠𝑡𝑜
ℎ𝑖𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑎
=
𝐹𝑦
𝐹
𝜃
𝐹𝑦 = 𝐹 × 𝑠𝑒𝑛 𝜃
𝛽
𝐹𝑦 = 𝐹 × cos 𝛽

20. Daniela Pinto
O trabalho realizado sobre o sistema é igual à
soma dos trabalhos realizados por cada uma
das forças aplicadas ao sistema, que por sua
vez é igual ao trabalho da força resultante.
Trabalho realizado por várias forças
20
𝑊𝑡𝑜𝑡𝑎𝑙 = 𝑊 𝐹 + 𝑊 𝑁 + 𝑊 𝑃 + 𝑊 𝐹𝑎
𝑊𝑡𝑜𝑡𝑎𝑙 = 𝑊 𝐹𝑟
= 𝐹𝑟 × 𝑑 × 𝑐𝑜𝑠𝛼

21. Daniela Pinto
Gráfico
A área do gráfico permite calcular o trabalho realizado por uma força
constante.
21

22. Daniela Pinto
Resumo
O trabalho é positivo quando a força eficaz e o deslocamento do centro de massa
têm a mesma direção e sentido. O sistema recebe energia.
O trabalho é negativo ou resistente quando a força eficaz e o deslocamento do
centro de massa têm a mesma direção e sentido oposto. O sistema cede energia.
22

23. Daniela Pinto
1. O André exerce uma força de 75 N, segundo a direção horizontal, para
empurrar um carrinho, que se desloca 25 m na mesma direção. Calcule o
trabalho efetuado pelo André.
Exercícios
23
𝐹
𝑃
𝑁
𝑊 𝐹 = 𝐹 × 𝑑 × 𝑐𝑜𝑠𝛼
𝑊 𝐹 = 75 × 25 × 𝑐𝑜𝑠 0
𝑊 𝐹 = 1875 𝐽

24. Daniela Pinto
2. A Joana exerceu uma força de 20 N para levantar do chão uma mochila
e colocá-la em cima da mesa. A mesa tem a altura de 70 cm.
Determine o trabalho realizado pela Joana.
Exercícios
24
𝑃
𝐹
𝑊 𝐹 = 𝐹 × 𝑑 × 𝑐𝑜𝑠𝛼
𝑊 𝐹 = 20 × 0,7 × 𝑐𝑜𝑠 0
𝑊 𝐹 = 14 𝐽

25. Daniela Pinto
3. O senhor Joaquim empurra um móvel sobre uma superfície horizontal,
exercendo uma força paralela ao plano de apoio, de módulo 80 N,
efetuando um percurso de 3,0 m.
3.1 Represente o móvel e todas as forças aplicada. Despreze o atrito.
3.2 Determine o trabalho realizado por cada uma das forças aplicadas no
corpo.
Exercícios
25

26. Daniela Pinto
4. Numa experiência exercem-se separadamente duas forças constantes 𝐹1 e
𝐹2 no seu centro de massa de um corpo rígido que se move. As forças e os
deslocamentos dos seus pontos de aplicação têm a mesma direção e o mesmo
sentido.
4.1 Represente graficamente F=f(r) para cada situação.
4.2 Determine o trabalho realizado em cada situação.
4.3 Qual a energia que cada corpo recebeu?
Exercícios
Força Intensidade da Força (N) Valor do deslocamento (m)
𝐹1 3,00 0,15
𝐹2 0,75 0,60
26