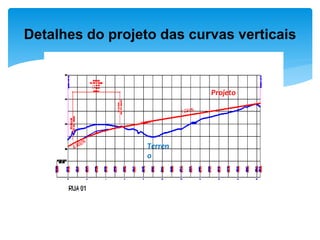
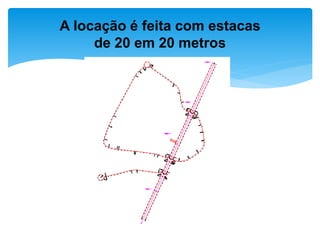
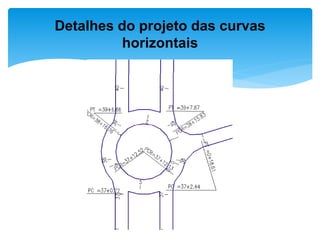
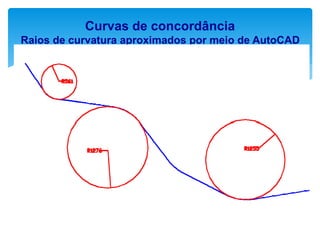
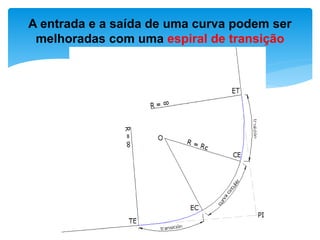
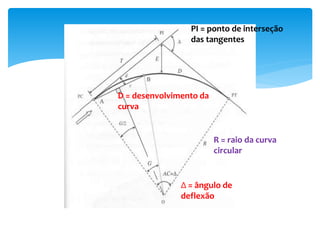
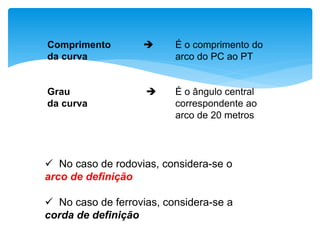
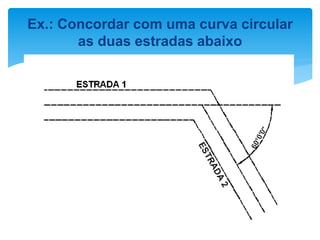
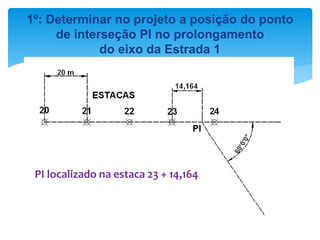
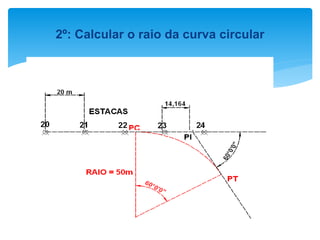
O documento discute projetos de curvas horizontais para locação de vias, incluindo definições de termos como raio, grau e comprimento de curva. Exemplos demonstram como calcular parâmetros de curvas como raio, grau e localização de estacas usando fórmulas com base em ângulo de deflexão e desenvolvimento.

1. CURVAS HORIZONTAIS PARA
LOCAÇÃO DE VIAS
Geomática II GEO 018
Prof. Rachel Russo

2. Curvas de Nível

3. Projeto do traçado de vias

4. Detalhes do projeto das curvas verticais
Terren
o
Projeto

5. A locação é feita com estacas
de 20 em 20 metros

6. Detalhes do projeto das curvas
horizontais

7.  Na mudança de direção em uma via, deve ser
projetada uma curva de concordância que seja
tangente aos eixos das duas direções
Curvas de concordância
 Tipicamente o eixo da curva de concordância é um arco
de raio constante (curva circular)
 O raio das curvas depende do uso da via:
 Via Urbana, Rodovia, Ferrovia
Curvas Horizontais de Concordância

8. Ex.: Trecho rodovia
São Carlos – Dourado
Curvas horizontais
Levantamento feito com GPS de
navegação

9. Curvas de concordância
Raios de curvatura aproximados por meio de AutoCAD

10. Geometria da curva circular
A geometria de uma estrada é definida pelo traçado
do eixo em planta e pelos perfis longitudinal e
transversal. De maneira simplificada, o traçado em
planta é composto de trechos retos concordados
por curvas horizontais
Em princípio, uma estrada deve ter o traçado mais
curto possível. Porém, ligeiras deflexões, quando
necessárias, podem harmonizar o traçado da
estrada com a topografia local
Classe da rodovia  impactos ambientais
maiores/menores

11. Ex.: Curva na Rodovia SP 310

12. Ex.: Curva na Marginal

13. A entrada e a saída de uma curva podem ser
melhoradas com uma espiral de transição

14. PI = ponto de interseção
das tangentes
D = desenvolvimento da
curva
R = raio da curva
circular
Δ = ângulo de
deflexão

15. Definições
PC = ponto de curva ou ponto de curvatura
PT = ponto de tangente ou ponto de tangência
PI = ponto de interseção das tangentes
D = desenvolvimento da curva
Δ = ângulo de deflexão
AC = ângulo central da curva = Deflexão
R = raio da curva circular
T = tangente externa
O = Centro da curva
E = afastamento
G = grau da curva
c = corda
d = deflexão sobre a tangente

16. Comprimento  É o comprimento do
da curva arco do PC ao PT
Grau  É o ângulo central
da curva correspondente ao
arco de 20 metros
 No caso de rodovias, considera-se o
arco de definição
 No caso de ferrovias, considera-se a
corda de definição

17. R = 3600
 G
G em graus sexagesimais
R = 4000
 G
G em grados (centesimais)
d20 = G/2
T = R tg AC
2
D = AC 20 m
G
D =  R AC
180
Fórmulas Básicas

18.  O estaqueamento é feito de 20 em 20 m
 Portanto: 4 estacas = 80 m
 Alguns casos tem estacas de 50 em 50 m, ou 10 em
10 m
Estacas principais:
EST PC = EST PI – T
EST PT = EST PC + D
Deflexão para 20 m = d20 = G/2
As demais deflexões são proporcionais aos respectivos
arcos
ESTACAS

19. Ex.: Concordar com uma curva circular
as duas estradas abaixo

20. 1º: Determinar no projeto a posição do ponto
de interseção PI no prolongamento
do eixo da Estrada 1
PI localizado na estaca 23 + 14,164

21. 2º: Calcular o raio da curva circular

22. 3º: Calcular a posição do ponto PC
T = R tg (AC/2) = 50 tg (30o00’00”) = 28,868 m = 1 + 8,868 m
PC = PI - T = 23 + 14,164 m – (1 + 8,868 m) = 22 + 5,296 m
4º: Locação da 1ª estaca na curva
O grau desta curva para 20 m = G = 3600/( . 50)
G = 22,9183º
A primeira estaca na curva se encontra na distância
l:
l = 20,000 – 5,296 = 14,704 m do PC

23. 1) Calcular o raio de uma curva de 200 m de
comprimento entre as duas tangentes cujos
azimutes são:
 Az1 = 142o 32’
 Az2 = 153o 02’
2) Calcular o raio, o grau e o comprimento de
curva para o seguinte trecho de via:
Az inicial = 342o 31’
Az final = 8o 22’ T = 110 m
Exercícios

24. 3) Calcular e preparar a curva horizontal circular
para locação pelo método das deflexões:
G = 8o AC = 44o 00’ à esquerda
EST PI = 214 + 5,50
Az inicial = 0o 00’
Estaqueamento de 10 em 10 m
Exercícios