Este documento descreve os conceitos fundamentais de circuitos elétricos em corrente alternada (CA) em paralelo. Resume os principais parâmetros a serem estudados neste tipo de circuito, como a tensão e corrente em todos os elementos. Explica como a admitância, corrente, potência e outros parâmetros se comportam em circuitos RLC em paralelo, incluindo o conceito importante de ressonância. Fornece exemplos numéricos para ilustrar como calcular essas grandezas em circuitos RC e RL.

1. Análise de circuitos elétricos CC e CA Pedro Barros Neto
17 - Circuito CA em paralelo (Fig. 17 – 01)
17.1 - Parâmetros a serem estudados neste tipo de circuito:
Circuito em paralelo é um divisor de corrente, com a mesma tensão em todos os elementos.
Se o módulo da tensão total estiver como referência de fase V ∠0° → ω t =0 rad , isso significa
que a condutância G , sua queda de tensão VdG e a potência eficaz P , estarão
vetorialmente na mesma reta suporte do vetor do módulo da tensão V , sobre o eixo Real
positivo do plano complexo, enquanto que, a susceptância indutiva BL , sua queda de tensão
VdBL e a potência reativa QL são representadas nos quadrantes − j , e que a susceptância
capacitiva BC , sua queda de tensão VdBC e a potência reativa QC , ficam nos quadrantes
+ j . Notar que houve uma inversão das grandezas imaginárias, em relação ao circuito em
série.
Nos tópicos seguintes trataremos da tensão com “fase zero”, sobre o eixo Real positivo, exceto nos
casos em que for dado um ângulo diferente de fase inicial da tensão. As tensões e correntes com
valores RMS.
17.2 – Triângulo da admitância (Fig. 17 – 02)
Susceptâncias: unidade de medida Siemens S .
Capacitiva jBC =
1
XC
e indutiva −jBL =
1
XL
.
A admitância complexa: unidade de medida Siemens (S)
é dada por Y =
1
Z
ou, em função do módulo da tensão RMS e
da corrente complexa Y =
I
V
.
Na forma retangular Y =G + J BC ou Y =G −J BL .
1

2. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Na forma polar: Módulo da admitância Y = √G
2
+ BEQ
2
.
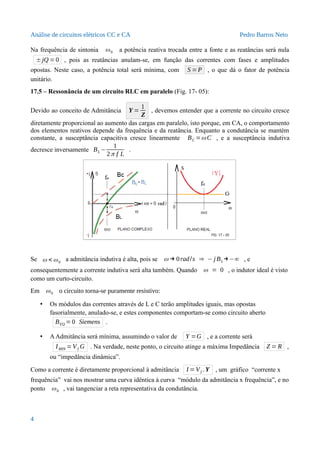
Predominância indutiva: Y =Y ∠m .d. p.(−ϕ ) .
Predominância capacitiva: Y =Y ∠ ϕ .
Com o módulo da admitância poderemos ter: Y =Ycosϕ ± j(Y senϕ ) onde G =Y cosϕ é a
parte real e BL = j(Y senϕ ) ou BC =−j(Y senϕ ) a parte Imaginária.
Comparação das relações fasoriais nos circuitos em série e paralelo:
Ângulo da defasagem entre a tensão e a corrente:
• Circuito RL . ϕ =tg
−1
[− j BL
G ]
• Circuito RC . ϕ =tg
−1
[j BC
G ]
• Circuito RLC ϕ =tg−1
[±j BEQ
G ] .
Como consequência, teremos: cosϕ =
G
Y
senϕ L =
−jBL
Y
senϕ C =
jBC
Y
.
Para ângulo negativo (predominância indutiva), converter para a “menor determinação positiva”:
m.d . p. (−ϕ )=−ϕ + 360° .
17.2 – Triângulo das correntes (Fig. 17-03):
Como adotamos o módulo da tensão como referência fasorial, a corrente complexa será dada plela
Lei de Ohm I =V .YEQ , mostrando que a corrente cresce diretamente proporcional à
admitância complexa do circuito.
A corrente total de um circuito em paralelo é a soma das
correntes de cada braço. Se o circuito tiver “n” braços, pela LCK,
teremos : IEQ = I1 + I2 + I3 + ….In .
LCK→IR+( jIC−jIL)= I ou I = IR± j Ireativo onde
Ireativo =( jIC− jI L) é a corrente resultante dos elementos
reativos opostos.
Corrente no resistor em paralelo, pela Lei de Ohm: IR =
V
R
.
2

3. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Corrente no capacitor em paralelo: IC =
V
jXC
.
Corrente instantânea no capacitor, em função da capacitância e a derivada da tensão instantânea
(relação constitutiva): i(t)=C[dv(t)
dt ] .
Corrente no indutor em paralelo: IL =
V
−jXL
.
Corrente instantânea no indutor, em função da capacitância e a integral da tensão instantânea
(relação constitutiva): i(t)=
1
L
∫
0
t
v(t)dt .
Módulo da corrente total: I =√(IR)
2
+(Ireativo)
2
.
17.4 – Triângulo das Potências na carga (Fig. 17- 04):
Todas as fórmulas de potência dos circuitos em série são válidas
para os circuitos em paralelo.
Potência total na forma retangular S= PG ± jQEQ , com:
PG =V ²G ou PG =
I
2
G
e Q =V
2
(± j BEQ) ou
Q =
I
2
± j BEQ
. Módulo da potência total ou potência aparente
S =√P
2
+(±j QEQ)
2
.
Potência total na forma polar S=S ∠ϕ para carga capacitiva e S=S ∠m.d . p.(−ϕ ) para
carga indutiva.
Fator de potência FP=cosϕ ou FP=
P
S
.
Em função da frequência do gerador, num circuito RCL em paralelo, teremos:
Se f → 0 a máxima potência reativa é trocada entre o indutor e o gerador; se f →+∞ a
máxima potência reativa é trocada entre o capacitor e o gerador e, nos dois casos, a potência
trocada entre a fonte e as reatâncias será máxima S= P± jQ , onde P é a potência média
dissipada no resistor P=
V
2
R
ou P=I2
R ou P=VI cosϕ .
3

4. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Na frequência de sintonia ω0 a potência reativa trocada entre a fonte e as reatâncias será nula
± jQ =0 , pois as reatâncias anulam-se, em função das correntes com fases e amplitudes
opostas. Neste caso, a potência total será mínima, com S =P , o que dá o fator de potência
unitário.
17.5 – Ressonância de um circuito RLC em paralelo (Fig. 17- 05):
Devido ao conceito de Admitância Y =
1
Z
, devemos entender que a corrente no circuito cresce
diretamente proporcional ao aumento das cargas em paralelo, isto porque, em CA, o comportamento
dos elementos reativos depende da frequência e da reatância. Enquanto a condutância se mantém
constante, a susceptância capacitiva cresce linearmente BC =ω C , e a susceptância indutiva
decresce inversamente BL −
1
2π f L
.
Se ω < ω0
a admitância indutiva é alta, pois se ω → 0rad/s ⇒ − j BL→−∞ , e
consequentemente a corrente indutiva será alta também. Quando ω = 0 , o indutor ideal é visto
como um curto-circuito.
Em ω0 o circuito torna-se puramente resistivo:
• Os módulos das correntes através de L e C terão amplitudes iguais, mas opostas
fasorialmente, anulado-se, e estes componentes comportam-se como circuito aberto
BEQ =0 Siemens .
• AAdmitância será mínima, assumindo o valor de Y =G , e a corrente será
IMIN =Vf G . Na verdade, neste ponto, o circuito atinge a máxima Impedância Z = R ,
ou “impedância dinâmica”.
Como a corrente é diretamente proporcional à admitância I =Vf .Y , um gráfico “corrente x
frequência” vai nos mostrar uma curva idêntica à curva “módulo da admitância x frequência”, e no
ponto ω0 , vai tangenciar a reta representativa da condutância.
4

5. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Se ω >ω0 , a admitância capacitiva é alta, pois quando ω → ∞rad/s ⇒ +JBC →+∞ , e
consequentemente a corrente capacitiva será alta também. Quando ω → ∞ , o capacitor ideal
tende para um curto-circuito.
• Na frequência de ressonância teremos XL = XC ω0 L=
1
ω0C
ω0
2
=
1
LC
ou
ω0 =
1
√LC
rad /s .
Fator de qualidade “Q”
Já vimos no capítulo 16 (circuitos CA em série) que o fator de qualidade Q de um circuito
ressonante é a razão entre a energia armazenada nos elementos reativos e a energia dissipada no
resistor em série, a cada ciclo: Q =
U X
U R
(16.04). A definição já sugere que, se as reatâncias
LC estão em paralelo, tem que haver um resistor em série RS (fig. 17 - 06), além do que, a
expressão do fator Q será invertida em relação à expressão vista quando temos LC em série: e
Q =Rω0C e Q =
R
ω0 L
ou Q =R
√C
L
.
O fator Q é visto num gráfico “impedância x
frequência” nas vizinhanças de ω0 , (fig.17 – 07)
como a curva do módulo da impedância, com vértice
para cima, centrado em ω0 , e ordenada Z = R
, ou seja, ponto da impedância máxima.
Uma resistência alta em série produzirá um Q
maior, cujo gráfico será um pico elevado e delgado,
com a banda de atenuação mais estreita, tornando o
circuito mais seletivo, enquanto que uma resistência
mais baixa vai produzir um Q menor, cujo gráfico
será uma curva com pico baixo e achatado, com uma
banda de atenuação mais larga e menos seletiva.
5

6. Análise de circuitos elétricos CC e CA Pedro Barros Neto
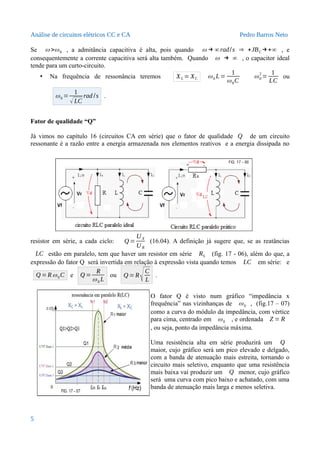
A impedância de corte também é definida em ZC =0,707Zpico e uma reta nessa ordenada vai
cruzar a curva da impedância nas abcissas f CA e f CB , correspondentes à largura da banda de
atenuação Δ f =f CA−f CB e também Δ f =
f 0
Q
, o que nos dá Q =
f 0
Δ
f .
Uma correlação entre 0,707Z e 0,5 P , na ordenada que define a banda de atenuação, pode
ser feita a partir do fato da tensão ser diretamente proporcional à impedância V =IZ , como
P=
V
2
Z
e 0,707
2
=0,5 , então 0,5 P=
0,707V
2
Z
.
A atenuação, dada em logaritmo, é a mesma calculada para o circuito RLC em série: A =−3dB .
17.6 - Exemplos
17.6.1 - CIRCUITO RC
Dados (Fig. 17- 08):
Vf P = 311,174V ω=377rd/ s R=5Ω C =100μ F
Pedem-se: IC , IR , V , Z , P , Q e FP .
Triângulo da Admitância
Considerar o módulo da tensão como referência fasorial
V ∠0° → ωt =0 rad .
Condutância: G =
1
R
G =
1
5
G =0,2S
Reatância capacitiva: XC =− j
1
ω C
XC =− j
1
377∗0,0001
XC =− j
1
0,0377
então
XC =− j26,526Ω ou na forma polar
XC =26,526Ω∠−90° .
Susceptância capacitiva: BC =
1
−j XC
BC =
[ 1
−j 26,526]
BC = j 0,0377S . Na forma polar: BC =0,0377∠90° .
Defasagem entre a tensão e a corrente: ϕ =tg−1
[j BC
G ]
ϕ =tg−1
[j0,0377
0,2 ] ϕ =10,67° .
6

7. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Funções trigonométricas de ϕ : cosϕ =0,98 e senϕ =0,185 .
Módulo da admitância: Y =√G
2
+ BC
2
Y =√(0,2)
2
+(0,0377)
2
Y =0,2035 S .
Admitância complexa na forma retangular: Y =G+ j BC ou Y = 0,2 + j 0,0377 S .
Na forma polar: Y =Y ∠ϕ ou Y = 0,2035∠10,67° S .
Triângulo das correntes
Corrente eficaz no resistor: IR = V G IR =220x 0,2
IR =44 A∠ 0° A
Corrente eficaz no capacitor: IC =V ( jBC )
IC =220( j0,03769) IC = j 8,29 A ou na forma polar
IC = Ic ∠ϕ ou IC =8,29∠10,67° .
Módulo da corrente total : I =√IR
2
+IC
2
I =√442
+8,292
I =44,77 A .
Corrente total: I = IR+ j IC I =44+ j 8,29 A na forma polar I = I ∠ϕ ou
I =44,77∠10,67° A .
Também pode ser calculada com o módulo da admitância:
I =V Y ∠ϕ I =220 x0,2035∠10,67° ou I =44,77 A∠10,67° .
Triângulo das potências:
Potência no resistor: P=IR
2
R P=442
x5 ou P=9.680 W .
Potência reativa no Capacitor:
Q =V x jIC Q =220 x j 8,29
Q = j1.824VAR na forma polar
Q =1.824 ∠90°VAR .
Módulo da potência total ou potência
aparente consumida S =√P²+Q ² S =√9.6802
+1.8242
ou S =9.850,35 VA .
Potência complexa total consumida S= P+ jQ ou S=9.680 + j1.824 . Na forma polar
S=S ∠ϕ ou S=9.850,35∠10,67° VA .
Potência total fornecida pela fonte: Sf =−(Scarga) .
Fator de potência FP=cos ϕ ou cos10,67° =0,98 .
7

8. Análise de circuitos elétricos CC e CA Pedro Barros Neto
17.6.2 - CIRCUITO RL
Dados (Fig. 17- 09):
Vf P =311,174V ω=377rd/ s R=20Ω
L=60 mH com RL=0Ω
Pedem-se: IC , IR , V , Z , P , Q e
FP .
Triângulo da Admitância
Condutância: G =
1
R
G =
1
20
ou G =0,05S .
Reatância indutiva: X L = jω L Ω XL = j 377∗0,06 XL = j 22,62Ω ou na forma polar
XL =22,62∠ 90° Ω .
Susceptância indutiva: BL =− j
[ 1
XL
]S BL =− j
[ 1
22,62 ]
ou BL =−j 0,044S .
Defasagem entre a tensão e a corrente: ϕ =(tg
−1
)[−j BL
G ]
ϕ =(tg−1
)
[−0,044
0,05 ] ϕ =(tg
−1
) [− j0,88]
ϕ =−41,347° adequar o ângulo para −j com a m.d.p. m.d . p.(−ϕ )=318,653° .
Funções trigonométricas de ϕ : cosϕ =0,75 e senϕ =−0,66 .
Módulo da Admitância: Y = √G
2
+BL
2
Y = √(0,05)2
+(−0,044)2
ou Y =0,164122 S .
Admitância complexa: Y =G− j BL Y =0,05−j 0,044 S . Na forma polar
Y =Y ∠m .d. p. (−ϕ ) ou Y =0,164122∠318,653° S .
Triângulo das correntes
Corrente no resistor:
IR =V G IR =220x 0,05 ou IR =11 ∠ 0° A .
Corrente no indutor:
8

9. Análise de circuitos elétricos CC e CA Pedro Barros Neto
IL =V (− jBL) A IL =220(− j0,044) IL =− j 9,68 A na forma polar
IL =9,68∠−90° A .
Corrente total:
Módulo I = √IR
2
+IL
2
I =√112
+9,682
ou I =14,65 A .
Corrente total: I = IR− j I L A I =11− j 9,68 A na forma polar I = I ∠m .d. p.(−ϕ ) ou
I =14,65∠318,653° A .
Triângulo das potências
Potência eficaz no resistor: P =IR
2
R P=11
2
x 20 ou P =2.420∠ 0° W .
Potência reativa no Indutor : QL =V (−j I L) QL =220(−j 13,7566) ou
Q =− j2.140,345 VAR . Na forma polar Q =2.140,345∠−90° VAR .
Módulo da potência total ou potência aparente;
S =√P²+Q ² S =√2.420²+2.140,345²
ou S =3.230,7VA .
Potência complexa total da carga:
S= P– j Q ou
S=2.420−j 2.140,345 VA . Na forma polar
S= 3230.71∠ 318,653° VA .
Potência total fornecida pela fonte: Sf = Vr I Sf =−220(11 − j 9,68)
Sf =−2.420 + 2.129,6 VA . Na forma polar Sf =−S∠ m.d. p.(−ϕ ) ou
Sf =−3.230,7∠318,653° VA .
Fator de potência: FP=cosϕ ou cos 41,49° =0,75 .
9

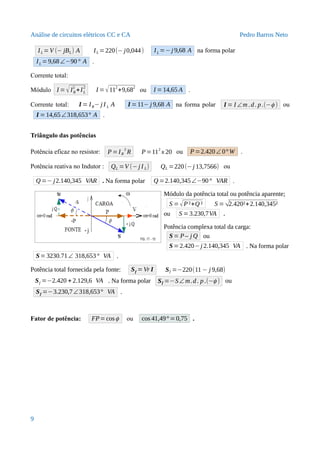
10. Análise de circuitos elétricos CC e CA Pedro Barros Neto
17.6.3 - CIRCUITO RLC (anti-ressonante)
Dados (Fig. 17 - 10):
VS =311,174 VP ω=377rd/ s R=30Ω L=120 mH com RL=0Ω e C= 50μ F
Pedem-se: IC , IL , IR , V , Z , P , Q e FP .
Considerar a tensão como referência fasorial 220∠0° V .
Triângulo da Admitância
Condutância: G =
1
R
G =
1
30
G =0,033 S .
Reatância capacitiva: XC =− j
1
ω C
XC =− j
1
377∗0,00005
XC =− j
1
0,0188495
então
XC =− j53,05Ω ou na forma polar XC = 53,05∠−90° Ω .
Susceptância capacitiva: BC =
1
− j XC
BC = j[ 1
53,05] BC = j 0,01885 S .
Reatância indutiva: XL = jω L XL = j 376,99x 0,12 XL = j 45,2388Ω ou na forma polar
XL =45,2388Ω∡90° .
Susceptância indutiva: BL =
1
j XL
BL =− j
[ 1
45,238]
BL =− j 0,022 S .
Susceptância equivalente: BEQ = BC−BL
BEQ = 0,01885− 0,022 BEQ =− j 0,00315 S com
predominância indutiva.
Ângulo de defasagem entre a tensão e a corrente:
10

11. Análise de circuitos elétricos CC e CA Pedro Barros Neto
ϕ =(tg−1
)[BEQ
G ] ϕ =(tg
−1
)
[−0,00315
0,033 ] ϕ =(tg−1
)[−0,0954] ϕ =−5,45° . Adequar
o ângulo para −j com a m.d.p. m.d . p. (−ϕ )=354,55° .
Funções trigonométricas: cosϕY =0,99 e senϕ Y =−0,095 .
Admitância
Módulo : Y =√G
2
+BEQ
2
Y =√0,0332
+ 0,003152
ou Y =0,0317 S .
Admitância total complexa: Y =G− j BEQ ou Y =0,033− j 0,0315 S . Na forma polar
Y =Y ∠m .d. p. (−ϕ ) ou Y =0,031 ∠ 354,55° S com predominância indutiva.
Triângulo das correntes
Corrente no resistor: IR =V G IR =220x 0,033... ou IR =7,33...∠0° A .
Corrente no capacitor: IC =V ( jBC ) IC =220( j0,01885) ou IC = j 4,147 A . Na forma
polar IC =4,147 ∠90° A .
Corrente no indutor: IL =V (− jBL)
IL =220(− j0,0221) ou IL =−j 4,862 A . Na forma
polar IL =4,862∠−90° .
Corrente reativa equivalente: IBEQ =IC + IL
IBEQ = j 4,147− j 4,862 ou IBEQ =− j0,715 A .
Módulo da corrente total: I =√IR
2
+IBEQ
2
I =√7,332
+0,7152
ou I = 7,368 A .
Corrente total: I = IR− j IBEQ ou I =7,33− j0,715 A . Na forma polar
I = IS ∠m.d . p. (−ϕ ) ou I =7,368∠354,55° A .
Triângulo das potências
Potência eficaz no resistor: P=IR
2
R P =7,33...2
(30) ou P=1.612 W .
Potência reativa no indutor: QL =V (−jIL) QL =220(−j 4,862) ou QL =− j1.069,64 .
Potência reativa no capacitor: QC =V ( jIC ) .
QC =220( j 4,147) QC = j 912,34 .
11

12. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Potencia reativa equivalente:
QEQ =QC + QL
QEQ =( j 912,34−j1.069,64) ou
QEQ =−j 157,3 VAR .
Potência aparente (módulo):
S = √1.6122
+ 157,322
ou
S =1.619,658 VA
Potência total fornecida pela fonte:
Sf =−V I .
Sf =−220(7,33 − j0,715) Sf =−1.612+ j157,3 VA . Na forma polar
Sf =−S∠ m.d. p.(−ϕ ) ou Sf =−1.619,658∠354,55° VA .
Fator de potência
FP=cos m.d. p. ϕ como cos354,55° =0,995 , então FP=0,995 .
Exemplo com duas impedâncias em paralelo
Dados: Fig. 17 – 20
f =
ω
2π
f =
377
6,283
ou f =60 Hz
L=
XL
ω
L=
12
377
ou L=0,031.83 H .
C =
1
ω . XC
C=
1
377x 20
ou C =0,001.326.6 F .
VP =
V
0,707
VP =
200
0,707
ou VP =282,9 V .
12

13. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Triângulo da admitância (Fig. 17 - 21)
 Z1 =2 + j12 Ω então Y1=
1
2+ j 12
ou Y1=0,0135...− j0,081... S . Na forma
polar Y1= √0,0135
2
+ 0,081
2
tg
−1
[−0,081
0,0135 ] ou Y1=0,08211…∠ – 80,54 adequar
o ângulo para −j com m.d . p.(ϕ 1)=279,46° então Y1=0,08211…∠279,46° .
 Z2 =3− j 20 Ω então Y2=
1
3− j20
ou Y2= 0,007335 + j 0,0489 S . Na forma
polar Y2=√0,007335
2
+ 0,0489
2
tg
−1
[ 0,0489
0,007335] ou Y2=0,04944…∠ 81,5° .
 YEQ =(0,00135...− j 0,081...)+(0,007335 + j 0,0489) ou
YEQ =0,020835− j 0,0321 S com predominância indutiva. Na forma polar
YEQ =√0,0208352
+ 0,03212
tg−1
[ −0,0321
0,0208355] ou YEQ =0,03826...∠−57° adequar
o ângulo para −j com m.d . p.(ϕ EQ)=303° , então YEQ =0,08211…∠303° .
Triângulo das correntes (Fig. 17 - 22)
 I1 =V (Y1) I1 =200(0,0135...−j 0,0081...) ou I1 =2,7− j16,2 A . Módulo
I1 =√2,7
2
+ 16,2
2
=16,42 A . Na forma polar I1 =I1 ∠m.d . p.(ϕ 1) ou
I1 =16,42∠279,46° A .
13

14. Análise de circuitos elétricos CC e CA Pedro Barros Neto
 I2 =V (Y2) I2 =200(0,007335 + j 0,0489) ou I2 =1,467+ j9,78 A . Módulo
I2 =√1,4672
+ 9,782
=9,89 A . Na forma polar I2 =I2 ∠ϕ 2
I2 =9,89∠81,5° A .
 IEQ =V (YEQ) IEQ =200(0,020835− j 0,0321) ou IEQ =4,167− j 6,42 A .
Módulo IEQ =√4,167
2
+ 6,42
2
=7,65377... A . Na forma polar
IEQ =I EQ ∠m.d. p.(ϕ EQ) ou IEQ =7,65377...∠303° A .
Triângulo das potências (Fig. 17 – 23)
Com a expressão (9.21) S=
V 2
Z
.
 S1 =
200
2
2 + j12
S1 =540,54− j3.243,243 VA , onde P1 =540,54 W e
Q1 =−j 3.243,243VAR . Módulo S1 =√540,54
2
+ 3.243,243
2
=3.287,98 VA .Na
forma polar S1 =S1∠ m.d. p.(ϕ 1) ou S1 =3.287,98∠279,46° VA .
 S2 =
2002
3− j20
S2 =293,4 + j1.956 VA , onde P2 =293,4 W e
Q2 = j1.956VAR . Módulo S2 =√293,4
2
+ 1.956
2
=1.977,9 VA .Na forma polar
S2 =S2 ∠m.d. p.(ϕ 2) ou S2 =1.977,9∠81,5° VA .
 SEQ = S1 + S2 SEQ =(540,54− j3.243,243)+(293,4 + j 1.956)
SEQ = 833,94− j 1.287,243 VA , onde PEQ = 833,94 W e
14

15. Análise de circuitos elétricos CC e CA Pedro Barros Neto
QEQ =−j 1.287,243VAR . Módulo SEQ =√833,942
+ 1.287,2432
=1.533,77 VA .Na
forma polar SEQ =SEQ ∠m .d. p.(ϕ EQ) ou SEQ =1.533,77∠303° VA .
Fator de potência
FP=cosϕ EQ sendo cos303° =0,54 , então FP=0,54 .
15