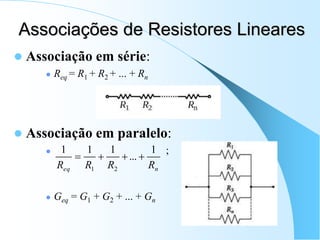
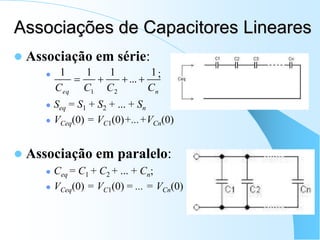
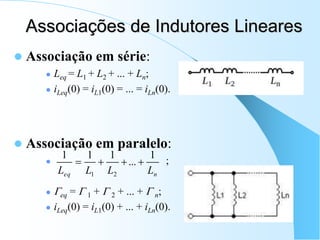
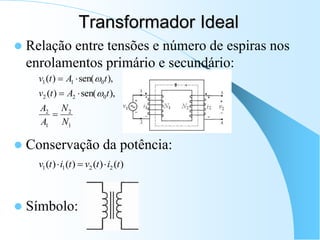
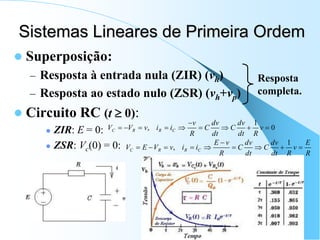
1) O documento apresenta os principais conceitos e elementos da disciplina Eletrônica I, incluindo circuitos RC e RL, transformadores, impedância e admitância. 2) São descritos os modelos de parâmetros concentrados e distribuídos para análise de circuitos, assim como as leis de Kirchhoff e os elementos passivos lineares básicos. 3) O documento fornece as definições iniciais e grandezas fundamentais da teoria de circuitos para análise de sistemas lineares de primeira ordem.

1. Eletrônica I
Prof. Ivo Carvalho
Engenharia Eletrônica

2. Bibliografia
 Desoer, C.A., Kuh, E.S., Basic Circuit Theory,
McGraw Hill, 1967.
 Sedra, A.S., Smith, K.C., Microelectronic Circuits,
3rd. ed., Harcourt Brace College Publishers, 1991.
 Nascimento, D., Slides das Aulas de Eletrônica I –
DEL-UFRJ, 2009.

3. Temas Gerais
 Introdução aos elementos discretos lineares;
 Conceitos básicos da Teoria de Circuitos;
 Dispositivos semicondutores passivos e
ativos;
 Desenho de circuitos eletrônicos simples
com amplificadores operacionais.

4. Abordagens
 Dimensões comparáveis ao menor
comprimento de onda () dos sinais de um
circuito (ex.: linhas de transmissão):
– Modelos de parâmetros distribuídos;
– Leis de Maxwell;
 Dimensões << :
– Modelos de parâmetros concentrados;
– Leis de Kirchhoff.

5. Grandezas Fundamentais
 Tensão (diferença de potencial – d.d.p.):
grandeza escalar relacionada ao campo
elétrico – unidade: volt (V);
 Corrente: escalar relacionada ao fluxo de
carga elétrica – unidade: ampère (A);
 Potência: taxa de variação da Energia –
unidade: watt (W): ;
 Energia: trabalho realizado pela corrente –
unidade: joule (J): .
)
(
)
(
)
( t
i
t
v
t
P 

dt
t
P
t
U
t


0
0
0 )
(
)
(

6. Definições Iniciais
 Nó - qualquer ponto do circuito em que dois
ou mais terminais se liguem;
 Ramo – caminho único entre dois nós
consecutivos;
 Malha ou Laço - qualquer caminho fechado
seguido sobre ramos de um circuito.

7. Leis de Kirchhoff
 Lei de Kirchhoff de Tensão (LKT ou KVL):
– A soma das tensões em uma malha, devidamente
orientadas, é nula;
 Lei de Kirchhoff de Corrente (LKC ou KCL):
– A soma das correntes que entram em um nó é nula.

8. Fontes Independentes...
 Fonte Independente de Tensão:
Pilha / Bateria Fonte DC (CC) Fonte AC
 Fonte Independente de Corrente:
Fonte DC (CC) ou AC

9. Elementos Básicos
Símbolo Geral Linear
Resistor VR = f (iR) VR = R  iR
Capacitor
Indutor



t
C
C
C dt
i
C
V
V
0
1
)
0
(
 

 dt
i
g
V C
C














dt
di
h
dt
d
h
V L
i
H
L

dt
di
L
V L
L 

10. Associações de Fontes de Tensão
 Associação em série:
 Veq = V1 + V2:
 Associação em paralelo:
 Só é válida quando V1 = V2 = Veq, caso contrário, burla a
LKT.

11. Associações de Fontes de Corrente
 Associação em série:
 Só é válida quando I1 = I2 = Ieq, caso contrário, burla a
LKC.
 Associação em paralelo:
 Ieq = I1+I2:

12. Associações de Resistores Lineares
 Associação em série:
 Req = R1 + R2 + ... + Rn
 Associação em paralelo:
 ;
 Geq = G1 + G2 + ... + Gn
n
eq R
R
R
R
1
...
1
1
1
2
1





13. Associações de Capacitores Lineares
 Associação em série:
 ;
 Seq = S1 + S2 + ... + Sn
 VCeq(0) = VC1(0)+...+VCn(0)
 Associação em paralelo:
 Ceq = C1 + C2 + ... + Cn;
 VCeq(0) = VC1(0) = ... = VCn(0)
n
eq C
C
C
C
1
...
1
1
1
2
1





14. Associações de Indutores Lineares
 Associação em série:
 Leq = L1 + L2 + ... + Ln;
 iLeq(0) = iL1(0) = ... = iLn(0).
 Associação em paralelo:
 ;
 eq =  1 +  2 + ... +  n;
 iLeq(0) = iL1(0) + ... + iLn(0).
n
eq L
L
L
L
1
...
1
1
1
2
1





15. Transformador Ideal
 Relação entre tensões e número de espiras nos
enrolamentos primário e secundário:
 Conservação da potência:
 Símbolo:
1
2
1
2
0
2
2
0
1
1
),
sen(
)
(
),
sen(
)
(
N
N
A
A
t
A
t
v
t
A
t
v







)
(
)
(
)
(
)
( 2
2
1
1 t
i
t
v
t
i
t
v 



16. Sistemas Lineares de Primeira Ordem
 Superposição:
– Resposta à entrada nula (ZIR) (vh)
– Resposta ao estado nulo (ZSR) (vh+vp)
 Circuito RC (t  0):
 ZIR: E = 0:
 ZSR: Vc(0) = 0:
0
1
, 








 v
R
dt
dv
C
dt
dv
C
R
v
i
i
v
V
V C
R
R
C
R
E
v
R
dt
dv
C
dt
dv
C
R
v
E
i
i
v
V
E
V C
R
R
C 









1
,
Resposta
completa.

17. Sistemas Lineares de Primeira Ordem
 Respostas:
– ZIR: ;
– ZSR: ;
– Completa: .
 ZIR + ZSR vs.
Transiente + Regime Permanente:
– Transiente (ou transitório): decai com o tempo;
– Regime permanente: mantém-se com
comportamento intimamente associado à entrada:
 .
0
,
)
(
1
0 


t
e
V
t
v
t
RC
0
),
1
(
)
(
1





t
e
E
t
v
t
RC
0
),
1
(
)
(
1
1
0 






t
e
E
e
V
t
v
t
RC
t
RC
0
,
)
(
)
(
1
0 




t
E
e
E
V
t
v
t
RC

18. Sistemas Lineares de Primeira Ordem
 Circuito RL (t  0):
 ZIR: I = 0:
 ZSR: IL(0) = 0:
 Respostas:
– ZIR: ;
– ZSR: ;
– Completa: .
 Transiente + Regime Permanente:
0
, 










 i
R
dt
di
L
dt
di
L
R
i
v
v
i
i
i L
R
R
L
I
R
i
R
dt
di
L
dt
di
L
R
i
I
v
v
i
i
I
i L
R
R
L 










 )
(
,
0
,
)
( 0 


t
e
I
t
i
t
L
R
0
),
1
(
)
( 




t
e
I
t
i
t
L
R
0
),
1
(
)
( 0 






t
e
I
e
I
t
i
t
L
R
t
L
R
0
,
)
(
)
( 0 




t
I
e
I
I
t
i
t
L
R

19. Sistemas Lineares de Primeira Ordem
 Entrada senoidal (ZSR):
– Entrada: ;
– Homogênea: ;
– Particular: ;
– Completa: .

0
,
)
(
1
0 


t
e
V
t
v
t
RC
h
0
),
cos(
)
( 2 

 t
t
A
t
vp 

0
),
cos(
)
( 1 
 t
t
A
t
E 
0
),
cos(
cos
)
(
)
(
)
( 2
1
2 








t
t
A
e
A
t
v
t
v
t
v
t
RC
p
h 


2
1
2
1
1
2
)
( C
C
R
A
A











 

RC

 
1
tan 1
2

20. Impedância Elétrica
 Fontes senoidais...
– Elementos simples operando em regime
permanente:
Resistor Capacitor Indutor
 ;
 ;
 ;
 .
)
cos(
)
( 0t
t
i 

)
cos(
)
( 0t
R
t
vR 


)
cos(
)
sen(
)
cos(
)
( 2
0
1
0
1
0
1
0
0





 


  t
t
dt
t
t
v C
C
C
C
)
cos(
)
sen(
)
( 2
0
0
0
0
)
cos( 0 




 





 t
L
t
L
L
t
v dt
t
d
L

21. Fasores e Números Complexos
 Senóides como exponenciais complexas:
Resistor Capacitor Indutor
 ;
 ;
 ;
 .
 
)
(
Re
)
cos(
)
(
)
( 0
0
t
i
t
t
i
e
t
i C
t
j
C 


 

)
(
)
cos(
)
( 0 t
i
R
t
R
t
vR 


 





 









 )
(
Re
)
(
Re
)
cos(
)
(
0
0
2
0
1
0
t
i
C
j
C
j
t
i
t
t
v C
C
C
C


 

 
)
(
Re
)
cos(
)
( 0
2
0
0 t
i
L
j
t
L
t
v C
L 



 

 

22. Impedância e Admitância
 Impedância = Resistência + Reatância:
 Resistores: resistência R (real);
 Indutores: reatância indutiva XL() = L – imaginária positiva;
 Capacitores: reatância capacitiva XC() = 1/(C) – imaginária negativa.
 Associação em série: Z() = R + j (XL - XC) (soma fasorial).
 Admitância = Condutância + Susceptância (“permitância”):
 Resistores: condutância G (real);
 Indutores: susceptância indutiva BL() = 1/(L) – imaginária negativa;
 Capacitores: susceptância capacitiva BC() = C – imaginária positiva.
 Assoc. em paralelo: Y() = G + j (BC - BL) (soma fasorial).

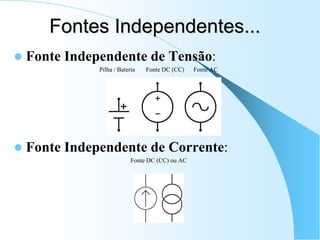
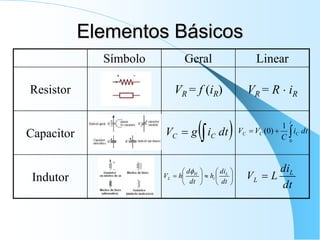
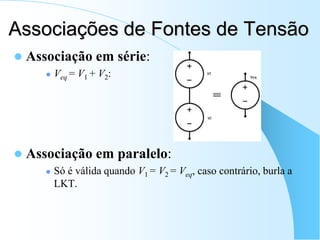
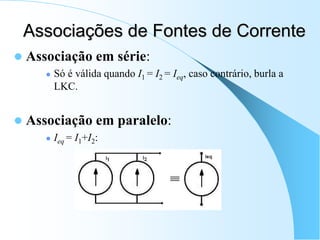
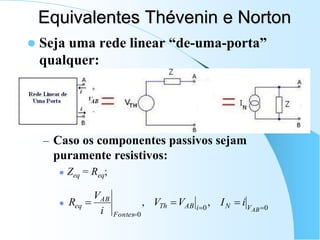
23. Voltando ao Circuito RC...
– Entrada [E(t)]: ;
– Saída [VC(t)]: ;
 Em regime permanente:
– Função de Transferência (é função de ):
0
),
cos(
)
( 1 
 t
t
A
t
E 
0
),
cos(
cos
)
(
)
(
)
( 2
1
2 








t
t
A
e
A
t
v
t
v
t
v
t
RC
p
h 


)
cos(
)
( 2 
 
 t
A
t
v
   
































RC
Z
jX
H
Z
X
A
A
R
H
R
H
C
C
C
C
C
j
C
j









1
tan
)
(
)
(
,
)
(
)
(
)
(
1
2
1
2
2
1
2
1
2
1
2
1
1
2
)
( C
C
R
A
A











 

RC

 
1
tan 1
2

24. Equivalentes Thévenin e Norton
 Seja uma rede linear “de-uma-porta”
qualquer:
– Caso os componentes passivos sejam
puramente resistivos:
 Zeq = Req;

0
0
0
,
, 





AB
V
N
i
AB
Th
Fontes
AB
eq i
I
V
V
i
V
R

25. E se houver um elemento não-linear?
 Abordagens:
– Isolar o elemento não-linear e reduzir toda a parte
linear a um Equivalente Thévenin ou Norton:
Ex.:
– Utilizar uma aproximação linear do elemento não-
linear:
 modelos simplificados de uso geral;
 modelos para pequenos sinais...

26. O Diodo Semicondutor
 Junção P-N:
– Operação:
 Equação geral:
onde:
• IS – corrente de saturação ou de escala,
da ordem de 10-15 ~ 10-9 A (dobra apro-
ximadamente a cada aumento de 5°C);
• VT – tensão térmica  26 mV a 25°C (kT/q);
• n  2 para diodos discretos e  1 para
diodos integrados.
• Para cada década de aumento de corrente,
aumento de cerca de 60 mV (n=1) ou
120 mV (n=2) na tensão direta;
• VD entre cerca de 0,6 e 0,8 V na gama de operação de um diodo.
)
1
( 
  T
D
V
n
V
S
D e
I
I

27. Diodo – Modelos Lineares
Modelo de
Pequenos Sinais:
D
T
I
V
n
rd



28. Tipos de Diodo
 Polarizações de operação:
– Direta / reversa:
 Genérico (Vd  0,7V);
 Schottky (metal-semicondutor; Vd  0,3V);
 Túnel (GHz, efeitos quânticos);
– Direta:
 Schokley (PNPN - pulsos);
 LED (Vd depende da cor);
– Reversa:
 Fotodiodo;
 Varicap;
– Ruptura:
 Zener.

29. Aplicações de Diodos
 Retificador de Meia-Onda:
–
– Tensão inversa de pico:
 VIp = VSp











0
0
0
),
(
,
0
D
S
D
S
d
out
D
S
out
V
V
V
V
r
R
R
V
V
V
V

30. Aplicações de Diodos
 Retificador de Onda Completa:
– Transformador com tomada central
–
– Tensão inversa de pico:
 VIp = 2VSp – VD0











0
0
0
),
(
,
0
D
S
D
S
d
out
D
S
out
V
V
V
V
r
R
R
V
V
V
V

31. Aplicações de Diodos
 Retificador de Onda Completa:
– Ponte de diodos
–
– Tensão inversa de pico:
 VIp = VSp – 2VD0 + VD0
= VSp – VD0














0
0
0
2
),
2
(
2
,
0
D
S
D
S
d
out
D
S
out
V
V
V
V
r
R
R
V
V
V
V

32. Aplicações de Diodos
 Retificador + Filtro Capacitivo:
– Capacitor C em paralelo com a carga R
– Meia Onda Onda Completa:
 
 
r
p
L
DP
r
p
L
DM
p
r
V
V
I
i
V
V
I
i
R
C
f
V
V
/
2
2
1
/
2
1










  
 
)
2
/(
2
1
)
2
/(
1
2
r
p
L
DP
r
p
L
DM
p
r
V
V
I
i
V
V
I
i
R
C
f
V
V













33. Aplicações de Diodos
 Regulador Zener:
– Análise geral (via Thévenin):
– Regulação de linha:
– Regulação de carga:
L
Z
R
R
S
Z
Z
Z
Z
L
i
i
i
R
i
V
r
i
V
V
V








 0
)
//
(
0 R
r
i
r
R
r
V
r
R
R
V
V Z
L
Z
Z
S
Z
Z
L 




Z
Z
S
L
r
R
r
V
V




)
//
( R
r
I
V
Z
L
L





34. Aplicações de Diodos
 Circuitos Limitadores ou Ceifadores (Clipping):

35. Aplicações de Diodos
 Circuitos Grampeadores (Clamping):
– Grampeador positivo:
– Grampeador negativo:

36. Aplicações de Diodos
 Dobradores de Tensão:
– Meia onda ou “em cascata”:
– Onda completa:

37. Aplicações de Diodos
 Multiplicador de Tensão:

38. Redes de Duas Portas
 Genéricas vs. Lineares:
– Parâmetros-y:
– Parâmetros-z:
– Parâmetros-h:
– Parâmetros- g:







2
22
1
21
2
2
12
1
11
1
V
y
V
y
I
V
y
V
y
I







2
22
1
21
2
2
12
1
11
1
I
z
I
z
V
I
z
I
z
V







2
22
1
21
2
2
12
1
11
1
V
h
I
h
I
V
h
I
h
V







2
22
1
21
2
2
12
1
11
1
I
g
V
g
V
I
g
V
g
I
0
1
1
11
2

I
V
I
g
0
2
1
12
1

V
I
I
g
0
1
2
21
2

I
V
V
g
0
2
2
22
1

V
I
V
g

39. Amplificadores
 Redes de duas portas (idealmente, unidirecionais) que
visam aumentar a magnitude de um sinal
preservando sua morfologia...
 Simbologia:
– Ganhos:
 de Tensão: , de Corrente: , de Potência:
– Amplificador de Tensão ideal:
 g11=0, g12=0, g22=0, g21=Av.
i
o
v
V
V
A 
i
o
i
I
I
A  i
v
i
i
o
o
p A
A
I
V
I
V
A 


40. Amplificadores
 Representação do Ganho em decibéis (dB):
– Ganho de tensão = 20log10(|Av|) dB;
– Ganho de corrente = 20log10(|Ai|) dB;
– Ganho de potência = 10log10(Ap) dB.
– Não confundir valores negativos em Ax e em dB!
 Se o ganho de potência é maior que 1 (> 0 dB):
– Potência entregue à carga > potência recebida da fonte...
– Necessidade de fonte externa:
 Pdc = V1 I1 + V2 I2;
 Pdc + PI = PL + Pdiss;
 Eficiência:
%
100


dc
L
P
P


41. Amplificadores
 Saturação:
– Operação:
v
i
v A
L
v
A
L 




42. Amplificadores
 Não-Linearidade e Polarização (Biasing):
– Operação:
 Vi(t) = vi(t) + vi0;
 Vo(t) = vo(t) + vo0;
 vo(t)  Av· vi(t) :
Q
i
o
v
dv
dv
A 

43. Modelos para Amplificadores
Tipo Modelo Parâmetro de Ganho Características
Ideais
Amplificador de
Tensão
Ganho de tensão de
circuito aberto
Ri = 
Ro = 0
Amplificador de
Corrente
Ganho de corrente de
curto-circuito
Ri = 0
Ro = 
Amplificador de
Transcondutância
Transcondutância de
curto-circuito
Ri = 
Ro = 
Amplificador de
Transresistência
Transresistência de
circuito aberto
Ri = 0
Ro = 0
)
V/V
(
0


o
i
i
o
vo
v
v
A
)
A/A
(
0


o
v
i
o
is
i
i
A
)
A/V
(
0


o
v
i
o
m
v
i
G
)
V/A
(
0


o
i
i
o
m
i
v
R

44. Amplificadores
 Exemplos:
– Cascateamento de três estágios de amp. de tensão:
– Transistor bipolar (modelo simplificado de pequenos sinais):

45. Amplificadores
 Resposta em freqüência:
– Ilustração com base no Amp. de Tensão:
– Largura de banda (bandwidth - BW):
 pontos de 3dB...
)
sen(
)
( t
V
t
v i
i 
 )
sen(
)
( 
 
 t
V
t
v o
o
)
(
)
(
)
(
)
(








T
V
V
T
i
o

46. Amplificadores
 Resposta em freqüência:
– Exemplo – acoplamento DC (filtro passa-altas):
io = Gm.vi

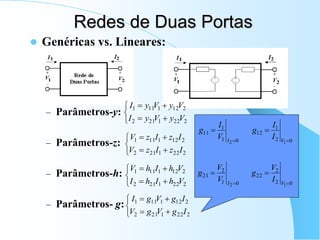
47.  Modelo Real Simplificado vs. Modelo Ideal:
Real Simplificado: Ideal:
 A muito grande;  A  
 Ri muito grande;  Ri  ;
 BW: [0 , fH], fH muito grande.  BW  [0 , ).
Realimentação Negativa!!
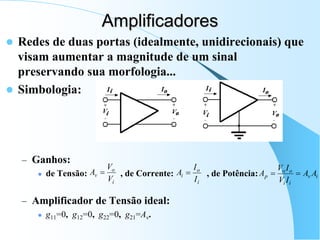
Amplificadores Operacionais
)
( 
 



 v
v
A
v
A
v i
o
vi  0, para vo finito
em operação linear

48.  Exemplo – Determine o ganho A para:
– Gm = 10 mA/V;
– R = 10 k;
–  = 100.
Amplificadores Operacionais

49.  Estrutura interna do famoso Amp. Op. 741:
Amplificadores Operacionais

50.  Configurações básicas (considerando o modelo ideal):
Amplificador Não-Inversor Amplificador Inversor
 
 ; 
 Ro = 0;  Ro = 0.
 Para R1  : seguidor unitário (buffer unitário).
Amplificadores Operacionais
1
2
1
R
R
R
v
v
A
i
o 





i
i
in
i
v
R
1
2
R
R
A 

1
R
i
v
R
i
i
in 

Dificuldade prática para
fazer A e Rin elevados...

51.  Exemplo - Amplificador Inversor alternativo:
– Requisitos de projeto:
 A = 100;
 Rin = 1 M;
 R’s  1 M.
Amplificadores Operacionais













3
4
2
4
1
2
1
R
R
R
R
R
R
v
v
A
i
o

52.  Somador Inversor:
Amplificadores Operacionais












 n
n
f
f
f
o v
R
R
v
R
R
v
R
R
v 
2
2
1
1

53.  Amplificador Diferencial:
– Pontos fracos:
 Baixa impedância de entrada;
 Dificuldade para alterar o ganho.
Amplificadores Operacionais
 
1
_
1
2
1
2
2 R
R
v
v
R
R
v
Diff
in
o





54.  Algumas aplicações com capacitor e resistor:
Integrador Diferenciador
Amplificadores Operacionais




t
i
c
o dt
t
v
R
C
v
t
v
0
0 )
(
1
)
(
dt
t
dv
R
C
t
v i
o
)
(
)
( 

