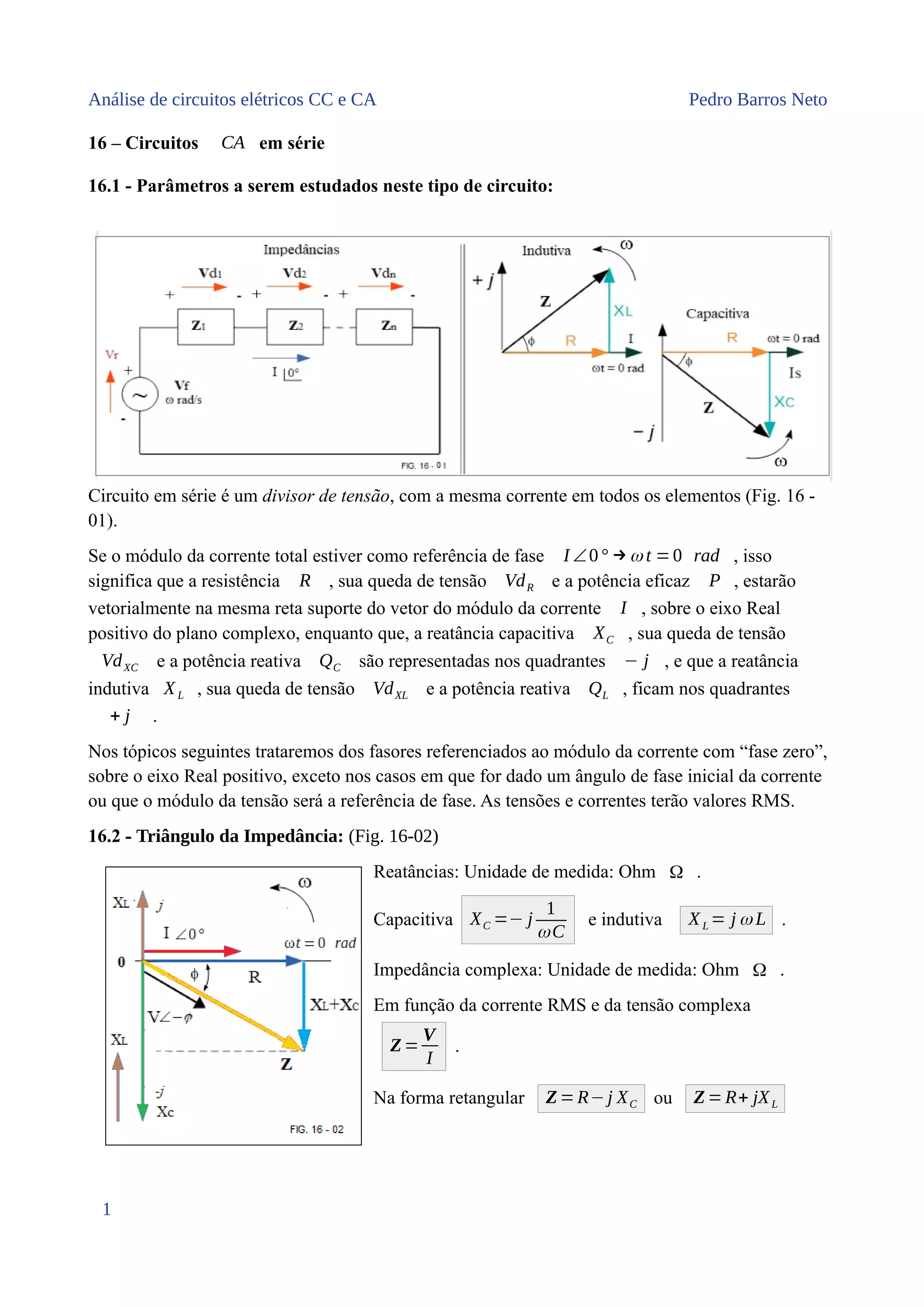
O documento descreve os principais parâmetros a serem estudados em circuitos elétricos CA em série, incluindo triângulos de impedância, tensão e potência. Circuitos em série são divisores de tensão com a mesma corrente em todos os elementos. A impedância total é dada pela soma das impedâncias dos elementos.

1. Análise de circuitos elétricos CC e CA Pedro Barros Neto
16 – Circuitos CA em série
16.1 - Parâmetros a serem estudados neste tipo de circuito:
Circuito em série é um divisor de tensão, com a mesma corrente em todos os elementos (Fig. 16 -
01).
Se o módulo da corrente total estiver como referência de fase I ∠0° →ω t =0 rad , isso
significa que a resistência R , sua queda de tensão VdR e a potência eficaz P , estarão
vetorialmente na mesma reta suporte do vetor do módulo da corrente I , sobre o eixo Real
positivo do plano complexo, enquanto que, a reatância capacitiva XC , sua queda de tensão
VdXC e a potência reativa QC são representadas nos quadrantes − j , e que a reatância
indutiva XL , sua queda de tensão VdXL e a potência reativa QL , ficam nos quadrantes
+ j .
Nos tópicos seguintes trataremos dos fasores referenciados ao módulo da corrente com “fase zero”,
sobre o eixo Real positivo, exceto nos casos em que for dado um ângulo de fase inicial da corrente
ou que o módulo da tensão será a referência de fase. As tensões e correntes terão valores RMS.
16.2 - Triângulo da Impedância: (Fig. 16-02)
Reatâncias: Unidade de medida: Ohm Ω .
Capacitiva XC =− j
1
ωC
e indutiva XL = j ω L .
Impedância complexa: Unidade de medida: Ohm Ω .
Em função da corrente RMS e da tensão complexa
Z=
V
I
.
Na forma retangular Z=R−j XC ou Z=R+ jXL
1

2. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Na forma polar: Módulo da impedância Z = √R
2
+ XEQ
2
ou Z =
V
I
.
Predominância indutiva: Z=Z ∠ ϕ .
Predominância capacitiva: Z=Z ∠m.d. p.(−ϕ ) .
Com o módulo da impedância poderemos ter: Z=Zcosϕ ± j(Z senϕ ) onde R=Z cosϕ é a
parte real e XL = j(Z senϕ ) ou XC =− j(Z senϕ ) a parte Imaginária.
Nota: quando lidarmos com elementos reativos práticos, deveremos considerar que eles têm
resistências internas e capacitâncias ou indutâncias parasitas.
Ângulo da defasagem entre a corrente e a tensão:
• Circuito RL ϕ =(tg
−1
)
XL
R
.
• Circuito RC ϕ =(tg
−1
)[−j XC
R ] .
• Circuito RLC ϕ =(tg
−1
)[±j XEQ
R ] .
Como consequência, teremos: cosϕ =
R
Z
senϕ L =
jXL
Z
senϕ C =
−jXC
Z
.
Para ângulo negativo (predominância capacitiva), converter para a “menor determinação positiva”:
m.d . p. (−ϕ )=−ϕ + 360° .
16.3 - Triângulo das Tensões: (Fig. 16-03)
Tendo o módulo da corrente eficaz como referência fasorial IRMS ∠0° , a tensão complexa será
dada por V = I . ZEQ .
A queda de tensão total de um circuito em série é a soma das quedas de tensão de cada elemento.
LTK Vf =Vd1 + Vd2 + ...+Vdn .
Queda de tensão sobre resistor: VdR =I R ,
Queda de tensão sobre capacitor: VdC = I .(− jXC ) .
Queda de tensão instantânea em função da Capacitância e da integral da corrente instantânea
(relação constitutiva): v(t )=
1
C
∫
0
t
i(t )dt .
2

3. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Queda de tensão sobre indutor: VdL = I .( jXL) .
Queda de tensão instantânea em função da Indutância e da derivada da corrente instantânea (relação
constitutiva): v(t )= L
di(t )
dt
.
Num circuito com impedâncias, o módulo da queda de tensão da malha é dado por:
Vd EQ =√VdR
2
+Vd XEQ
2
.
Queda de tensão total:
• Com o módulo da corrente com valor RMS e a impedância V dEQ =I . Z .
Elevação de tensão da fonte: os fasores serão simétricos aos fasores da carga.
• Com o módulo da corrente com valor RMS e a impedância Vf =−[I .Z] .
16.4 - Triângulo das potências: (Fig. 16-04)
A potência total complexa S é medida em VA ou
Volt− Ampere (assunto já tratado no capítulo 9).
Potência total na forma retangular S= PR ±jQEQ , com:
PR = I ²R ou PR =
V2
R
.
e Q =I2
(± j XEQ) ou Q =
V2
± j XEQ
.
Módulo da potência total ou potência aparente
S =√P2
+(±j QEQ)2
.
3

4. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Potência total na forma polar S=S ∠ϕ para carga indutiva e S=S ∠m.d . p.(−ϕ ) para
carga capacitiva.
Potência total na carga:
• Com fasores cujos módulos são valores de pico S=
1
2
V .I
∗
onde I
∗
é o fasor do
conjugado da corrente.
• Com fasores cujos módulos são valores RMS S=V . I∗
• Com o módulo da tensão RMS com fase zero e o fasor da corrente: S=V .I∗
.
• Com o módulo da corrente RMS com fase zero e o fasor da tensão: S=V .I .
• Com o módulo da corrente RMS e a impedância S= I2
.Z .
• Com o módulo da tensão RMS e a impedância S=
V 2
Z
.
Potência total fornecida pela fonte: os fasores serão simétricos aos fasores da carga.
• Com o módulo da tensão RMS e a impedância Sf =−[V2
Z ] .
• Com o módulo da corrente RMS e a impedância Sf =−[I
2
Z] .
Fator de potência: FP=cosϕ , FP=
R
Z
e FP=
P
S
.
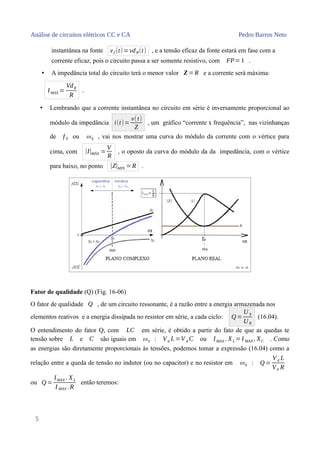
16.5 - Ressonância de um circuito RLC em série (Fig. 16 - 05)
No capítulo 8 já vimos que a reatância capacitiva decai de forma exponencial com o aumento da
frequência, enquanto que a reatância indutiva cresce de forma linear, com isso, quando ω < ω0
predomina a reatância capacitiva e quando ω > ω0 predomina a reatância indutiva.
Na frequência de ressonância ou “frequência natural” teremos |XL|−|XC|=0Ω e isso implica
em:
• ω0 L=
1
ω0C
ω0
2
=
1
LC
ou ω0 =
1
√LC
rad /s .
• A energia reativa é trocada entre o capacitor e o indutor.
• As quedas de tensão sobre de L e C serão iguais, mas com fases opostas, portanto,
cancelam-se, fazendo com que estes componentes comportem-se como curto circuito. Neste
caso, pela LTK, a queda de tensão instantânea no resistor será igual à elevação de tensão
4

5. Análise de circuitos elétricos CC e CA Pedro Barros Neto
instantânea na fonte vf (t)=vdR(t) , e a tensão eficaz da fonte estará em fase com a
corrente eficaz, pois o circuito passa a ser somente resistivo, com FP=1 .
• A impedância total do circuito terá o menor valor Z =R e a corrente será máxima:
IMAX =
VdR
R
.
• Lembrando que a corrente instantânea no circuito em série é inversamente proporcional ao
módulo da impedância i(t)=
v(t)
Z
, um gráfico “corrente x frequência”, nas vizinhanças
de f 0 ou ω0 , vai nos mostrar uma curva do módulo da corrente com o vértice para
cima, com |I|MÁX =
V
R
, o oposto da curva do módulo da da impedância, com o vértice
para baixo, no ponto |Z|MIN =R .
Fator de qualidade (Q) (Fig. 16-06)
O fator de qualidade Q , de um circuito ressonante, é a razão entre a energia armazenada nos
elementos reativos e a energia dissipada no resistor em série, a cada ciclo: Q =
U X
U R
(16.04).
O entendimento do fator Q, com LC em série, é obtido a partir do fato de que as quedas te
tensão sobre L e C são iguais em ω0 : Vd L=V d C ou IMAX . XL =I MAX . XC . Como
as energias são diretamente proporcionais às tensões, podemos tomar a expressão (16.04) como a
relação entre a queda de tensão no indutor (ou no capacitor) e no resistor em ω0 : Q =
V d L
Vd R
ou Q =
IMAX . XL
I MAX .R
então teremos:
5

6. Análise de circuitos elétricos CC e CA Pedro Barros Neto
• Q =
XL
R
ou Q =
ω0 L
R
.
• Q =
1
XC R
ou Q =
1
Rω0 C
.
• Q=
1
R √L
C
Estas expressões mostram que o fator Q é inversamente proporcional ao valor de R : quanto
maior for R , menor será o fator de qualidade Q .
Hipoteticamente, se R→0 , teríamos um caso em que a corrente (e a potência dissipada)
tenderiam para o infinito, o que não ocorre na prática, haja vista as resistências residuais nos
indutores e condutores.
Graficamente o fator de qualidade é visualizado pela largura da “base” do vértice do gráfico da
“corrente x frequência” , tomada no ponto de ordenada 0,707 I MAX .
Uma linha horizontal passando por esta ordenada vai cruzar a curva da corrente em dois pontos,
simétricos em relação à abcissa f 0 , e cujas abcissas, f CB frequência de corte baixa e f CA
frequência de corte alta, determinarão a largura da banda de frequências: Δ f =f CA −f CB ou
Δ f =
f 0
Q
e também Δ f =
R
2π L
. Nesta última expressão podemos ver que Δ f será maior
quanto maior for R , e menor será o fator de qualidade Q. Como Δ f =
f 0
Q
, então Q =
f 0
Δ f
.
As frequências de corte são definidas pela condição XL−XC =R ou R−XL+
1
XC
=0 e suas
expressões serão deduzidas no capítulo de filtros passivos.
O gráfico “potência x frequência” também mostra o fator de qualidade da sintonia. Neste caso,
haverá uma correspondência entre a corrente e a potência, nas frequências de corte, definida por:
6

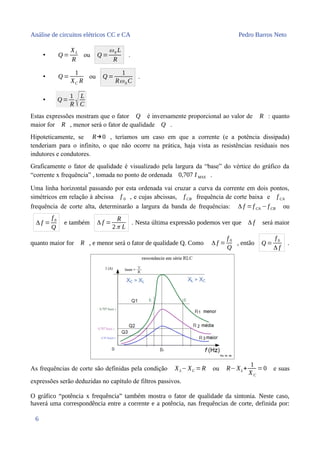
7. Análise de circuitos elétricos CC e CA Pedro Barros Neto
P(f corte)= 0,707 IMAX
2
R e sendo 0,707=
1
√2
, teremos: P(f corte)=
[IMAX
√2 ]
2
R ou
P(f corte)=
I MAX
2
2
R ou P(f corte)=
1
2
PMAX .
Se quisermos indicar o nível de atenuação nas duas frequências de corte, correspondentes a “meia
potência”, basta aplicarmos:
P(f corte)=
PMAX
2
ou P
(f corte)
PMAX
=0,5 . Aplicando a fórmula: A(dB)=10log P
(f corte )
PMAX
ou
A(dB)=10log 0,5 . Como na tabela ou na calculadora, log 0,5=−0,3 , teremos
A(dB)=10∗(−0,3) ou A =−3dB .
Nos dois pontos das curvas de corrente ou potência, que correspondem às frequências de corte,
temos as seguintes características:
• I =
I MAX
√2
, Z=√2 R , P=
PMAX
2
e ϕ =±45° ou ±π
2
rd onde tgϕ =±1
16.6 - Exemplos
16.7.1 – CIRCUITO RC
Exemplo de circuito RC em série:
Dados (Fig. 16 - 07):
Vf =311,174V P ω=377rd/ s R= 10Ω
C=100μ F
Pedem-se: VC , VR , I , Z , P , Q e FP .
Resolvendo:
Converter a tensão da fonte, de valor de pico para valor RMS:
Vf =0,707V P Vf =(0,707)311,174 Vf =220V .
Converter a frequência angular da fonte de rd /s em Hz: ω=2πf ou f =
ω
2π
f =
377
6,28318
ou f =60 Hz .
Reatância capacitiva: XC =− j
1
ω C
XC =− j
1
377∗0,0001
XC =− j
1
0,0377
então
XC =− j26,526Ω ou na forma polar XC = 26,526Ω∡−90° .
7

8. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Triângulo da impedância (Fig. 16-08):
Impedância complexa na forma retangular: Z=R−j XC ou Z =10Ω−j 26,526Ω .
Impedância complexa na foma polar, com predominância capacitiva: Z= Z ∠m.d. p(−ϕ ) .
Módulo Z =√R
2
+ XC
2
Z =√102
+(−26,526)2
ou Z =28,348Ω .
Ângulo de defasagem entre a corrente e a tensão:
ϕ =(tg
−1
)[XC
R ] ϕ =(tg
−1
)
[−26,526
10 ] ϕ =−69,3° adequar o
ângulo para −j com a m.d.p. ϕ =290,65° .
Então, teremos: Z=28,348Ω∠ 290,65° .
Módulo da corrente I =
V
Z
I =
220
28,348
ou I = 7,76 ∠0° A .
Triângulo das Tensões (Fig. 16-08):
Queda de tensão sobre o resistor:
VdR =IR VdR =7,76x 10 ou VdR =77,6∠0° V .
Queda de tensão sobre o capacitor:
VdC = I (−jXC) VdC =7,76 x26,526∠−90° ou
VdC =205,85V ∠−90° .
Queda de tensão equivalente na carga:
Na forma retangular VdEQ =VdR − jVdC V ou
V dEQ =77,6− j205,85V . Na forma polar o módulo será
V dEQ = √77,66
2
+ 205,85
2
ou V dEQ =220 V , e então
V dEQ =220∠290,65° V .
Elevação de tensão na fonte:
Com o módulo da corrente e a impedância V r =−[I .Z]
V r =−[7,76(10− j 26,526)] V r =−77,6 + j 205,8417 .
Na forma polar Vr =−[√77,6
2
+ 205,8417
2
] ou V r =−220∠ 290,5° V .
Triângulo das Potências (Fig. 16-10):
Potência no resistor: PR = I
2
R PR =7,76
2
x10 PR =602,3W
8

9. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Potência reativa no Capacitor: Q =− jVdC x I Q =(− j 205,85)7,76 Q =− j1.597,4VAR
na forma polar Q =1.597,4 ∠−90° VAR .
Módulo da potência total ou potência aparente S =√P²+Q ² S =√602,272
+1.597,642
ou
S =1.707,39 VA .
Potência total na carga na forma retangular S= P − jQ ou S=602,3− j 1.597,4 VA . Na
forma polar S=S ∠ϕ ou S=1.707,39∠−69,5° adequando o ângulo para −j com a
m.d.p. S=1.707,39∠290,5° .
Potência total entregue pela fonte: Sf =−(I
2
Z)
Sf =−[7,76
2
(10− j 28,348)] , na forma retangular
Sf =−602,27 + j 1.597,64 . Na forma polar Sf =−Sf ∠ϕ ou
Sf =−1.707,39∠290,5° .
Fator de potência
FP=cosϕ cos290,65° =0,3547 .
O FP ideal ocorre quando a carga é puramente resistiva, ou seja,
a impedância será igual à resistência, o ângulo ϕ =0rd , e
consequentemente cosϕ =1 . A potência ativa P será igual à
potência aparente S , e a potência reativa Q será nula.
Neste exemplo o FP é baixo, pois apenas 35 % da energia é
gasta sobre o resistor, enquanto 65% é trocada entre a fonte e o
capacitor.
16.6.2 - CIRCUITO RL (Fig. 16-11):
Dados:
Vf =311,174V P ω=377rd/ s R= 10Ω
L=100mH RL =0Ω (indutor ideal).
Pedem-se: VLC , VR , I , Z , P , Q e FP .
Reatância indutiva: XL = jω L XL = j 377 x0,1 então
XL = j 37,7Ω ou na forma polar XL =37,7Ω∠90° .
9

10. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Triângulo da impedância (Fig. 16-12):
Impedância complexa na foma retangular: Z=R+ j XL ou Z =10Ω+ j37,7Ω
Impedância complexa na foma polar, com predominância indutiva: Z=Z ∠ϕ .
Módulo Z = √R
2
+ XL
2
Z =√10
2
+37,7
2
ou Z =39Ω .
Ângulo de defasagem entre a corrente e a tensão:
ϕ =(tg
−1
)[XL
R ] ϕ =(tg
−1
)
[37,7
10 ] ou ϕ =75,14° .
Módulo da corrente: com os módulos da tensão e da impedância
I =
V
Z
I =
220
39
ou I = 5,64 ∠0° A .
Triângulo das Tensões (Fig. 16-13):
Queda de tensão eficaz sobre o resistor:
VdR =IR VdR =5,64 x10 ou VdR =56,41V ∠0° .
Queda de tensão sobre o indutor:
VdL = I ( jXL) VdL =5,64 x( j 37,7) VdL =212,63∠90°V .
Queda de tensão equivalente na carga:
VdEQ =VdR + jVdL V dEQ =56,41 + j212,63 V . Na forma polar
o módulo será VdEQ =√56,41
2
+ 212,63
2
VdEQ =220 V ou
V dEQ =220∠75,14° V .
Elevação de tensão na fonte:
Com o módulo da corrente e a impedância V r =−[I .Z] V r =−[5,64(10 + j 37,7)]
V r =−56,4 − j212,628 . Na forma polar V r =−V f ∠75,14° ou
V r =−220∠ 75,14° V .
10

11. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Triângulo das potências (Fig. 16-14):
Potência no resistor: PR = I
2
R P=5,64
2
x 10 ou PR =318W .
Potência reativa no Indutor: Q =VdL x I Q = j212,63 x5,64 ou Q = j1.200VAR na forma
polar Q =1.200∠ 90° VAR .
Módulo da potência total, ou potência aparente S =√P
2
+ Q
2
S =√3182
+1.2002
S =1.241,42VA .
Potência total na forma retangular S=318+ j1.200 VA . Na
forma polar S=S ∠ϕ ou S=1.241,42∠75,14° VA .
Potência total entregue pela fonte: S=−[ I
2
Z] .
Sf =−[(5,642
)10+ j37,7] ou, na notação retangular:
Sf =−318− j 1.200 VA , onde P =−318,13W e
Q =− j1.200VAR . Na notação polar S=−S ∠ϕ , então
Sf =−1.240,8∠75,14° VA .
Fator de potência
FP =cos ϕ cos75,141°=0,25639 .
Neste exemplo o FP também é baixíssimo, pois apenas 25,639 %
da energia é gasta sobre o resistor, enquanto 74,361% é trocada entre
a fonte e o indutor.
16.6.3 - CIRCUITO RLC EM SÉRIE
(ressonante de tensão) (Fig. 16-15):
Dados:
Vf =311,174V P ω=376,99rd/s
R=50Ω L=6 0mH @RL = 0Ω (indutor
ideal) C=60μ F . Adotar a corrente como
referência de fase.
Pedem-se: VLC , VR , VC , I , Z ,
P , Q e FP .
Reatâncias
Indutiva: XL = jω L XL = j 377 x0,06 então XL = j 22,62Ω ou na forma polar
XL =22,62∠ 90°Ω .
11

12. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Capacitiva: XC =− j
1
ω C
XC =− j
1
377 x0,00006
XC =− j
1
0,0226
então
XC =− j 44,2Ω ou na forma polar XC =44,2∠−90°Ω .
Reatância equivalente: XEQ = XL−XC XEQ =22,6194−44,2 então XEQ =− j21,6Ω ou na
forma polar XEQ =21,6 ∠−90° Ω com predominância capacitiva.
Ângulo de defasagem entre a corrente e a tensão:
ϕ =(tg
−1
)[−jXC
R ] ϕ =(tg
−1
)
[−21,6
50 ] ϕ =−23,36° adequar o ângulo para −j com a
m.d.p. ϕ =336,63° .
Na notação polar Z=Z ∠m.d. p.(−ϕ ) Z=54,46Ω∠ 336,63° Ω .
Triângulo da impedância (Fig. 16-16):
Com o valor da resistência e do módulo da reatância equivalente já
podemos calcular o módulo da impedância: Z =√R
2
+ XEQ
2
Z =√502
+21,592
ou Z =54,46 Ω .
Impedância complexa: na forma retangular Z=R− jXEQ ou
Z=50− j21,6Ω . na forma polar Z=Z ∠ϕ ou
Z=54,46∠336,63° Ω .
Módulo da corrente:
Como a corrente está como referência de fase (zero), basta calcular o
seu módulo pela Lei de Ohm, com os módulos da tensão eficaz e da impedância:
I =
V
Z
I =
220V
54,46Ω
ou I =4,04 ∠0° A .
Triângulo das Tensões (Fig. 16-17)
Queda de tensão sobre o resistor:
VdR =IR VdR =4,04 x 50 VdR =202∠ 0° V
Queda de tensão sobre o indutor:
VdL = I (XL) VdL =4,04( j 22,62)
VdL =91,285∠90° V .
Queda de tensão sobre o capacitor:
12

13. Análise de circuitos elétricos CC e CA Pedro Barros Neto
VdC = I (−jXC) VdC =4,04(− j44,2) VdC = 178,568∠−90°V .
Queda de tensão equivalente sobre os elementos reativos:
Vd XEQ = jVdL−j VdC Vd XEQ= j 91,285− j178,568 ou Vd XEQ =− j 87,283V .
Queda de tensão na carga: V dEQ =VdR − jVd XEQ ou V dEQ =202− j 87,28 V . Na forma
polar V d XEQ=√2022
+ 87,282
tg−1
[−87,28
202 ] VdEQ =220∠−23,37° V adequar o ângulo
para − j com a m.d.p. VdEQ =220∠336,63° V .
Elevação de tensão total na fonte, com o módulo da corrente: V r =−[I .Z] . Na forma
retangular V r =−[4,04(50− j21,6)] ou V r =−202 + j 87,264 V . Na forma polar
V r =√202
2
+ 87,264
2
tg
−1 87,264
−202
V r =−220∠−23,36° adequar o ângulo para + j com
o simétrico V r =−220∠156,63° V .
Triângulo das potências (Fig. 16.18):
Potência no resistor:
P=I ² R P= 4,04
2
x50 ou P= 816,08W .
Potência reativa no Indutor:
QL = jVdL x I QL = j 91,285x 4,04
QL = j368.79VAR . Na forma polar
QL =368.79∠ 90° VAR .
Potência reativa no Capacitor:
QC =− jVdC x I QC =− j178,568 x 4,04
QC =− j721,41VAR na forma polar
QC =721,41∠−90°VAR .
Potência Reativa equivalente: QEQ = jQL− jQC Qt = j 368,79− j721,41
QEQ =− j 352,62VAR na forma polar QEQ = 352,62∠−90°VAR com predominância
capacitiva.
Potência total na forma retangular S= P− jQEQ S=816,08− j 352,62 . Na forma polar
S= S ∠m.d . p.(−ϕ ) onde o módulo , ou potência aparente, será S =√P²+Q ²
S =√816²+352,6² ou S =889VA . Então, S=889∠336,63° VA .
13

14. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Potência total fornecida pela fonte com o módulo da corrente: Sf =V EQ I . Na forma
retangular Sf =(−202+ j 87,28)4,04 ou Sf =−816 + j 352,6 VA onde P=−816,08W e
QEQ = j352,6VAR . Na forma polar Sf =−S∠ϕ ou Sf =−889∠336,63° VA .
Fator de potência
FP=cos ϕ cos336,63° =0,9187
Neste exemplo o FP é excelente, pois 92 % da energia é gasta sobre o resistor, enquanto apenas
8 % é trocada entre a fonte e as reatâncias.
Ressonância deste circuito
• f0 =
1
2 π √LC
(Hz). f 0 =
1
6,28√0,06 x0,00006
f 0 =
1
6,28 x 0,00189
f 0 =
1
0,0119
f 0 =89,29Hz .
• A impedância do circuito terá o menor valor Z =R ou Z =50Ω∠0°
• A corrente eficaz será máxima: I =
220
50
I =4,4 A .
• A queda de tensão no resistor é dada por VdR =IR .
• Fator de qualidade Q=
1
R √L
C
Q =
1
50 √ 0,06
0,00006
Q =0,02√1 Q =0,02 .
• Banda passante Δ f =
f 0
Q
Δ f =
89,29
0,02
Δ f = 4.464 Hz muito larga, com
seletividade muito baixa em f 0 .
16.6.4 - Exemplo (fig. 16 – 19)
14

15. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Dados Vf =150 ∠0°V o módulo da tensão está como referência de fase. R=12Ω
XL = j 20Ω XC =− j16Ω . Notar que as reatâncias já estão convertidas do domínio do
tempo para o domínio fasorial, para uma determinada frequência da fonte, que não é informada.
Impedância complexa : Z=R + jL − jC Z=12 +( j20− j 16) Z=12 + j 4 Ω , onde
j 4 é a reatância equivalente. Na notação polar Z =√12
2
+ 4
2
tg
−1
( 4
12) ou
Z=12,65 ∠18,43° Ω , com predominância indutiva.
O fasor do módulo da impedância está na mesma reta suporte do módulo da tensão, portanto, a
impedância, com predominância indutiva, estará adiantada 18,43° da corrente. Isso significa
que os fasores Reais: da corrente eficaz, da resistência e da potência eficaz estarão defasados com
atraso, em relação ao módulo da tensão total, de –18,43° , que convertidos para a m.d.p. ficarão
em 341,57° .
LTK da malha com os módulos das tensões: Vf ∠ 0° =VdEQ ∠0° .
Corrente da malha: com o módulo da queda de tensão na carga I =
VdEQ
ZEQ
. Na forma retangular
I =
150
12 + j 4
ou I =11,25−j 3,75 A .
Na forma polar I =
150
12,65∠18,43°
I =11,8577∠−18,43° A ou I =11,86∠341,57° A .
Outra maneira para calcular a forma retangular: I =11,86(cos341,57°)+ j 11,86(sen341,57°)
I =11,86(0,949)+ j 11,86(−0,316) ou I =11,25− j 3,75 A .
Este circuito tem predominância indutiva, com a tensão adiantada 18,43° em relação à corrente.
Queda de tensão nas impedâncias:
15

16. Análise de circuitos elétricos CC e CA Pedro Barros Neto
V dR =R(I) V dR =12(11,25 − j3,75) V dR =(135− j 45)V . Na forma polar, o módulo
será VdR =√135
2
+ 45
2
e então, teremos V dR =142,3∠341,57° V .
V dL = XL. I V dL = j 20(11,25− j 3,75) V dL =(75 + j225)V . Na forma polar
V dL =√752
+ 2252
tg−1
(225
75 ) ou V dL =237∠71,57°V .
V dC = XC .I V dL =− j16(11,25− j 3,75) V dC =(−60− j 180)V . Na forma polar
V dC =√602
+ 1802
tg−1
(−180
−60 ) V dC =189,73∠ 71,58° V adequar o ângulo para −j com
a m.d.p. V dC =189∠251,58° V .
Queda de tensão reativa equivalente V dXEQ =V dL −V dC . Na forma retangular
V dXEQ =(75 + j225)−60− j180 ou V dXEQ =15 + j 45V . Na forma polar
V dXEQ = √15
2
+ 45
2
tg
−1
(45
15) ou V dXEQ =47,434∠71,57° .
Queda de tensão total no circuito V d = I Z Vd =(11,25−j 3,75)(12+ j 4) na forma polar
V d =150∠0° .
Elevação da tensão total na fonte: V r =−V d V r =−150∠ 0° . Apenas o módulo é
simétrico, com o mesmo ângulo da queda de tensão total no circuito.
Detalhamento da LTK: V dR + V dL +V dC −V r =0 ou
(135− j 45)+(75 + j 225)−(60− j180)−(150 + j 0)=0 .
16

17. Análise de circuitos elétricos CC e CA Pedro Barros Neto
Potências
Potência eficaz com o módulo da corrente total: P=(I2
∠ϕ )R P =(11,862
∠−18,43°)(12)
P=1.687,9∠−18,43° W ou P =1.688∠341,57° W .
Potência reativa indutiva com módulo da corrente total: QL =(I
2
∠ϕ )( jX L)
QL =(11,86
2
∠−18,43°)( j20) QL =2.813,2∠−18,43°+90° ou
QL =2.813,2∠71,57° VAR .
Potência reativa capacitiva com módulo da corrente total: QC =(I
2
∠ϕ )(− jXC )
QC =(11,862
∠−18,43°)(− j16) QC =−2.250,55∠−18,43°−90°
QC =2.250,55∠−108,43° adequar o ângulo para −j com a m.d.p.
QC =2.250,55∠251,57° VAR .
Potência reativa equivalente com módulo da corrente total: QEQ =(I
2
∠ϕ )( jXEQ)
QEQ =140,66∠−18,43°( j 4) QEQ =562,64∠−18,43°+90° ou QEQ =562,64∠71,57° .
Potência total na carga:
Forma retangular S= P∠ϕ + Q(ϕ + j) ou S=1.688∠341,57° + 562,64∠71,565° VA .
Forma polar S =√1.688
2
+562,5
2
tg
−1
[562,64
1.687,9] , então S= 1.778,78∠18,435° VA . Como
o módulo da potência total está na mesma reta suporte do módulo da tensão total, que é a referência
de fase Vf ∠ 0° ou 18,43° =0ω t rad . Portanto, a corrente e a potência eficaz estão
atrasadas –18,43° , que convertidos para a m.d.p. ficarão em 341,57° .
Potência total na fonte Sf =Vr .I
∗
. Na forma retangular Sf =−150(11,25 + j3,75) ou
Sf =−1.688− j 562,6 VA , onde P =−1.688∠341,57° W e
QEQ =−j 562,6∠71,565° VAR . Na forma polar Sf =−1.778,78∠18,435° VA . Apenas o
módulo é simétrico, com o mesmo ângulo da potência total consumida no circuito.
17