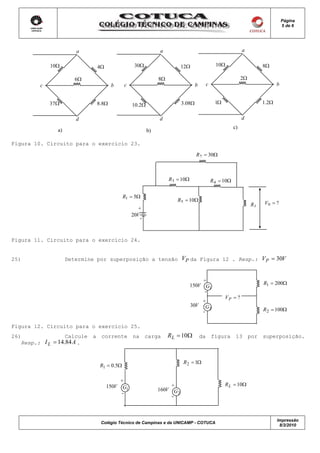
Este documento contém 30 exercícios sobre circuitos elétricos. Os exercícios avaliam conceitos como corrente elétrica, tensão, resistência e métodos para análise de circuitos como método das malhas, método nodal e superposição. Os alunos devem resolver os exercícios utilizando estas ferramentas de análise de circuitos elétricos.

1. Página
1 de 6
CURSO Eletroeletrônica - DATA ___ / ___ / ___
COMPONENTE Eletricidade Básica
ALUNO N°
DOCENTE Prof. Romeu Corradi Júnior [www.corradi.junior.nom.br]
Assunto: Lista de Exercícios – Revisão geral
OBSERVAÇÃO: Esta lista de exercícios avalia o conteúdo ministrado em sala de aula e o
conteúdo descrito nos capítulos 1, 3, 4, 5, 7 e 8 do livro texto: ELETRICIDADE BÁSICA,
Milton Gussow.
1) Mostre a estrutura atômica do elemento neon, que tem número atômico igual a 10. Qual a
sua valência. Resp: o neon é inerte
2) O que resulta do átomo de silício (número atômico= 14) quando dele se retiram todos os
elétrons que orbitam na sua camada mais externa?
3) Um isolante carregado possui um excesso de 25× 1018 elétrons. Determine a sua carga em
coulombs com a respectiva polaridade. Resp: Q=-4 C
4) Um material com excesso de 25× 1018 elétrons perde 6,25 × 1018 elétrons. Faz-se com que os
elétrons excedentes fluam passando por um dado ponto em 2s. Calcule a corrente
produzida pela passagem dos elétrons resultantes. Resp: 1.5 A.
5) Calcule a tensão necessária para que uma corrente de 10 A circule pelo circuito série
da figura 1 abaixo. Resp: 100V.
R1 = 2Ω
I = 10 A
VT = ? R 2 = 3Ω
R3 = 5Ω
Figura 1. Circuito para o exercício 5.
6) Na figura 2, uma bateria de 12V fornece uma corrente de 2 A. Se R 2 = 2Ω calcule R1 e V1 .
Resp: R1 = 4Ω e V1 = 8V .
V1
R1
I = 2A
VT = 12V
R 2 = 2Ω
Figura 2. Circuito para o exercício 6.
7) Um circuito série Figura 3 utiliza o terra como uma ligação comum e como um ponto de
referência para as medidas de tensão (a ligação terra está em 0 V). Marque a polaridade
Impressão
Colégio Técnico de Campinas e da UNICAMP - COTUCA
8/3/2010

2. das quedas de tensão através das resistências R1 e R 2 e calcule as quedas de tensão nos
pontos A e B com relação à terra. Resp V A = 50V e V B = 50V .
VT = 100V
B A
R 2 = 100Ω R1 = 100Ω
Figura 3. Circuito para o exercício 7.
8) Um circuito CC transistorizado pode ser representado como na Figura 4. Calcule a
resistência total e a tensão entre os pontos A e B. Resp.: RT = 50kΩ e V AB = 30V .
A
I L = 0.6mA R L = 12kΩ
RCB = 13kΩ
I =0
R E = 25kΩ
B
Figura 4. Circuito para o exercício 8.
9) Um “spot” de teatro de 12 Ω está ligado em série com um resistor regulador de 32 Ω
(Figura 5). Se a queda de tensão através da lâmpada for de 31.2 V calcule os valores
que estão faltando indicados na figura. Resp.: I 1 = I 2 = I = 2.6 A , V 2 = 83 .2V , VT = 114.4V ,
RT = 44Ω .
spot
V1 = 31.2V
I =? I I1 = ? I2 = ?
VT = ? R1 = 12Ω V2 = ?
RT = ? R 2 = 32Ω
Figura 5. Circuito para o exercício 9.
10) Calcule os valores de tensão que aparecem nos pontos A, B C e D em relação
à terra na figura 6. Resp.: V A = 60V , V B = 50V , VC = 30V , V D = 0V
11) Dois resistores formam um divisor de tensão para polarização de base num
amplificador de áudio. As quedas de tensão através deles são de 2.4 V e 6.6 V
respectivamente, em um circuito de 1.5mA. Determine a potência de cada resistor e a
potência total dissipada em miliWatts. Resp.: P = 3.6mW , P2 = 9.9mW , PT = 13.5mW .
1

3. Página
3 de 6
A R1 = 5Ω
B
60V R 2 = 10Ω
D C
R3 = 15Ω
Figura 6. Circuito para o exercício 10.
12) Um potenciômetro pode ser considerado como um divisor simples de tensão
com dois resistores (ver figura 7). Em que ponto da resistência deve ser colocado o
braço de controle de um potenciômetro de 120 ohms para se obter 2.5 V entre o braço
(ponto A) do potenciômetro e o terra (ponto B). Resp.: no ponto de 25 ohms a partir do
terra.
+ A
12V 2.5V
_
B
Figura 7. Circuito para o exercício 12.
13) Os ramos de circuito de um sistema de fiação doméstica são paralelos.
Liga-se ao circuito da cozinha uma torradeira, uma cafeteira, e um ferro elétrico,
sendo a tensão aplicada de 110V. Calcule (a) a corrente total que supre as cargas; (b)
a tensão em cada aparelho; (c) a resistência total do circuito. São dados a corrente na
torradeira, que vale 8.3 A, a corrente através da cafeteira, que vale 8.3 A e a
corrente através do ferro elétrico, que vale 9.6 A. Resp.: I T = 26.2 A , V1 = V2 = V3 = 110V
, RT = 4.2Ω .
14) Duas resistências ( R1 = 72kΩ e R2 = 18kΩ ) estão associadas em paralelo e
são supridas através de uma corrente total de 30 mA. Calcule a corrente em cada
resistência. Resp.: I1 = 6mA e I 2 = 24mA .
15) A resistência total associada a uma cafeteira elétrica e uma torradeira é
de 24 ohms. Calcule a potência total associada consumida pelo aparelhos se a tensão de
alimentação é de 120V. Resp.: PT = 600W .
16) Um amperímetro (um instrumento que mede corrente) conduz uma corrente
elétrica de 0.05A e está em paralelo com um resistor em derivação que conduz 1.9 A. Se
a tensão através da associação é de 4.2 V, calcule (a) a corrente total (b) a
resistência de derivação (c) a resistência do amperímetro e (d) a resistência total do
circuito. Resp.: a) I T = 1.95 A ; b) R = 2.21Ω ; c) R A = 84Ω ; d) RT = 2.15Ω ;
Impressão
Colégio Técnico de Campinas e da UNICAMP - COTUCA
8/3/2010

4. 17) A bobina de ignição e o motor de partida de um carro estão ligados em
paralelo através de uma bateria de 12V por meio de uma chave de ignição. Sabendo-se que
a corrente na bobina de ignição é de 5 A e que a corrente no motor é de 100A, calcule
(a) a corrente total retirada da bateria; (b) a tensão através da bobina e do motor (c)
a resistência total do circuito. Resp.: a) I T = 105 A ; b) V1 = V2 = 12V ; c) RT = 0.114Ω ;
18) Cinco lâmpadas de 150 W estão ligadas em paralelo a uma linha de 120V. Se
um filamento se abrir, quantas lâmpadas se manterão acesas? Resp.:Quatro.
19) Calcule todas as correntes através das resistências da Figura 8, pelo
método das correntes de malha. Resp.: I1 = 3 A , I 2 = 1A , I1 − I 2 = 2 A (corrente no resistor
2).
R1 = 4Ω R 4 = 1Ω
I1 I2
VT = 25V R 2 = 5Ω R5 = 6Ω
R3 = 1Ω R6 = 3Ω
Figura 8. Circuito para o exercício 19.
20) Resolva o exercício anterior pelo método das tensões nodais.
21) Calcule todas as correntes e quedas de tensão na Figura 9 pelo método das
tensões nodais. Recalcule utilizando o método das correntes de malha. Resp.: I1 = 5 A ,
I 2 = −1A , I 3 = 4 A , V1 = 60V , V2 = 24V , V3 = 3V .
R1 = 4Ω R3 = 3Ω
+ I1 I2 +
84V R 2 = 6Ω 21V
- -
I3
Figura 9. Circuito para o exercício 21.
22) Resolva o exercício anterior pelo método da superposição.
23) Calcule a resistência de entrada entre os terminais a e d para as redes
dadas em (a) (b) e (c) na Figura 10. Se aplicarmos 50V nos terminais do circuito da
Figura 10c, qual será a corrente em cada resistor? Resp.: a) RT = 10Ω , b) RT = 11Ω , c)
RT = 5Ω . I ac = 4.5 A , I cd = 5 A , I ab = 5.5 A , I cb = 0.5 A , I bd = 5 A .
24) Calcule a resistência equivalente e a tensão de saída V0 na rede da
Figura 11. Resp.: RT = 25Ω , V0 = 7.5V .

5. Página
5 de 6
a a a
10Ω 4Ω 30Ω 12Ω 10Ω 8Ω
6Ω 8Ω 2Ω
c b c b c b
37Ω 8.8Ω 10.2Ω 3.08Ω 1Ω 1.2Ω
d d d
c)
a) b)
Figura 10. Circuito para o exercício 23.
R 2 = 30Ω
R3 = 10Ω R 4 = 10Ω
R1 = 5Ω
R5 = 10Ω
RL V0 = ?
+
20V
-
Figura 11. Circuito para o exercício 24.
25) Determine por superposição a tensão VP da Figura 12 . Resp.: V P = 30V
+ R1 = 200Ω
150V G1
-
VP = ?
+
30V G
-
2 R 2 = 100Ω
Figura 12. Circuito para o exercício 25.
26) Calcule a corrente na carga RL = 10Ω da figura 13 por superposição.
Resp.: I L = 14.84 A .
R 2 = 1Ω
R1 = 0.5Ω
+
150V + R L = 10Ω
G1 160V G
- 2
-
Impressão
Colégio Técnico de Campinas e da UNICAMP - COTUCA
8/3/2010

6. Figura 13. Circuito para o exercício 26.
27) Calcule a corrente e a tensão na carga RL . Resp.: I L = 2 A , V L = 20V .
R1 = 1Ω
+
50V R 2 = 5Ω RL
-
R3 = 4Ω
Figura 14. Circuito para o exercício 27.
28) Uma fonte de tensão de 24 V está em série com uma resistência de 6 ohms.
Desenhe o circuito Norton equivalente. Resp.: I N = 4 A , R N = 6Ω .
29) Dada a figura 15, (a) mostre o equivalente Thévenin e calcule V L ; (b)
Determine V L por superposição; (c) Calcule V L pelo teorema do equivalente de Norton.
Resp.: RTh = 3Ω , VTh = 22.5V . V L = 18V .
a
R1 = 4Ω
R L = 12Ω
R 2 = 12Ω
+
+
V1 = 20V
- - V 2 = 30V
b
Figura 15. Circuito para o exercício 29.
30) Calcule a corrente através do resistor de carga R L = 4Ω na Figura 16.
Resp.: I L = 0.2 A .
5A R1 = 2Ω
R L = 4Ω
2A
R 2 = 4Ω
Figura 16. Circuito para o exercício 30.