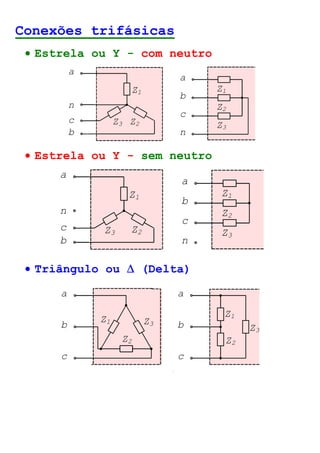
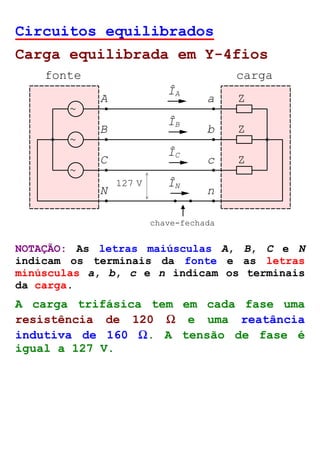
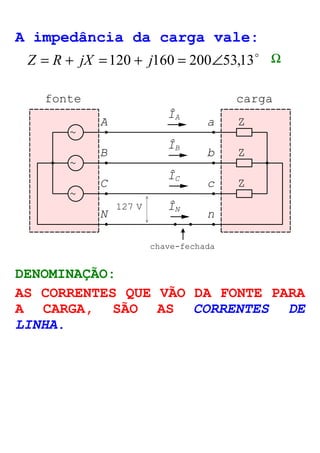
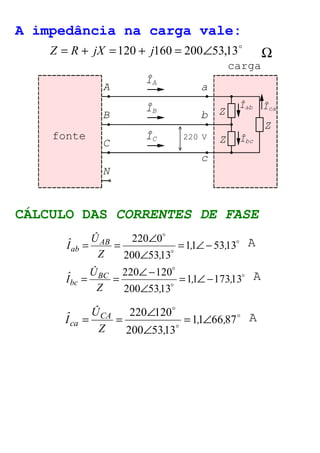
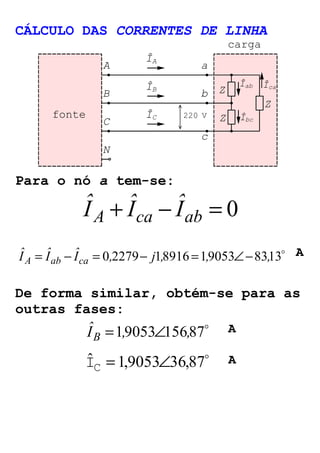
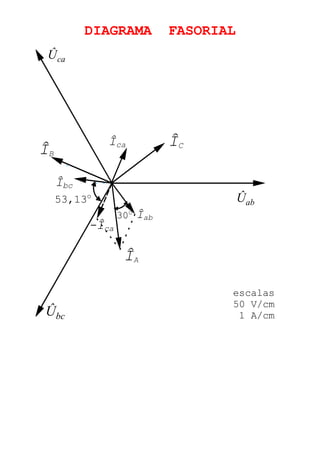
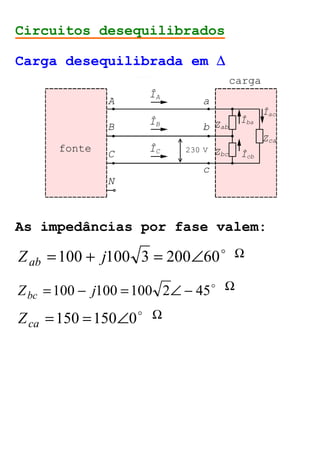
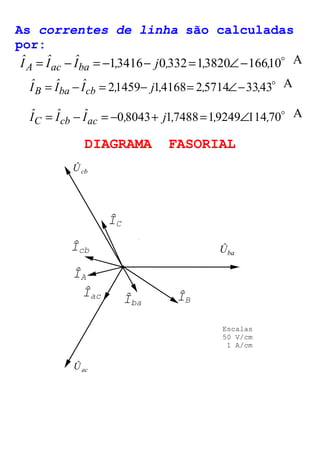
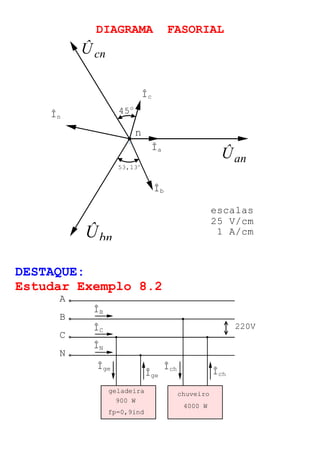
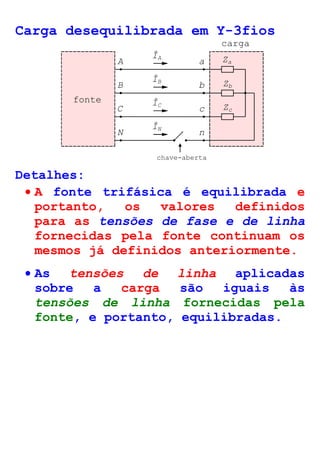
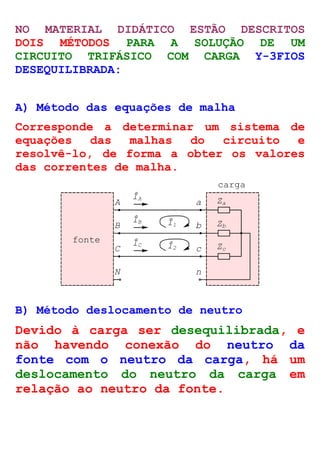
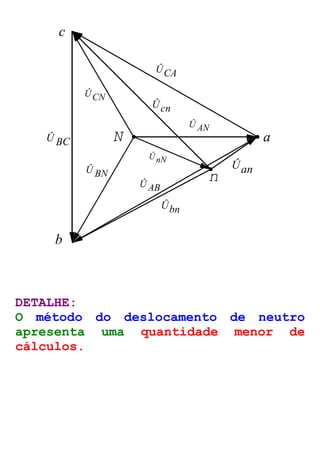
O documento descreve circuitos trifásicos equilibrados e desequilibrados. Apresenta as tensões e correntes de fase e linha em fontes trifásicas, além de conexões trifásicas como estrela e triângulo. Explica como calcular tensões, correntes e diagramas fasoriais para cargas equilibradas e desequilibradas nas conexões estrela e triângulo.

1. Capítulo 8
Circuitos Trifásicos
Fonte de tensões trifásicas
REPRESENTAÇÃO DE UMA FONTE TRIFÁSICA
A
B
C
N
Û
Û
Û
Û
Û
Û
~
~
~
CA AB
BC
CN
BN
AN
DENOMINAÇÃO:
OS CONDUTORES A B e C SÃO AS FASES
O CONDUTOR CONECTADO NO PONTO N É O
NEUTRO

2. DENOMINAÇÃO: TENSÃO DE FASE
É a tensão entre cada fase e o neutro.
NOTAÇÃO: A letra maiúscula sem acento
corresponde ao valor eficaz, e, a letra
maiúscula com acento circunflexo corres-ponde
ao fasor da grandeza elétrica.

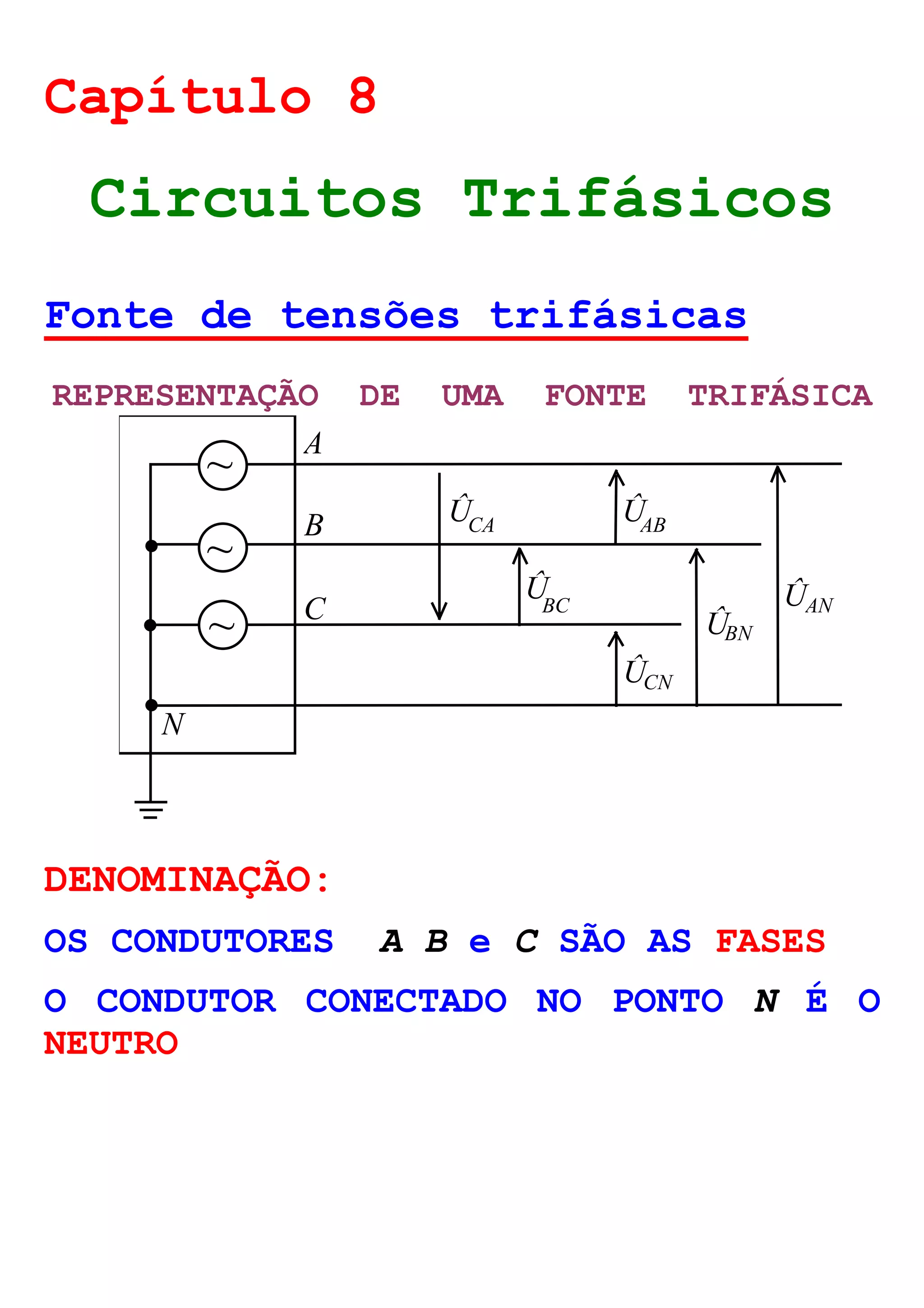
3. TENSÕES DE FASE
uAN(t) uBN(t) uCN(t)
wt [rad]
2p/3 4p/3 2p
o
ÛAN =UÐ0
V
o
ÛBN =UÐ-120
V
o o
ÛCN =UÐ- 240 =UÐ120
V

4. TENSÕES DE FASE
QUAL A DIFERENÇA?
uAN(t) uBN(t) uCN(t)
wt [rad]
2p/3 4p/3 2p
uAN(t)
wt[rad]
uCN(t) uBN(t)
2p/3 4p/3 2p

5. Seqüência de fases ABC
o
ÛAN =UÐ0
V
o
ÛBN =UÐ-120
V
o o
ÛCN =UÐ- 240 =UÐ120
V
Seqüência de fases ACB
o
ÛAN =UÐ0
V
o o
ÛBN =UÐ- 240 =UÐ120
V
o
ÛCN =UÐ- 120
V

6. Exemplo 8.1
Qual seria o valor da tensão medida por
um voltímetro conectado aos terminais A
e B da fonte?
A
B
C
N
ÛAB v
Û
Û
Û
~
~
~
CN
BN
AN
Solução:
Aplicação da lei das tensões de
Kirchhoff:
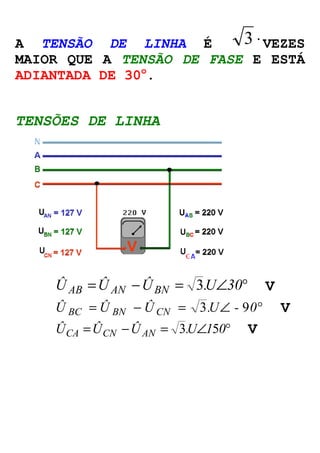
( ) ÛAB =ÛAN -ÛBN =ÛAN + -ÛBN



+ = 



1
= Ð - Ð - = - - -

3
2
j
3
2
U
3
2
j
2
o o
ÛAB U 0 U ( 120 ) U U
[ o o ] o 3 U cos30 jsen30 3 U 30
1
j

ÛAB 3 U = × 
+ = × Ð 2
3
= × +
2


V

7. Û = 3 ×UÐ30o AB
V
DENOMINAÇÃO: TENSÃO DE LINHA
Corresponde à tensão entre duas
fases.
- ÛBN
ÛAB
ÛBN
Û AB
B
30o
A
Û AN
N
Obtenção gráfica de ÛAB

8. A TENSÃO DE LINHA É 3 ×VEZES
MAIOR QUE A TENSÃO DE FASE E ESTÁ
ADIANTADA DE 30o.
TENSÕES DE LINHA
ÛAB =ÛAN -ÛBN = 3.UÐ30° V
Û BC = Û BN - ÛCN = 3.UÐ - 90° V
ÛCA =ÛCN -ÛAN = 3.UÐ150° V

9. CONVENÇÃO:
a) Para a seqüência de fases ABC:
Observando esta notação
Ç Ç Ç
AB BCCA
as tensões de linha são denotadas por:
ÛAB ÛBC ÛCA
b) Para a seqüência de fases ACB:
Observando esta notação
Ç Ç Ç
ACCB BA
as tensões de linha são denotadas por:
ÛAC ÛCB ÛBA

10. DIAGRAMA FASORIAL
AN
Û
Û AB
CN
CA
ÛB N
Û
Û
ÛB C
300
1200
1200
0o
Qual é a seqüência de fases?
Convenção: considerar sentido de
giro dos fasores anti-horário e
observar o giro dos fasores a partir
da referência 0o

11. Conexões trifásicas
· Estrela ou Y - com neutro
a
b
c
n
Z1
Z2
Z3
a
Z1
Z3 Z2
n
c
b
· Estrela ou Y - sem neutro
a
b
c
n
Z1
Z2
Z3
a
Z1
Z3 Z2
n
c
b
· Triângulo ou D (Delta)
D
Z1
Z2
Z3
a
b
c
a
b
c
Z1
Z2
Z3

12. Se as três impedâncias da carga
forem iguais (Z1=Z2=Z3), a carga é
denominada equilibrada.
Caso contrário, a carga trifásica
é considerada desequilibrada.
Na prática:
Todas as fontes trifásicas são
equilibradas.
Assim, um circuito trifásico é
considerado equilibrado se a carga
for equilibrada e o circuito será
desequilibrado se a carga for
desequilibrada.

13. Circuitos equilibrados
Carga equilibrada em Y-4fios
fonte carga
~
~
~
ÎA
A a Z
ÎB
B b
Z
ÎC
C c Z
N
n
127 V ÎN
chave-fechada
NOTAÇÃO: As letras maiúsculas A, B, C e N
indicam os terminais da fonte e as letras
minúsculas a, b, c e n indicam os terminais
da carga.
A carga trifásica tem em cada fase uma
resistência de 120 W e uma reatância
indutiva de 160 W. A tensão de fase é
igual a 127 V.

14. Considerando a seqüência de fases
ABC e a tensão de fase ÛAN como
referência angular, as tensões de
fase fornecidas pela fonte são
iguais a:
TENSÕES DE FASE
= = 127Ð0o Ûan ÛAN V
o = = 127Ð-120 Ûbn ÛBN V
o = = 127Ð120 Ûcn ÛCN V
TENSÕES DE LINHA
Ûab = .127Ð30° = Ð30° 3 220 V
Ûbc = 3.127Ð- 90° = 220Ð- 90° V
Ûca = .127Ð1 0° = Ð1 0° 3 5 220 5 V

15. A impedância da carga vale:
Z = R + jX =120 + j160 = 200Ð53,13o W
fonte carga
~
~
~
ÎA
A a Z
ÎB
B b
Z
ÎC
C c Z
N
n
127 V ÎN
chave-fechada
DENOMINAÇÃO:
AS CORRENTES QUE VÃO DA FONTE PARA
A CARGA, SÃO AS CORRENTES DE
LINHA.

16. CÁLCULO DAS CORRENTES DE LINHA
o
= = Ð
Iˆ an
A = Ð-
o
o
0 635 5313
127 0
Ð
200 5313
, ,
Û
Z ,
A
o
o
= = Ð-
127 120
Iˆ bn
B = Ð-
o
0 635 17313
Ð
200 5313
, ,
Û
Z ,
A
o
= = Ð
Iˆ cn
C = Ð
o
o
0 635 66 87
127 120
Ð
200 5313
, ,
Û
Z ,
A
DIAGRAMA FASORIAL
n
Û an
Ûcn
53,13o
53,13o
53,13o
Ûbc
escalas
30 V/cm
0,5 A/cm
Û ca
Û ab
Ûbn
ÎA
ÎB
ÎC

17. Carga equilibrada em D
B
C
b
c
N
carga
ÎA
A a
ÎB
ÎC
Z
Z
Z
Îab
Îbc
Îca
fonte 220 V
DENOMINAÇÃO:
AS CORRENTES QUE CIRCULAM NA
IMPEDÂNCIA DA CARGA, SÃO AS
CORRENTES DE FASE.
Convenção para o sentido das
correntes de fase:
a) Para a seqüência de fases ABC:
Ç Ç Ç
AB BC CA ⇒ Îab Îbc Îca
b) Para a seqüência de fases ACB:
Ç Ç Ç
AC CB BA ⇒ Îac Îcb Îba

18. B
C
b
c
N
carga
ÎA
A a
ÎB
ÎC
Z
Z
Z
Îab
Îbc
Îca
fonte 220 V
A carga trifásica tem em cada fase
uma resistência de 120 W e uma
reatância indutiva de 160 W. A
tensão de linha é igual a 220 V.
Considerando a seqüência de fases
ABC e a tensão de linha ÛAB como
referência angular, as tensões de
linha fornecidas pela fonte são
iguais a:
= 220Ð0° AB Û
V
Û = 220Ð-120° BC
V
= 220Ð120° CA Û
V

19. A impedância na carga vale:
Z = R + jX =120 + j160 = 200Ð53,13o W
B
C
b
c
N
carga
ÎA
A a
ÎB
ÎC
Z
Z
Z
Îab
Îbc
Îca
fonte 220 V
CÁLCULO DAS CORRENTES DE FASE
o
= = Ð
Iˆ AB
ab = Ð-
o
o
11 5313
220 0
Ð
200 5313
, ,
Û
Z ,
A
o
o
= = Ð-
220 120
Iˆ BC
bc = Ð-
o
11 17313
Ð
200 5313
, ,
Û
Z ,
A
o
= = Ð
Iˆ CA
ca = Ð
o
o
11 66 87
220 120
200 5313
, ,
Û
Z ,
Ð
A

20. CÁLCULO DAS CORRENTES DE LINHA
B
C
b
c
N
carga
ÎA
A a
ÎB
ÎC
Z
Z
Z
Îab
Îbc
Îca
fonte 220 V
Para o nó a tem-se:
IˆA + Iˆca - Iˆab = 0
o Iˆ Iˆ Iˆ 0,2279 j1,8916 1,9053 83,13
A = ab - ca = - = Ð- A
De forma similar, obtém-se para as
outras fases:
o Iˆ 1,9053 156,87
B = Ð
A
o ˆ = 1,9053Ð36,87 IC
A

21. DIAGRAMA FASORIAL
escalas
50 V/cm
1 A/cm
Ûca
Ûbc
Îab
Îca
ÎA
ÎB
ÎC
53,13o
30o
Îbc
-Îca
Ûab

22. Relação entre corrente de linha e
corrente de fase:
o
= Ð-
19053 , 8313 ,
= Ð-
o
o
3 30
Ð-
11 , 5313
,
Iˆ
ab
Iˆ
A
A CORRENTE DE LINHA É 3 VEZES
MAIOR QUE A CORRENTE DE FASE E
ESTÁ ATRASADA DE 30O.
LINHA IFASE Iˆ = 3 × ˆ
ATENÇÃO:
Esta relação é válida somente
para carga D-equilibrada.

23. Circuitos desequilibrados
Carga desequilibrada em D
B
b
ÎA
C c
N
carga
A a
ÎB
ÎC
ÎA
Zca
Zab
Zbc
Îab
Îca
Îbc
fonte
+
230V
-
B
C
b
c
N
carga
A a
ÎB
ÎC
Zca
Zab
Zbc
Îba
Îcb
Îac
fonte 230 V
As impedâncias por fase valem:
Z ab
=100 + j100 3 = 200Ð60o W
o Zbc =100 - j100 =100 2Ð - 45
W
o Zca =150 =150Ð0
W

24. Para a seqüência de fases ACB e
assumindo a tensão de linha Ûba como
referência angular, as tensões de
linha valem:
Ûba = 230Ð0°
V
Ûcb = 230Ð120°
V
Ûac = 230Ð-120°
V
As correntes de fase são iguais a:
o
o
= = Ð ,
Z
230 0 = Ð-
Ð
o
115 60
200 60
Û
Iˆ
ba
ab
ba
A
o
= = Ð ,
Z
230 120 = Ð
o
o
1 6263 165
Ð-
100 2 45
Û
Iˆ
cb
bc
cb
A
o
230 Ð- 120 o
= = = , Ð-
Z
15333 120
150
Û
Iˆ
ac
ca
ac
A

25. As correntes de linha são calculadas
por:
Iˆ Iˆ Iˆ 1,3416 j0,332 1,3820 166,10o
A = ac - ba = - - = Ð-
A
o Iˆ Iˆ Iˆ 2,1459 j1,4168 2,5714 33,43
B = ba - cb = - = Ð-
A
o Iˆ Iˆ Iˆ 0,8043 j1,7488 1,9249 114,70
C = cb - ac = - + = Ð
A
DIAGRAMA FASORIAL
Escalas
50 V/cm
1 A/cm
Ûcb
ÎA
ÎB
ÎC
Îba
Îcb
Îac
Ûba
Ûac

26. Carga desequilibrada em Y-4 fios
ÎA
B b
Zb
C c Zc
N
100 V
chave-fechada
carga
A a Za
ÎB
ÎC
ÎN
fonte
n
As impedâncias da carga por fase valem:
=100 =100Ð0o Za
W
o Zb = 30 - j40 = 50Ð - 53,13
W
o Zc = 50 + j50 = 50 2Ð45
W
Considerando a tensão de fase ÛAN
como referência angular tem-se:
o Ûan =100Ð0
V
o Ûbn =100Ð-120 V
o Ûcn = 100Ð120 V

27. As correntes de linha valem:
o
= = 100 Ð 0 o
= , Ð
1 0 0
100
Û
an
Z
Iˆ
a
A
A
o
o
= = Ð-
B = Ð-
o
2 66 87
100 120
50 5313
,
Û
bn
Z ,
Iˆ
b
Ð-
A
o
= = Ð o
,
100 120 = Ð
o
1 4142 75
Ð
50 2 45
Û
cn
Z
Iˆ
c
C
A
Corrente no condutor neutro:
Aplica-se a lei de nós de Kirchhoff
para o ponto neutro da carga: ( ) ÎN = - ÎA + ÎB + ÎC
o Î -2,1516 j0,4732 2,2030 167,60 N = + = Ð A

28. DIAGRAMA FASORIAL
n
45o
53,13o
Ûan
Ûcn
Ûbn
Îa
Îb
Îc
În
escalas
25 V/cm
1 A/cm
DESTAQUE:
Estudar Exemplo 8.2
geladeira
900 W
fp=0,9ind
chuveiro
4000 W
ÎB
ÎC
ÎN
A
B
Îch
Îch
C
N
Îge Îge
220V

29. Carga desequilibrada em Y-3fios
ÎA
B b
Zb
C c Zc
N
n
chave-aberta
carga
A a Za
ÎB
ÎC
ÎN
fonte
Detalhes:
· A fonte trifásica é equilibrada e
portanto, os valores definidos
para as tensões de fase e de linha
fornecidas pela fonte continuam os
mesmos já definidos anteriormente.
· As tensões de linha aplicadas
sobre a carga são iguais às
tensões de linha fornecidas pela
fonte, e portanto, equilibradas.

30. · No entanto, devido ao fato de que
o neutro da carga n e o da fonte N
não estão conectados, há uma
diferença de potencial entre esses
dois pontos, devido ao desequi-líbrio
da carga trifásica, levando
à conclusão de que as tensões de
fase aplicadas à carga não são
iguais às tensões de fase forne-cidas
pela fonte.
· Devido à não conexão dos
neutros, a corrente no neutro é
nula.
· Aplicando a lei dos nós de
Kirchhoff para o ponto neutro da
carga, tem-se:
Î A + ÎB + ÎC = 0

31. NO MATERIAL DIDÁTICO ESTÃO DESCRITOS
DOIS MÉTODOS PARA A SOLUÇÃO DE UM
CIRCUITO TRIFÁSICO COM CARGA Y-3FIOS
DESEQUILIBRADA:
A) Método das equações de malha
Corresponde a determinar um sistema de
equações das malhas do circuito e
resolvê-lo, de forma a obter os valores
das correntes de malha.
B b
Zb
C c Zc
N n
carga
A a Za
fonte
ÎA
ÎB
ÎC
Î1
Î2
B) Método deslocamento de neutro
Devido à carga ser desequilibrada, e
não havendo conexão do neutro da
fonte com o neutro da carga, há um
deslocamento do neutro da carga em
relação ao neutro da fonte.

32. n
N
Ûan
ÛnN
Ûbn
ÛCN
ÛBN
ÛAB
ÛBC
ÛCA
Ûcn
ÛAN
c
b
a
DETALHE:
O método do deslocamento de neutro
apresenta uma quantidade menor de
cálculos.

33. O método do deslocamento de neutro
baseia-se em obter a diferença de
potencial entre os pontos neutros e,
em seguida, as demais tensões e
correntes.
× + × + ×
Y Û Y Û Y Û
a AN b BN c CN
nN Y Y Y
a b c
Û
+ +
=
Ya , Yb e Yc - admitâncias da carga
São calculadas através do inverso das


Z
respectivas impedâncias 

1
.
Tendo-se ÛnN , pode-se então obter as
tensões de fase na carga:
Ûan =ÛAN -ÛnN
Ûbn = ÛBN -ÛnN
Ûcn = ÛCN -ÛnN
e tendo-se as tensões de fase, pode-se
calcular as correntes de linha
(Lei de Ohm).

34. É importante destacar que, na
realidade, espera-se que nunca ocorra
um desligamento (rompimento) do
condutor neutro em qualquer instala-ção
elétrica, pois o rompimento do
condutor neutro pode resultar em
tensões de fase muito altas ou
baixas, comprometendo as condições de
operação de equipamentos conectados
entre uma fase e o neutro, sob pena
de serem danificados, dependendo da
localização do rompimento.
O rompimento do condutor neutro
não afeta as condições de operação
de equipamentos que estejam conec-tados
entre fases, como é o caso,
p. ex. de um chuveiro conectado
entre duas fases, pois se conside-ra
que as tensões fornecidas pela
companhia distribuidora são equi-libradas
e independem da carga
conectada.

35. Vídeos:
Tensões Trifásicas
http://www.youtube.com/watch?v=22434JHXYjs
Carga Trifásica em Estrela Desequilibrada
http://www.youtube.com/watch?v=22434JHXYjs