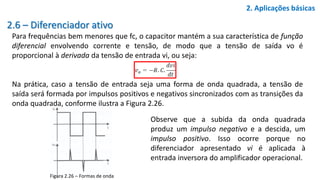
1) O documento descreve as características e aplicações do amplificador operacional (AO). O AO pode realizar operações matemáticas e funções como amplificação. 2) São descritas as principais características do AO, como ganho de tensão muito elevado, impedância de entrada alta e impedância de saída baixa. 3) Aplicações básicas do AO são descritas, incluindo amplificador inversor, não inversor, somador de tensão, subtrator de tensão e outros. Exemplos resolvidos ilustram o

1. Amplificador Operacional
Eletrônica
Prof. Reinaldo

2. Sumário
1. Introdução, características e especificações principais dos A.O.
2. Aplicações básicas e exercícios resolvidos
2.1 – Amplificador Inversor
2.2 – Amplificador Não Inversor
2.3 – Somador de tensão
2.4 – Subtrator de tensão
2.5 – Comparador de tensão
2.6 – Diferenciador ativo
2.7 – Integrador ativo

3. 1.1 - Principais características do Amplificador Operacional (A.O.)
O amplificador operacional (AO) é um dispositivo que pode realizar operações
matemáticas como adição, subtração, multiplicação, divisão, diferenciação, integração e
logaritmo, além de outras funções como comparação e amplificação. A Figura 1 ilustra o
símbolo do amplificador operacional.
1. Características e especificações
Figura 1.1 – Amplificador Operacional
O amplificador operacional é, na realidade, um circuito
complexo composto de inúmeros transistores, diodos e
resistores encapsulados como um circuito integrado.
Comercialmente, há diversos tipos de circuitos
integrados de amplificadores operacionais.
A Figura 1.1 mostra algumas características físicas do
AO. Ele possui duas entradas: a inversora (V-) e a não
inversora (V+), uma saída (Vo) e dois terminais de
alimentação: um positivo (+Vcc) e outro negativo
(-Vcc).
V-
V+
Vo
+Vcc
-Vcc
-
+

4. 1.1 - Principais características do Amplificador Operacional (A.O.)
Alguns AO só funcionam de forma adequada quando alimentados por tensão simétrica,
isto é, com potenciais positivo e negativo em relação ao terra (GND) do circuito.
1. Características e especificações
Figura 1.2 – Circuito equivalente do
amplificador operacional
Existem outros tipos que permitem que o terminal
negativo (-Vcc) seja conectado no próprio GND.
O circuito elétrico equivalente do amplificador
operacional é ilustrado na Figura 1.2.
Nele estão caracterizadas as suas principais
especificações, a saber: entrada diferencial (Ve = V+ -
V-), impedância de entrada (Zi), ganho de tensão (Ao) e
impedância de saída (Zo).
A operação básica do amplificador operacional é a
amplificação da tensão diferencial das entradas, ou
seja:
Vo = Ao.(V+ - V-) ou Vo = Ao.Ve
Zi
Zo
+
-
Ao.Ve VoVe
V+
V-

5. 1.2 - Principais especificações do Amplificador Operacional (A.O.)
O AO apresenta as seguintes especificações principais:
a) Impedância de Entrada – Zi
No amplificador operacional ideal, a impedância de entrada é infinita, o que garante
uma sensibilidade máxima, isto é, qualquer tensão diferencial aplicada às suas
entradas, por menor que seja, é amplificada.
No amplificador operacional real, a impedância de entrada é extremamente alta,
desde algumas dezenas de quilo ohms até dezenas de megaohms.
b) Impedância de Saída – Zo
No amplificador operacional ideal, a impedância de saída é nula, o que garante um
máximo rendimento do amplificador em relação ao sinal amplificado, de modo que
todo ele seja transferido à carga.
No amplificador operacional real, a impedância de saída é muito baixa, desde
algumas unidades de ohms até algumas centenas de ohms.
1. Características e especificações

6. 1.2 - Principais especificações do Amplificador Operacional (A.O.)
O AO apresenta as seguintes especificações principais:
c) Ganho de Entrada – Zi
No amplificador operacional ideal, o ganho de tensão em malha aberta é infinito,
garantindo amplificação máxima de qualquer diferença entre as tensões aplicadas aos
terminais de entrada.
No amplificador operacional real, o ganho de tensão em malha aberta é muito
elevado, desde algumas centenas a milhares de vezes.
d) Largura de Banda - LB
No amplificador operacional ideal, a largura de banda é infinita, ou seja, todos os
sinais de entrada são amplificados, desde sinais DC até AC de frequência infinita.
No amplificador operacional real, a largura de banda é relativamente alta, desde DC
até AC com centenas de mega-hertz, no entanto, o ganho de tensão cai com o
aumento de frequência, conforme ilustra a Figura 1.3
1. Características e especificações

7. 1.2 - Principais especificações do Amplificador Operacional (A.O.)
e) Tensão de off-set
No amplificador operacional ideal, a tensão de saída é nula para tensões de entrada
iguais ou nulas.
No amplificador operacional real, mesmo que as entradas estejam aterradas, há
tensão na saída, devido às imperfeições dos dispositivos que o compõem.
1. Características e especificações
Figura 1.3 – Largura de banda de um amplificador operacional

8. 1.3 – Alimentação de Amplificadores Operacionais
A alimentação simétrica de um amplificador operacional, quando necessária, pode
ser obtida de diferentes formas.
A primeira, e mais simples, é por meio de uma fonte de alimentação simétrica, isto é,
que tenha duas saídas, uma positiva (+Vcc) e outra negativa (-Vcc), em relação a uma
terceira saída GND.
Há, entretanto, formas de obter a tensão simétrica a partir de fonte de alimentação
simples, como ilustram as Figuras 1.4(a) e 1.4(b).
1. Características e especificações
Figura 1.4 – Fonte simétrica via fontes simples
(a) Utilizando duas fontes simples (b) Utilizando divisor resistivo
A tensão máxima de saída do
amplificador operacional é limitada à
tensão de alimentação. Na prática, as
tensões positiva e negativa são limitadas
pelos valores de saturação, isto é, +Vsat
e –Vsat, que normalmente são maiores
do que 90% de Vcc.

9. 2.1 – Amplificador Inversor
Nesta primeira aplicação do amplificador operacional, faremos algumas considerações
para tornar possível a sua análise.
O amplificador inversor tem a entrada de sinal ligada ao terminal inversor por meio de
um resistor R1 e o terminal não inversor aterrado. Entre os terminais de saída do inversor,
há um resistor de realimentação R2, conforme mostra o circuito da Figura 2.1.
2. Aplicações básicas
Figura 2.1 – Amplificador Inversor

10. 2.1 – Amplificador Inversor
Como vimos, o amplificador operacional possui uma
impedância de entrada muito alta, de modo que a
corrente que flui por R1 é desviada diretamente para
R2.
(1)
Mas, em princípio, a tensão Vo é o resultado da
amplificação. Ao da tensão diferencial de entrada,
representada por Ve, ou seja:
2. Aplicações básicas
Figura 2.1 – Amplificador Inversor

11. 2.1 – Amplificador Inversor
Como o amplificador operacional possui um ganho de
tensão muito elevado, no limite, podemos afirmar que
se Ao  ∞, então Ve  0.
Sendo Ve = 0, é como se o terminal V- estivesse
aterrado, tal como V+. Portanto, dizemos que o
terminal V- comporta-se como um terra virtual.
Voltando à expressão (1), obtemos:
A relação Vo/Vi reflete a amplificação do sinal
efetivamente aplicado na entrada do circuito (Vi).
2. Aplicações básicas
Figura 2.1 – Amplificador Inversor

12. 2.1 – Amplificador Inversor
Por ser um circuito composto por um resistor de
realimentação entre a saída e a entrada (R2), essa
relação é denominada de ganho de tensão de malha
fechada, que representamos por Av.
Assim , o ganho do amplificador inversor é dado por:
O sinal negativo na fórmula do ganho reflete a
inversão de fase que ocorre no sinal de saída em
relação ao sinal de entrada.
2. Aplicações básicas
Figura 2.1 – Amplificador Inversor

13. 2.1.1 – Exercícios resolvidos
Dado o circuito da Figura 2.2, determine a forma de
onda da tensão de saída, dados:
• R1 = 1kΩ /Vcc=± 12V
• R2 = 15kΩ /Vi = 200mV
• RL = 10k Ω
2. Aplicações básicas
Figura 2.2 – Aplicação do
Amplificador Inversor
Trata-se de um amplificador inversor, cujo ganho de tensão é:
A tensão de saída, nesse caso, vale:
A Figura 2.3 mostra as formas de onda na entrada e na saída.
Figura 2.3 – Formas de onda no circuito

14. 2.1.2 – Exercícios resolvidos
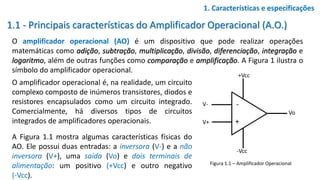
Determine a forma de onda das tensões de entrada e de saída do amplificador do
exercício anterior, caso vi = 500.cos(wt) [mV]
2. Aplicações básicas
Figura 2.2 – Aplicação do
Amplificador Inversor
Trata-se de um sinal cossenoidal cujo valor de pico é de 500 mV.
Nesse caso, o módulo da tensão de pico de saída vale:
Como o ganho é negativo, a expressão da tensão de saída será:
O sinal negativo indica que o sinal de saída possui uma inversão
de fase em relação ao sinal de entrada, conforme ilustra a Figura 2.4.
Figura 2.4– Formas de onda no circuito

15. 2.1.3 – Exercícios resolvidos
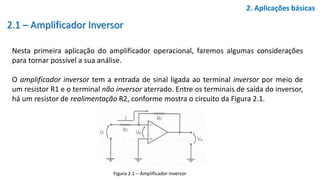
O que ocorreria no amplificador do exercício anterior, caso a tensão de entrada fosse
vi=2.cos(wt)[V], sabendo que a tensão de saída satura em 95% de Vcc.
2. Aplicações básicas
A tensão de saturação do amplificador operacional é a máxima
tensão que ele pode fornecer em sua saída, seja ela positiva ou
negativa.
Para esse amplificador operacional ela vale:
Vsat = ±0,95.Vcc  Vsat = ±0,95.12  Vsat = ±11,4V
Como o módulo do ganho desse circuito é 15, a máxima tensão
de entrada que pode ser aplicada ao amplificador sem que ele
sature vale:
No entanto, a tensão de pico na entrada é de 2V, de modo que o
sinal amplificado sairá distorcido, como indica a Figura 2.5
Figura 2.5– Formas de onda no circuito

16. 2.2 – Amplificador Não Inversor
O circuito do amplificador não inversor é ilustrado na Figura 2.6
2. Aplicações básicas
Figura 2.6 – Amplificador Não Inversor
Neste, o resistor da entrada inversora (R1) está aterrado e há também um resistor de
realimentação (R2) que liga a saída a entrada inversora. O sinal de entrada Vi é ligado
diretamente ao terminal não inversor, de modo que o sinal amplificado não terá fase
invertida.
Nesse amplificador, o ganho de tensão de malha fechada é dado por:

17. 2.2.1 – Exercício resolvido
1) Dado o circuito da Figura 2.7, determine a forma de onda da tensão de saída, dados:
• R1 = 1kΩ
• R2 = 15kΩ
• RL = 10kΩ
• Vcc =± 12V
• Vi = 200mV
2. Aplicações básicas
Figura 2.7 – Aplicação do Amplificador Não Inversor
Trata-se de um amplificador não inversor, cujo ganho de tensão é:
A tensão de saída, nesse caso, vale:
A Figura 2.8 ilustra as formas de onda na entrada
e na saída do circuito
Figura 2.8 – Formas de onda no circuito.

18. 2.2.2 – Exercício resolvido
2) Determine a forma de onda das tensões de entrada e de saída do amplificador do
exercício anterior, considerando vi = 500.cos(wt) [mV]
Trata-se de um sinal cossenoidal cujo valor de pico é de 500 mV. Nesse caso, o
módulo da tensão de pico de saída vale:
Assim, a expressão da tensão de saída será:
Ao contrário do que acontece na montagem anterior, no amplificador não inversor
não ocorre inversão de fase na saída, conforme mostra a figura 2.9
2. Aplicações básicas
Figura 2.9 – Formas de onda no circuito.

19. 2.3 – Somador de Tensão
O somador de tensão é basicamente um amplificador inversor com diversas entradas,
cada uma com um ganho que depende do valor do respectivo resistor, conforme ilustra a
figura 2.10.
A expressão da tensão de saída no caso em que R1=R2=R3=...=Rn é a seguinte:
Ainda, caso R = Rn, a expressão fica reduzida a:
2. Aplicações básicas
Figura 2.10 – Somador de tensão

20. 2.4 – Subtrator de Tensão
O subtrator de tensão é basicamente um amplificador diferencial com o mesmo ganho
nas entradas inversora e não inversora, conforme ilustra o circuito da Figura 2.11.
A expressão da tensão de saída é a seguinte:
Caso , a expressão da tensão de saída é:
Ainda, caso R1 = R2 = R3 = R4, a expressão fica reduzida a:
2. Aplicações básicas
Figura 2.11 – Subtrator de tensão

21. 2.4.1 – Exercícios resolvidos
1) Determinar a tensão de saída Vo dos circuitos apresentados em seguida:
• R1=10kΩ
• R2=10kΩ
• R3=10kΩ
• Vcc=±12V
• V1 = 1V
• V2 = 3V
Como R1 = R2 = R3 = 10kΩ, a tensão de saída vale:
Vo = -(V1+V2)  Vo = - (1 + 3)  Vo = -4V.
2. Aplicações básicas
Figura 2.12 – Aplicação do somador de tensão

22. 2.4.1 – Exercícios resolvidos
2) Determinar a tensão de saída Vo dos circuitos apresentados em seguida:
• R1=2,2kΩ
• R2=22kΩ
• R3=1kΩ
• R4=10kΩ
• Vcc=±12V
• V1 = 0,25V
• V2 = 1V
Neste exercício, trata-se de um subtrator de tensão:
Como R2/R1 = R4/R3 = 10, a tensão de saída vale:
Vo = 10.(V2-V1)  Vo = 10.(1-0,25)  Vo=7,5V
2. Aplicações básicas
Figura 2.13 – Aplicação do subtrator de tensão

23. 2.4.1 – Exercícios resolvidos
3) Determine as formas de ondas das tensões de entrada e de saída do exercício 1(a),
considerando-se V1= 1V e v2 = 3.sen(wt) [V]
Assim como no exercício 1, a tensão de saída vale:
vo = -(v1 + v2)  vo = -(1 + 3.sen(wt))  vo = -1 -3sen(wt) [V]
Nesse caso, a tensão de saída tem uma componente CC dada por V1 somada a uma
componente CA dada por v2. Tanto o sinal CC como o CA aparecem na saída
invertidos (ganho negativo), conforme ilustra a figura 2.14.
2. Aplicações básicas
Figura 2.14 – Formas de onda no circuito

24. 2.4.1 – Exercícios resolvidos
4) Dado o circuito a seguir, determine a expressão de saída (Vo) em função de A, B e C.
2. Aplicações básicas
Figura 2.15 – Circuito de aplicação
Cálculo de V1:
Trata-se da saída de um amplificador não inversor cuja expressão é dada por:
Cálculo de V2:
Trata-se da saída de um somador de tensão cuja expressão é dada por:

25. 2.4.1 – Exercícios resolvidos
4) Dado o circuito a seguir, determine a expressão de saída (Vo) em função de A, B e C.
2. Aplicações básicas
Figura 2.15 – Circuito de aplicação
Cálculo de Vo:
Na saída tem-se um subtrator de tensão cuja expressão é dada por:

26. 2.5 – Comparadores de Tensão
Há várias formas de se implementar um circuito comparador de tensão em função da
tensão de referência usada na comparação (zero, positiva ou negativa) e em função da
tensão de saída desejada após a comparação (zero, positiva ou negativa).
Como já mencionado anteriormente, o ganho de tensão do amplificador operacional em
malha aberta (sem realimentação) é muito elevado, portanto Vo terá dois valores
possíveis:
Vo = +Vsat quando V2 > V1
Vo = -Vsat quando V1 > V2
2. Aplicações básicas
Figura 2.12 – Circuito básico do comparador de tensão

27. 2.5 – Comparadores de Tensão
Vamos apresentar alguns tipos de comparadores que são suficientes para possibilitar a
implementação de diversos outros comparadores.
Cada comparador possui uma curva de transferência que representa o seu
comportamento, ou seja, que indica a tensão de saída a partir da tensão de entrada.
Comparadores de Zero
A Fig. 2.13(a) mostra o circuito comparador de zero não inversor, cuja saída é positiva
quando Vi >0 e negativa quando Vi <0. A Fig. 2.13(b) mostra a curva de transferência
desse comparador.
2. Aplicações básicas
Figura 2.13 – Comparador de zero não inversor

28. 2.5 – Comparadores de Tensão
Comparadores de Zero
A Fig. 2.14(a) mostra o circuito comparador de zero inversor, cuja saída é positiva quando
Vi < 0 e negativa quando Vi > 0. A Fig. 2.14(b) ilustra a curva de transferência desse
comparador.
2. Aplicações básicas
Figura 2.14 – Comparador de zero inversor

29. 2.5.1 – Exercícios resolvidos
Esboce os sinais de entrada e saída dos circuitos comparadores dados a seguir:
2. Aplicações básicas
Figura 2.15 – Circuito comparador
Dados:
• vi = 10.sen(wt) [V]
• Vcc = +/- 12V
• Vsat = +/- 95% de Vcc
Trata-se de um comparador de zero inversor no
qual Vo = -Vsat quando vi>0 e Vo = +Vsat
quando vi <0.
Como Vsat = +/- 0,95*12  Vsat = +/- 11,4V
A Figura 2.16 apresenta o esboço das formas de
onda desse circuito. Figura 2.16 – Formas de onda

30. 2.5.1 – Exercícios resolvidos
Esboce os sinais de entrada e saída dos circuitos comparadores dados a seguir:
2. Aplicações básicas
Figura 2.17 – Circuito comparador
Dados:
• vi = 10.sen(wt) [V]
• Vcc = +/- 12V
• Vsat = +/- 95% de Vcc
Trata-se de um comparador de zero não inversor
no qual Vo = +Vsat quando vi>0 e Vo = -Vsat
quando vi <0.
Como Vsat = +/- 0,95*12  Vsat = +/- 11,4V
A Figura 2.18 apresenta o esboço das formas de
onda desse circuito. Figura 2.18 – Formas de onda

31. 2.5 – Comparadores de Tensão
Comparadores de Nivel
A Fig. 2.19(a) mostra o circuito comparador de nível não inversor, cuja tensão de
referência Vr é dada por um potenciômetro. Nesse circuito, a saída é positiva quando Vi >
Vr e negativa quando Vi < Vr. A Fig. 2.19(b) mostra a curva de transferência desse
comparador, considerando-se Vr > 0.
2. Aplicações básicas
Figura 2.19 – Comparador de nível não inversor

32. 2.5 – Comparadores de Tensão
Comparadores de Nivel
Na Fig. 2.20(a) observa-se o circuito comparador de nível inversor, cuja tensão de
referência Vr é também positiva, mas cuja saída é positiva quando Vi < Vr e negativa
quando Vi > Vr. A Fig. 2.20(b) mostra a curva de transferência desse comparador.
Note que, nos dois circuitos comparadores de nível, pode-se ajustar Vr de +Vcc a –Vcc de
acordo com a necessidade do projeto.
2. Aplicações básicas
Figura 2.20 – Comparador de nível inversor

33. 2.5.2 – Exercícios resolvidos
Esboce os sinais de entrada e saída dos circuitos comparadores dados a seguir:
2. Aplicações básicas
Figura 2.21 – Circuito comparador
Dados:
• vi = 10.sen(wt) [V]
• Vcc = +/- 12V
• Vsat = +/- 95% de Vcc
• Vr = 7V
Trata-se de um comparador de nível inversor no
qual Vo = -Vsat quando vi>7V e Vo = +Vsat
quando vi <7V.
Como Vsat = +/- 0,95*12  Vsat = +/- 11,4V
A Figura 2.22 apresenta o esboço das formas de
onda desse circuito.
Figura 2.22 – Formas de onda

34. 2.5.2 – Exercícios resolvidos
Esboce os sinais de entrada e saída dos circuitos comparadores dados a seguir:
2. Aplicações básicas
Figura 2.23 – Circuito comparador
Dados:
• vi = 10.sen(wt) [V]
• Vcc = +/- 12V
• Vsat = +/- 95% de Vcc
• Vr = 7V
Trata-se de um comparador de nível não
inversor no qual Vo = +Vsat quando vi>7V e Vo =
-Vsat quando vi <7V.
Como Vsat = +/- 0,95*12  Vsat = +/- 11,4V
A Figura 2.24 apresenta o esboço das formas de
onda desse circuito. Figura 2.24 – Formas de onda

35. 2.6 – Diferenciador ativo
O diferenciador é um filtro passa-altas (FPA) cuja frequência do sinal de entrada é bem
menor do que a sua frequência de corte (f << fc).
Na Fig.2.25(a) observe o circuito do diferenciador ativo e na Fig.2.25(b) a sua curva de
resposta em frequência.
A frequência de corte desse circuito é dada por:
Para frequências maiores que fc, o capacitor comporta-se como um curto-circuito, de
modo que o circuito funciona como um amplificador inversor de ganho infinito, ou seja, a
tensão de saída é Vsat.
2. Aplicações básicas
Figura 2.25 – Diferenciador ativo

36. 2.6 – Diferenciador ativo
Para frequências bem menores que fc, o capacitor mantém a sua característica de função
diferencial envolvendo corrente e tensão, de modo que a tensão de saída vo é
proporcional à derivada da tensão de entrada vi, ou seja:
Na prática, caso a tensão de entrada seja uma forma de onda quadrada, a tensão de
saída será formada por impulsos positivos e negativos sincronizados com as transições da
onda quadrada, conforme ilustra a Figura 2.26.
2. Aplicações básicas
Observe que a subida da onda quadrada
produz um impulso negativo e a descida, um
impulso positivo. Isso ocorre porque no
diferenciador apresentado vi é aplicada à
entrada inversora do amplificador operacional.
Figura 2.26 – Formas de onda

37. 2.7 – Integrador ativo
O integrador é um filtro passa-baixas (FPB) cuja frequência do sinal de entrada é bem
maior do que a sua frequência de corte (f >> fc).
Na Fig.2.27(a) observe o circuito do integrador ativo e na Fig.2.27(b) a sua curva de
resposta em frequência.
A frequência de corte desse circuito é dada por:
Para frequências menores que fc, o capacitor comporta-se como uma alta impedância, de
modo que o circuito funciona como um amplificador inversor de ganho muito elevado, ou
seja, a tensão de saída é Vsat.
2. Aplicações básicas
Figura 2.27 – Integrador ativo

38. 2.7 – Integrador ativo
Para frequências bem maiores que fc, o capacitor mantém a sua característica de função
integral envolvendo corrente e tensão, de modo que a tensão de saída vo é proporcional
à integral da tensão de entrada vi, ou seja:
Na prática, caso a tensão de entrada seja uma forma de onda quadrada, a tensão de
saída terá o aspecto de uma onda triangular, conforme ilustra a Fig.2.28
2. Aplicações básicas
Figura 2.28 – Formas de onda
Observe que a onda triangular é crescente
quando a tensão de entrada é negativa e
decrescente, quando a tensão de entrada é
positiva, pelo fato de ser aplicada à entrada
inversora do amplificador operacional.

39. REFERÊNCIA BIBLIOGRÁFICA
Cruz, Eduardo Cesar Alves; Choueri Jr, Salomão. Eletrônica Aplicada –
2ª edição, Editora Érica, São Paulo, 2013