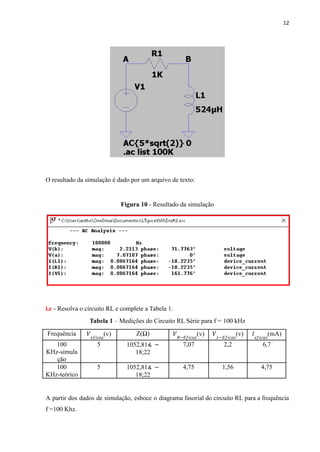
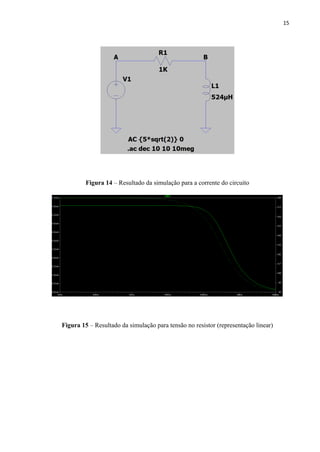
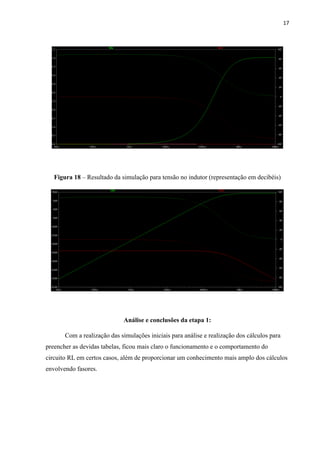
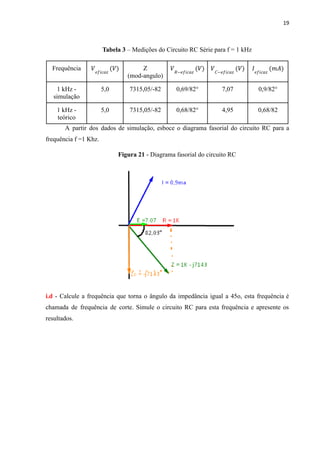
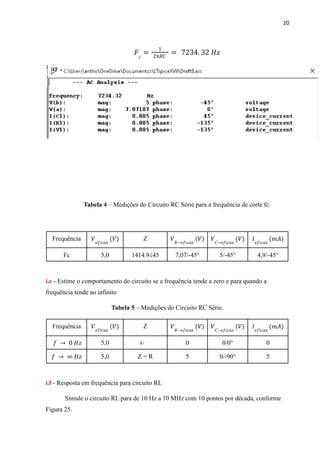
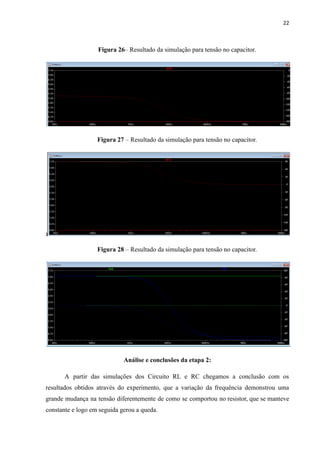
Este relatório analisa circuitos RL e RC simulados no LTspice. Para o circuito RL a 1 kHz, a corrente e tensão no indutor estão adiantadas em relação à tensão no resistor. Para o circuito RC a 1 kHz, a tensão no capacitor está atrasada em relação à tensão no resistor. Ambos os circuitos são simulados também na frequência de corte, onde a impedância forma um ângulo de 45 graus.

1. Serviço Público Federal
Ministério da Educação
Fundação Universidade Federal de Mato Grosso do Sul
Fundação de Engenharias, Arquitetura e Urbanismo e Geografia – FAENG
Engenharia Elétrica – Bacharelado
RELATÓRIO CIRCUITOS ELÉTRICOS 1
CIRCUITOS ELÉTRICOS
PRÁTICA N° 3
Professor: Nicolau Pereira Filho
Acadêmicos: Anthony Gabriel Leite de Lima, Laura Aguiar Vermieiro, Tássia Freitas Costa.
Campo Grande – MS
2022

2. RELATÓRIO CIRCUITOS ELÉTRICOS 1
CIRCUITO RL E RC
PRÁTICA N° 3
Acadêmicos: Anthony Gabriel Leite de Lima, Laura Aguiar Vermieiro, Tássia Freitas Costa.
Campo Grande – MS
2022

3. SUMÁRIO
OBJETIVOS 4
INTRODUÇÃO TEÓRICA 5
ANÁLISE E CONCLUSÃO ETAPA 1 17
ANÁLISE E CONCLUSÃO ETAPA 2 21

4. 4
OBJETIVOS
.
Este relatório tem por objetivo analisar e estudar circuitos montados em uma nova
ferramenta introduzida aos estudos da matéria, o LTspice. Utilizando desta ferramenta é
possível observar graficamente o comportamento da corrente, tensão e outros componentes.
Assim obtendo uma dimensão mais numérica de como a energia se comporta no circuito.

5. 5
INTRODUÇÃO TEÓRICA
Reatância Capacitiva 𝑋𝐶
Um capacitor, quando percorrido por uma corrente elétrica alternada, oferece uma
oposição à passagem dela, imposta por campo elétrico, denominada reatância capacitiva. Essa
reatância capacitiva é inversamente proporcional à frequência da corrente, ao valor do
capacitor e é dada pela relação:
𝑋𝐶
=
1
ω𝐶
=
1
2π𝑓𝐶
À medida que a frequência aumenta, a reatância capacitiva decresce até atingir um valor
praticamente nulo.
Reatância Indutiva 𝑋𝐿
Um indutor, quando percorrido por uma corrente elétrica alternada, oferece uma
oposição à passagem dela, imposta por campo magnético, denominada reatância indutiva.
Essa reatância indutiva é diretamente proporcional à frequência da corrente, ao valor do
indutor e é dada pela relação:
𝑋𝐿
= ω𝐿
= 2π𝑓𝐿
A reatância indutiva aumenta com a frequência.
Diagrama das impedâncias
Figura 1 – Diagrama Fasorial das Impedâncias

6. 6
Circuito R e L em CA
Considere-se o circuito RL série alimentado por uma fonte de tensão alternada
sinusoidal cuja tensão é descrita pela expressão.
Figura 2 – Esquema do circuito RL série
Conhecidos os valores de R e L, pretende determinar-se o regime permanente da
evolução temporal da corrente no circuito, i(t), e das tensões aos terminais da resistência, U R
(t), e da indutância, U L (t). Através da Lei das malhas, a soma da tensão aos terminais da
resistência, com a tensão aos terminais da bobine, igualará a tensão da fonte:
𝐸 𝑡
( ) = 𝑈𝑅
𝑡
( ) + 𝑈𝐿
(𝑡)
Em termos de amplitudes complexas a expressão anterior escreve-se:
𝐸 = 𝑅𝐼 + 𝐽ω𝐿𝐼
𝐸 = (𝑅 + 𝐽ω𝐿) 𝐼
Onde R + jωL representa a impedância complexa da resistência em série com a
indutância. Cujo módulo é dado por:
𝑧
| | = 𝑅
2
+ ω𝐿
( )
2

7. 7
Figura 3 – Diagrama vetorial
As amplitudes complexas da tensão da fonte e corrente, está representado na figura
seguinte. Uma vez determinada a corrente, é imediato o cálculo das tensões aos terminais dos
elementos. O diagrama vectorial completo das tensões e corrente do circuito, encontra-se
representado na figura seguinte, onde se evidenciou a Lei das Malhas: a soma dos vectores 𝑈𝐿
e iguala o vector E
̅ .
𝑈𝑅
Figura 4 – Diagrama vectorial do circuito RL série

8. 8
A amplitude complexa representando a tensão aos terminais da resistência é
𝑈𝑅
colinear com I̅ , isto é, tensão e corrente aos terminais da resistência, estão em fase.
Relativamente à amplitude complexa , representativa da tensão aos terminais da indutância,
𝑈𝐿
está adiantada π/2 relativamente I̅ , isto é, a tensão aos terminais da indutância está adiantada
π/2 relativamente à corrente que a percorre. Sendo que:
𝑈𝑅
| |= 𝑅 𝐼
| |
𝑈𝐿
| |= 𝑋𝐿
𝐼
| |
𝐸
| | = 𝑈𝑅
| |2
+ 𝑈𝐿
| |2
Circuito RC em CA em Regime permanente
Considere-se o circuito RC série alimentado por uma fonte de tensão alternada
sinusoidal cuja tensão é descrita pela expressão 𝐸 𝑡
( ) = 𝐸 𝑆𝑒𝑛(ω𝑡)
Figura 5 – Esquema do circuito RC série
Conhecidos os valores de R e C, pretende determinar-se o regime permanente da
evolução temporal da corrente no circuito, i(t), e das tensões aos terminais da resistência,

9. 9
UR(t), e da capacidade, UC(t). Através da Lei das malhas, a soma da tensão aos terminais da
resistência, com a tensão aos terminais da capacidade, igualará a tensão da fonte:
𝐸 𝑡
( ) = 𝑈𝑅
𝑡
( ) + 𝑈𝑐
(𝑡)
Em termos de amplitudes complexas a expressão anterior escreve-se:
𝐸 = 𝑅𝐼 +
1
𝐽ω𝐶
𝐼
𝐸 = (𝑅 + 𝐽
1
ω𝐶
) 𝐼
Em termos de amplitudes complexas a expressão anterior escreve-se:
Onde representa a impedância complexa da resistência em série com o capacitor.
𝑅 + 𝐽
1
ω𝐶
O diagrama vectorial das impedâncias, e amplitudes complexas da tensão da fonte e
corrente, está representado na figura seguinte.
Figura 6 – Diagrama vetorial
Uma vez determinada a corrente, é imediato o cálculo das tensões aos terminais dos
elementos: A amplitude complexa U
̅ R é colinear com I̅ , isto é, tensão e corrente aos terminais
da resistência, estão em fase. Relativamente à amplitude complexa U
̅ C, representativa da
tensão aos terminais da capacitância, está atrasada π/2relativamente I̅ , isto é, a tensão aos
terminais da capacitância está atrasada π/2 relativamente à corrente que a percorre. Sendo
que:

10. 10
𝑈𝑅
| |= 𝑅 𝐼
| |, 𝑒
𝑈𝑐
| |= 𝑋𝑐
𝐼
| |
𝐸
| | = 𝑈𝑅
| |2
+ 𝑈𝑐
| |2
O diagrama vectorial completo das tensões e corrente do circuito, encontra-se representado na
figura seguinte, onde se evidenciou a Lei das Malhas: a soma dos vectores U
̅ Le U
̅ R iguala o
vector E
̅ .
Figura 7– Diagrama vetorial do circuito RC série

11. 11
Parte experimental
Simulação i – Circuito RL em CA (regime permanente)
i.a - Monte o circuito elétrico da Figura 8 com R =1 kΩ e L = 524 µH no LTspice
Figura 8 – Circuito RL série
i.b -Simulação com LTSpice para frequência f=100 kHz apenas, conforme Figura 9
Figura 9 – Circuito RL série no LTspice para a frequência de 100 kHz

12. 12
O resultado da simulação é dado por um arquivo de texto:
Figura 10 - Resultado da simulação
i.c - Resolva o circuito RL e complete a Tabela 1.
Tabela 1 – Medições do Circuito RL Série para f = 100 kHz
Frequência (v)
𝑉𝑒𝑓𝑖𝑐𝑎𝑧
Z(Ω) (v)
𝑉𝑅−𝐸𝑓𝑖𝑐𝑎𝑧
(v)
𝑉𝐿−𝐸𝑓𝑖𝑐𝑎𝑧
(mA)
𝐼𝑒𝑓𝑖𝑐𝑎𝑧
100
KHz-simula
ção
5 1052,81∡ −
18;22
7,07 2,2 6,7
100
KHz-teórico
5 1052,81∡ −
18;22
4,75 1,56 4,75
A partir dos dados de simulação, esboce o diagrama fasorial do circuito RL para a frequência
f =100 Khz.

13. 13
Figura 11 – Diagrama vetorial do circuito RC _______
i.d - Calcule a frequência que torna o ângulo da impedância igual a 45°, esta frequência é
chamada de frequência de corte. Simule o circuito RL para esta frequência e apresente os
resultados.
𝐹𝑐 =
1
2π𝑅𝐿
= 303708𝐻𝑧

14. 14
Figura 12 - Resultado da simulação
Tabela 2 – Medições do Circuito RL Série para a frequência de corte fc.
Frequência (v)
𝑉𝑒𝑓𝑖𝑐𝑎𝑧
Z(Ω) (v)
𝑉𝑅−𝐸𝑓𝑖𝑐𝑎𝑧
(v)
𝑉𝐿−𝐸𝑓𝑖𝑐𝑎𝑧
(mA)
𝐼𝑒𝑓𝑖𝑐𝑎𝑧
fc 5 1414,21∡45 7 5 7
i.e - Estime o comportamento do circuito se a frequência tende a zero e para frequência
tendendo ao infinito
Frequência (v)
𝑉𝑒𝑓𝑖𝑐𝑎𝑧
Z(Ω) (v)
𝑉𝑅−𝐸𝑓𝑖𝑐𝑎𝑧
(v)
𝑉𝐿−𝐸𝑓𝑖𝑐𝑎𝑧
(mA)
𝐼𝑒𝑓𝑖𝑐𝑎𝑧
f🡪 0 Hz
5 Z=R 5 0 5
F🡪 ∞ Hz
5 ∞ 0 0 0
i.f - Resposta em frequência para circuito RL
Figura 13 – Circuito RL série no LTspice para 10 Hz a 10 MHz com 10 pontos por década.

15. 15
Figura 14 – Resultado da simulação para a corrente do circuito
Figura 15 – Resultado da simulação para tensão no resistor (representação linear)

16. 16
Figura 16 – Resultado da simulação para tensão no resistor (representação em decibéis)
Figura 17 – Resultado da simulação para tensão no indutor (representação linear)

17. 17
Figura 18 – Resultado da simulação para tensão no indutor (representação em decibéis)
Análise e conclusões da etapa 1:
Com a realização das simulações iniciais para análise e realização dos cálculos para
preencher as devidas tabelas, ficou mais claro o funcionamento e o comportamento do
circuito RL em certos casos, além de proporcionar um conhecimento mais amplo dos cálculos
envolvendo fasores.

18. 18
Simulação II – Circuito RC em CA (regime permanente)
i.a - Monte o circuito elétrico da Figura 13 com R =1 kΩ e C = 22 ƞF no LTspice.
Figura 19 – Circuito RC série
i.b - Simulação com LTSpice para frequência f = 1 kHz apenas, Conforme Figura 20.
Figura 20 – Circuito RC série no LTspice para a frequência de 1 kHz
i.c - Resolva o circuito RL e complete a Tabela 3.

19. 19
Tabela 3 – Medições do Circuito RC Série para f = 1 kHz
Frequência 𝑉𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) Z
(mod-angulo)
𝑉𝑅−𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) 𝑉𝐶−𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) 𝐼𝑒𝑓𝑖𝑐𝑎𝑧
(𝑚𝐴)
1 kHz -
simulação
5,0 7315,05/-82 0,69/82° 7,07 0,9/82°
1 kHz -
teórico
5,0 7315,05/-82 0,68/82° 4,95 0,68/82
A partir dos dados de simulação, esboce o diagrama fasorial do circuito RC para a
frequência f =1 Khz.
Figura 21 - Diagrama fasorial do circuito RC
i.d - Calcule a frequência que torna o ângulo da impedância igual a 45o, esta frequência é
chamada de frequência de corte. Simule o circuito RC para esta frequência e apresente os
resultados.

20. 20
𝐹𝑐
=
1
2π𝑅𝐶
= 7234. 32 𝐻𝑧
Tabela 4 – Medições do Circuito RC Série para a frequência de corte fc.
Frequência 𝑉𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) Z 𝑉𝑅−𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) 𝑉𝐶−𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) 𝐼𝑒𝑓𝑖𝑐𝑎𝑧
(𝑚𝐴)
Fc 5,0 1414.9∡45 7,07/-45° 5/-45° 4,9/-45°
i.e - Estime o comportamento do circuito se a frequência tende a zero e para quando a
frequência tende ao infinito
Tabela 5 – Medições do Circuito RC Série.
Frequência 𝑉𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) Z 𝑉𝑅−𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) 𝑉𝐶−𝑒𝑓𝑖𝑐𝑎𝑧
(𝑉) 𝐼𝑒𝑓𝑖𝑐𝑎𝑧
(𝑚𝐴)
𝑓 → 0 𝐻𝑧 5,0 ∞ 0 0/0° 0
𝑓 → ∞ 𝐻𝑧 5,0 Z = R 5 0/-90° 5
i.f - Resposta em frequência para circuito RL
Simule o circuito RL para de 10 Hz a 10 MHz com 10 pontos por década, conforme
Figura 25.

21. 21
Figura 22 -Circuito RC para resposta em frequência
Apresente e analise os gráficos da corrente do circuito, tensão no resistor e tensão no
indutor.
Figura 23 – Resultado da simulação para tensão no capacitor.
Figura 24 – Resultado da simulação para tensão no capacitor.
Figura 25 – Resultado da simulação para tensão no capacitor.

22. 22
Figura 26– Resultado da simulação para tensão no capacitor.
Figura 27 – Resultado da simulação para tensão no capacitor.
Figura 28 – Resultado da simulação para tensão no capacitor.
Análise e conclusões da etapa 2:
A partir das simulações dos Circuito RL e RC chegamos a conclusão com os
resultados obtidos através do experimento, que a variação da frequência demonstrou uma
grande mudança na tensão diferentemente de como se comportou no resistor, que se manteve
constante e logo em seguida gerou a queda.

23. 23
Este relatório possui uma importância considerável de acordo com o objetivo de
estudo apresentado, visto que tal assunto ajuda na melhor compreensão do funcionamento dos
circuitos RL e RC.