9 potência elétrica em cc e ca

Análise de circuitos elétricos CC e CA Pedro Barros Neto
9 – POTÊNCIA ELÉTRICA
Força F - É uma grandeza vetorial que traduz a capacidade de produzir o movimento ou a
deformação mecânica de um corpo. Unidade de medida no SI : Newton N ou Kg.m/s ² .
Significado mecânico: se uma massa de 1 Kg for acelerada em 1m/ s² sobre uma superfície
horizontal e sem atrito, essa massa estará sob uma força resultante horizontal de 1 Newton (2a
Lei
de Newton). O movimento horizontal e sem atrito desconsidera a interferência da força
gravitacional, que atua verticalmente.
Energia E – é a capacidade conservativa de um ente físico produzir trabalho, calor ou radiação.
Trabalho W (work) – é a transferência de energia entre dois sistemas. Unidade de medida no
SI : Joule J ou N.m ou Kg.m ²/s ² .
Mecanicamente: isso se traduz como cada metro de deslocamento horizontal de uma massa de 1 kg,
acelerada por 1 N.
Termicamente: 1 Caloria (4,186 J) é a energia dispendida para elevar a temperatura de 1g de água
de 14,5°C para 15,5 °C.
Eletricamente: 1 Joule é a energia dispendida para separar 1 Coulomb de cargas elétricas opostas,
no vácuo, para que haja entre elas um potencial de 1 Volt. E=Q.V , onde Q é a quantidade
de cargas elétricas em Coulomb e V a tensão elétrica em volt.
A energia elétrica é uma forma de energia intermediária, e das mais úteis, pois é fácil de gerar,
transportar, armazenar e utilizar. Pode ser produzida por:
• Gerador de indução eletromagnética, acionado mecanicamente por: motor de combustão
interna, motor a vapor (combustíveis fósseis, biomassa ou fissão nuclear), turbina
hidrelétrica e turbina eólica;
• Reação química: pilhas e baterias;
• Radiação luminosa: células fotovoltaicas;
Outras formas de energia também são medidas em Joule, por analogia com o equivalente trabalho
mecânico.
A energia do universo é constante, havendo somente a troca de energia entre sistemas interativos.
Na terra, as formas primárias são a radiação solar e a força da gravidade g .
Energia elétrica – é a potência elétrica acumulada no tempo: E= P.t .
Unidade de medida: Wh .
1

Potência elétrica P - significa a quantidade de energia elétrica Δ E produzida ou gasta num
intervalo de tempo Δt P=
Δ E
Δt
Unidade de medida: Watt W ou J /s .
POTÊNCIA ELÉTRICA EM CORRENTE CONTÍNUA
É uma grandeza escalar, onde:
• A potência de um elemento dissipativo é sempre positiva, dada pelo produto da resistência
(sempre positiva) pelo quadrado da corrente consumida, que pode ser algebricamente
positiva ou negativa P=±I2
. R (9.01).
• A potência fornecida por uma fonte, de corrente ou de tensão, é sempre negativa, resultado
direto do produto da elevação de tensão pela corrente fornecida P=Vr(I) (9.02).
Lembrando que a elevação de tensão tem sempre o sinal contrário ao da corrente.
Lei de Joule – a quantidade do calor fornecido por uma resistência elétrica é dada por:
Q =R. I2
.t (9.03).
NOTA: A máxima transferência de potência em CC já foi tratada o capítulo 4 – Fontes de
alimentação.
POTÊNCIA ELÉTRICA EM CORRENTE ALTERNADA SENOIDAL
Potência instantânea total, monofásica e sinusoidal
Para chegarmos na potência complexa S , vamos inicialmente estudar a potência total
instantânea, monofásica e sinusoidal S(ωt) , onde S é o módulo da potência total, ou potência
aparente.
A potência total instantânea é obtida com o produto da tensão instantânea pela corrente instantânea
S(ωt)=V (ω t).i(ω t) , considerando a frequência angular (ω ) .
Este cálculo nos levará a obter as componentes complexas (Real e Imaginária) da potência elétrica
em CA monofásica.
Dados: tensão e corrente instantâneas, em função das amplitudes r.m.s.:
v(ω t)=V sen(ω t) (9.04).
i(ω t)= I sen(ω t −ϕ ) (9.05).
2

Se considerarmos a tensão como referência de fase, e tomarmos as expressões (9.04) e (9.05),
podemos representar a potência total instantânea como o produto da tensão pela corrente:
S(ω t)=[V sen(ω t)].[ I sen(ω t −ϕ )] (9.06).
Para expandir a expressão (9.06), vamos utilizar a identidade trigonométrica que transforma produto
em soma de funções:
sen(a).sen(b)=
1
2
[cos(a−b)−cos(a+b)] e fazendo: a=ωt e b=(ωt+ϕ) , a expressão
(9.06) pode ser escrita como: S(ω t)=(V . I)cos[ω t−(ω t+ϕ )]−cos[ω t +(ω t +ϕ )] , cuja
simplificação, será:
• Primeiro termo cos[ω t−ω t +ϕ ]=cosϕ .
• Segundo termo cos[ω t +(ω t+ϕ )]=cos2ω t+ϕ sendo 2ω t o dobro da frequência
angular.
S(ω t)=V .I cosϕ −V .I cos(2ω t −ϕ ) (9-07).
Para encontrarmos a componente imaginária ± j Q , basta expandir a segunda parcela da
expressão (9.07), utilizando-se a identidade trigonométrica do cosseno da adição de dois arcos:
cos(a+b)=cosa.cosb−sen a. senb fazendo: a=2ωt e b=ϕ .
cos(2ω t +ϕ )=cos 2ω t .cosϕ −sen2ω t .senϕ Assim, a expressão (9.07) passa a ser escrita
como S(ω t)=V .I cosϕ −VI (cos2ω t .cosϕ −sen2ω t .senϕ )
S(ω t)=[V .I cosϕ −VI cosϕ .cos 2ω t ]−[VI senϕ .sen2ω t ] onde Q =V . I(sen±ϕ )
(9.08), então S(ω t)=[ P− Pcos 2ω t ]−[Q sen2ω t] (9-09).
O primeiro termo representa a parte real da potência total instantânea, com as duas componentes da
potência ativa:
• A primeira parcela mostra a potência ativa P=VI cosϕ (9.10) , sempre positiva e
independente do tempo, pois ω é constante. É o eixo da senoide S(ω t) , e representa o
equivalente ao nível CC da potência total .
• A segunda parcela P cos2ω t é a parte da potência ativa que oscila com o dobro da
frequência, no eixo P .
O segundo termo representa a parte imaginária da potência total, com a componente da potência
reativa Qsen2ω t em quadratura com a potência ativa ±
π
2
rad , oscilando também com o
dobro da frequência angular, mas no “eixo zero”.
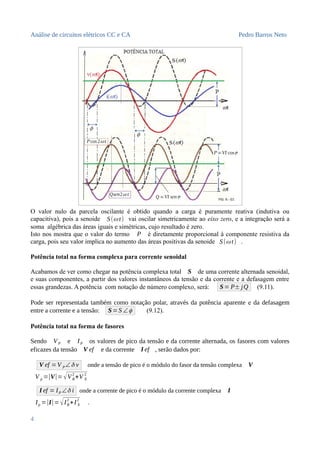
A “altura” da linha “P”, que é o eixo da senoide S(ω t) , dependerá da reatância presente no
circuito, e a “altura máxima” é obtida quando a carga é puramente resistiva (Fig. 9 - 03), pois a
senoide vai oscilar totalmente acima do “eixo zero”, e a sua integração será a soma das áreas
inteiramente positivas.
3

O valor nulo da parcela oscilante é obtido quando a carga é puramente reativa (indutiva ou
capacitiva), pois a senoide S(ω t) vai oscilar simetricamente ao eixo zero, e a integração será a
soma algébrica das áreas iguais e simétricas, cujo resultado é zero.
Isto nos mostra que o valor do termo P é diretamente proporcional à componente resistiva da
carga, pois seu valor implica no aumento das áreas positivas da senoide S(ω t) .
Potência total na forma complexa para corrente senoidal
Acabamos de ver como chegar na potência complexa total S de uma corrente alternada senoidal,
e suas componentes, a partir dos valores instantâneos da tensão e da corrente e a defasagem entre
essas grandezas. A potência com notação de número complexo, será: S= P± jQ (9.11).
Pode ser representada também como notação polar, através da potência aparente e da defasagem
entre a corrente e a tensão: S=S ∠ϕ (9.12).
Potência total na forma de fasores
Sendo VP e IP os valores de pico da tensão e da corrente alternada, os fasores com valores
eficazes da tensão V ef e da corrente I ef , serão dados por:
V ef =V P∠δ v onde a tensão de pico é o módulo do fasor da tensão complexa V
V p =|V|= √VR
2
+V X
2
I ef = IP ∠δ i onde a corrente de pico é o módulo da corrente complexa I
Ip =|I|=√IR
2
+I X
2
.
4

Inicialmente vamos abordar a potência total S como o produto dos fasores da tensão e da
corrente com valores r.m.s. Na multiplicação de dois fasores, a parte Real será o produto dos
módulos, e a parte Imaginária será a soma dos argumentos, aqui representados pelos respectivos
ângulos de defasagem:
S=V ef . I ef =VP. IP ∠δ v+δ i (9.13)
Como o ângulo de defasagem ϕ , da tensão em relação à corrente, é dado pela fase inicial da
tensão menos a fase inicial da corrente: ϕ =δv−δi , e não pela sua soma, como aparece em
(9.18), temos que utilizar o conjugado do fasor da corrente eficaz I
✴
ef , conforme já vimos no
tópico dos números complexos das ferramentas matemáticas para CA, onde: I
✴
ef =IP ∠−δ i .
Assim, a potência total é dada através do produto do fasor da tensão eficaz pelo “conjugado” do
fasor da corrente eficaz : S=V ef . I
✴
ef (9.14) que é o mesmo da expressão (9.11)
S= P± jQ . Em termos dos fasores com tensão e corrente de pico, a potência total será
S=
1
2
V .I∗
(9.15).
Potência total em função da tensão eficaz e do fasor da impedância complexa: S=
V
2
Z
(9.16).
Potência total em função da corrente eficaz e do fasor da impedância complexa: S= I
2
.Z (9.17)
ou S= I
2
(R± j X) (9.18).
Potência aparente para corrente senoidal S
É o módulo da potência complexa S , obtido pelo produto da parte Real da tensão eficaz V
pela parte Real da corrente eficaz I . Unidade de medida: VA (Volt-Ampere) e pode ser
medida com a utilização de um voltímetro e de um amperímetro com escala r .m .s. :
S =V . I (9.19).
Pode ser obtido por Pitágoras aplicado ao triângulo das potências: S =√P2
±Q2
(9.20).
Em função da corrente eficaz e do módulo da impedância: S =I
2
.Z (9.21).
Em função da tensão eficaz e do módulo da impedância: S =
V2
Z
(9.22).
Em função da potência eficaz e o FP: S =
P
cosϕ
(9.23).
Potência média, ou ativa, ou eficaz para corrente senoidal P
5

Ocorre quando houver qualquer componente resistivo nas cargas, pois isso vai criar a componente
“Real” da potência complexa total S , que representará a potência ativa dissipada pela carga:
P=|I
2
|RLD (9.24) ou P=
IP
2
2
RLD (9.25).
A potência ativa P é dada em Watt W e pode ser medida pelo instrumento Wattímetro.
Nota: A potência ativa sempre será menor ou igual à potência aparente: P≤ S
P=V . I cosϕ (9.10) ou P=S.cosϕ (9.26).
Potência Reativa Q para corrente senoidal
Ocorre sempre que houver qualquer carga reativa (indutiva ou capacitiva), pois isto vai criar a
componente “Imaginária” da potência total S , que representará a potência reativa trocada entre a
carga e o gerador, portanto não dissipada.
A potência reativa é dada em Volt Ampere Reativo VAR e pode ser medida pelo instrumento
Varímetro.
Q =V . I(sen±ϕ ) (9.08) , Q =S(sen±ϕ ) (9.27), Q =|I2
|.(± j X) (9.28) e
Q =
IP
2
2
(±j X) (9.29). Da expressão (9.16) S =
V
2
Z
se a impedância for puramente reativa,
teremos: Q =
V2
(±j X)
(9.30).
Triângulo das potências
A potência total complexa S (fig. 9 - 08):
6

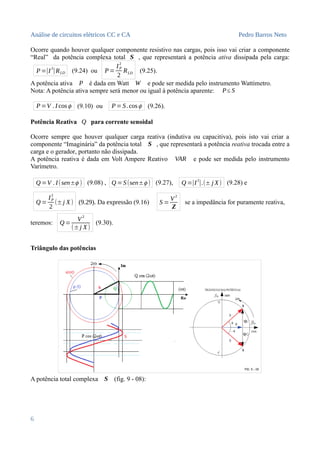
FATOR DE POTÊNCIA FP
A relação entre a potência ativa P e a potência aparente S é representada pelo valor do
cosseno do ângulo de defasagem ϕ entre a tensão e a corrente, que por sua vez é definido pelas
reatâncias presentes no circuito elétrico.
FP=
P
S
(9.31) FP=
V . I cosϕ
V .I
(9.32) FP=cosϕ (9.33).
O fator de potência também pode ser definido pela relação da resistência com o módulo da
impedância: FP=
R
Z
(9.34).
No circuito com predominância indutiva, a corrente está atrasada em relação à tensão, e assim
teremos: ϕ positivo e FP atrasado (lagging).
Exemplo: S=200 + j 40 com (9.25) S = √2002
+402
S =√40.000+1.600
S =203,96VA . Com (9.31) FP=
200
203,96
ou (9.33) FP=cosϕ =0,98 atrasado.
Ângulo de fase positivo ϕ =cos
−1
(0,98) ou ϕ =11,3° onde senϕ =0,196
No circuito com predominância capacitiva, a corrente está adiantada em relação à tensão, e assim
teremos: ϕ negativo e FP adiantado (leading).
Exemplo: S=200− j 40 com (9.25) S =√2002
+402
S =√40.000+1.600
S =203,96VA . Com (9.31) FP=
200
203,96
ou (9.33) FP=cosϕ =0,98 adiantado.
Ângulo de fase negativo ϕ =−[cos−
(0,98)] ou ϕ =−11,3° onde senϕ =−0,196 .
Notar que apenas o sinal do seno ficou negativo por ser uma função ímpar.
O FP ideal ocorre quando a carga é puramente resistiva, e assim teremos:
• a impedância será igual à resistência;
• o ângulo ϕ =0rd , e consequentemente cosϕ =1 .
• a potência ativa P será igual à potência aparente S , e a potência reativa Q será
nula.
As linhas de transmissão, de distribuição, e os circuitos consumidores são melhor utilizados quando
o fator de potência se aproxima do valor unitário, isto porque otimiza a capacidade de condução de
corrente efetiva.
Lembrando que a corrente reativa é utilizada para produzir campo magnético nas máquinas
indutivas, por isso não pode ser totalmente eliminada nos sistemas de corrente alternada, mas pode
ser atenuada através de compensadores capacitivos ligados onde há demanda de cargas indutivas.
7

A figura (9 - 09) nos mostra dois cenários:
1. Há uma carga indutiva “puxando” a potência total S1 para cima, criando a potência
reativa QL , e com isso, a potência ativa diminui para P1 . Neste cenário, uma parte da
corrente no circuito é improdutiva.
2. Ao instalar uma carga capacitiva, com reatância de módulo igual ao módulo da carga
indutiva, é criada a potência reativa QC que “empurra” a potência ativa P1 para a
posição P2 , e com isso, ela alcança seu valor máximo, igual à potência total S2 . Neste
cenário teórico, toda a corrente no circuito é convertida em trabalho.
Máxima transferência de potência em corrente alternada ou casamento de impedâncias:
Ocorre quando a impedância da carga for igual ao conjugado
complexo da impedância da fonte: ZG = ZLD
✴
(9.35).
Demonstração: No circuito da figura (9 - 09), temos:
V G = tensão eficaz do gerador (constante).
ZG = RG± j XG (9.36) impedância complexa do gerador
(constante).
ZLD = RLD± j XLD (9.37) impedância complexa da carga
(variável independente).
V LD = Tensão eficaz sobre a carga.
I =
VG
ZG+ZLD
(9.38) corrente eficaz.
Nas expressões (9.44) e (9.45) o termo imaginário refere-se às reatâncias, e será positivo para
cargas indutivas XL e negativo para cargas capacitivas XC .
Com as expressões (9.36) e (9.37) na expressão (9.38), teremos:
I =
VG
(RG+RLD)± j(XG+ XLD)
(9.39)
8

A potência ativa na carga é dada por (9.22): P=|I|2
RLD .
A potência total na carga é dada por (9.18) S= I
2
(R± j X) .
Para que a condição da expressão (9.43) seja satisfeita, teremos dois casos:
1. Carga ideal puramente resistiva, com ZLD =RLD : é intuitivo que a condição de
máxima transferência de potência para a carga ocorra quando o módulo da impedância do
gerador for igual à resistência da carga: ZG = RLD .
2. Carga mista, resistiva e reativa com (9.37) ZLD =RLD± j XLD : a reatância da carga
deverá ter o mesmo módulo da reatância do gerador, porém de tipos opostos, para anularem-
se e predominar somente a componente Real, que é a potência ativa P .
Exemplo 1:
Dado o circuito da figura 9 -11, calcular a capacitância C a ser ligada em paralelo com a carga,
para que haja a máxima transferência de potência do gerador para a carga.
Gerador:
• Tensão eficaz V G = 220V tensão de pico VP =V √2 ou VP =311,13V
• Frequência: f =60 Hz .
• Resistência das bobinas do estator: RG =10Ω
• Indutância do estator: LG =5mH
Carga:
• RLD =10Ω
• XLD a calcular.
Resolução: Impedância do gerador: ZG = RG+ j XG como RG já é dado, temos que calcular
o módulo da reatância indutiva, a partir da indutância dada:
XG =2π f L XG =6,28 x60 x 0,005H XG =1,884Ω .
Módulo da impedância do gerador:
ZG =√RG
2
+XG
2
ZG = √10
2
+1,884
2
ZG =√10
2
+1,884
2
ou ZG =10,176Ω .
Para definirmos a impedância em termos de fasores precisamos achar o ângulo de defasagem entre
a tensão e a corrente ϕ , calculado pela tangente do triângulo da impedância do gerador:
tan ϕ =
XG
RG
tan ϕ =
1,884
10
tan ϕ =0,189 onde ϕ =tan−1
0,189 ϕ =10,7° , então
teremos senϕ =0,18566 cosϕ =0,98 e ZG =10,176Ω ∠10,7° .
Para atender ao teorema da máxima transferência de potência, representado pela expressão (9.43), é
necessário apenas que XLD = XG =1,884Ω , haja vista que as resistências já são iguais.
9

O capacitor será calculado a partir da expressão da reatância capacitiva: XC =
1
2π fC
1,884=
1
6,28x 60xC
isolando C C=
1
6,28x 60 x1,884
C=
1
709,9
C=0,00140 F
ou C=1,4 μ F . Com essa capacitância teremos a impedância da carga igual ao conjugado da
impedância do gerador.
Impedância da carga: ZLD = RLD - j XC ZLD =10- j1,884Ω na forma polar
ZLD =10,176∠−10,7° .
Potências para FP= 1
Para calcular as potências, precisamos conhecer:
• A corrente eficaz com a tensão eficaz e os módulos das impedâncias I =
VG
ZG+ZLD
I =
220
10,176+10,176
ou I =10,81 A .
• A queda de tensão eficaz no gerador: VdG = I . ZG VdG =10,81 x10,176
VdG =110V .
• A queda de tensão eficaz na carga: VdLD = I . ZLD VdLD =10,81 x10,176
VdLD =110V .
Pela LTK , teremos: −VG+VdG+VdLD =0 −220+110+110 =0 .
Cálculo das potências
• Potência fornecida pelo gerador: S =P=−[ I2
ZG ] P=−[10,812
(10,176)] ou
P =−1.189,13W .
• Potência aparente do gerador S =P=−VG I P=−220 x10,81 P=−2.378,2 W .
• Potência dissipada no gerador S =P=VdG I P =110 x 10,81 P=1.189,1W .
• Potência dissipada na carga S =P= VdLD I P=110 x 10,81 P =1.189,1W .
10

Exemplo 2:
Dados do circuito na fig. 9 – 12
V =250V ∠0° (250V é convencionado como valor r.m.s. para este exemplo) ,
Zlinha =1+ j 4Ω e Zcarga =39 + j 26Ω .
Circuito em série, mas com a tensão adotada como referência de fase.
Questão (a) – calcular a corrente eficaz na carga.
Resposta (a) : O fasor da corrente, é: I =
V
Zlinha + ZLD
I =
250∠0°
(1+ j 4)+(39 + j 26)
I =
250∠ 0°
(40 + j 30)
simplificar I =
25∠0°
(4 + j3)
racionalizar I =
25(4− j 3)
(4 + j3)(4 − j 3)
I =
25(4 − j3)
25
ou I =(4− j 3) A e o conjugado I∗
=(4 + j 3) A .
A corrente eficaz na carga é a mesma do circuito, dada pelo módulo do fasor: I =√4
2
+ 3
2
I =√25 I =5 A . O argumento será θ =tan−1
(−3
4 ) θ =−36,87° adequando para
−j , teremos θ =323,43° . Então I =5∠323,43° A .
Questão (b) – calcular a queda de tensão eficaz na carga.
Resposta (b) : A queda de tensão eficaz complexa, é VLD = ILD (ZLD)
VLD =(4 − j 3)(39 + j 26) VLD =(156+78)+ j(104−117) ou VLD =234− j 13V . A
tensão eficaz é dada pelo módulo do fasor V =√−132
+2342
V =√169 +54.756
11

V =√54.925 V =234,36V . O argumento será θ =tan
−1
(−13
234 ) ou θ =−3,18°
adequando para −j , teremos θ =356,82° . Então V =234,36 ∠356,82°V .
Questão (c) - calcular a potência média e a potência reativa consumidas pela carga.
Resposta (c) - Já vimos que a potência total é dada através do produto do fasor da tensão eficaz
pelo “conjugado” do fasor da corrente eficaz:
S=V LD . ILD
∗
S=(234 − j13)(4 + j3) S=(975+ j 650)VA . O termo Real é a potência
média (eficaz) P =975 W . O termo imaginário é a potência reativa indutiva Q = j650 VAR .
O módulo da potência total será S =√975
2
+ 650
2
S =√950.625 + 422.500
S =√1.373.125 S =1.171,8VA . O argumento será θ =tan−1
(650
975) ou θ =33,69° .
S=1.171,8∠33,69° .
Questão (d) – calcular a potência média e a potência reativa, consumidas pela linha.
Resposta (d) - como a corrente do circuito é uma só, basta utilizar fórmulas das potências em
função da corrente eficaz: P=I2
Rlinha P=52
x1 ou P=25 W .
Q =I
2
.( XL) Q =5
2
( j 4) ou Q = j100 VAR .
Potencia eficaz consumida: P=975+ 25 ou P=1.000 W .
Potência reativa total: Q = j650 + j 100 ou Q = j750VA
Questão (e) - calcular a potência média e a potência reativa, fornecidas pela fonte.
Resposta (e) : Lembrando que a potência de uma fonte tem sinal negativo, pois está no sentido da
elevação de tensão V
−
→ V
+
.
Potência total com tensão e corrente eficazes S=−[V .I
∗
] , entrar com os valores
V =250V ∠0° e ILD
∗
=(4 + j3) A , então S=−[250(4 + j3)] ou
S=−1.000− j750 , onde P=−1.000 W e Q =− j750 VAR .
12

Exemplo 3:
Dados:
Cargas em paralelo
Carga 1: P1 =12 kW com FP=0,85 adiantado (carga capacitiva).
Carga 2: S2 =20kVA com FP=0,75 atrasado (carga indutiva).
Linha: Z=1 + j1Ω .
Tensão eficaz sobre as cargas: 220 V@ 60 Hz. Este valor fixo requer que a fonte tenha uma tensão
mais alta, e também regulada, para compensar as perdas da linha.
Pedem-se:
a) – Potência consumida nas cargas.
b) - FP resultante da carga.
c) –Corrente total e corrente eficaz nas cargas.
d) - Queda de tensão e potência consumida pela linha.
e) – Tensão regulada da fonte.
f) - Potência fornecida sem correção do FP.
g) – Capacitância para correção do FP.
h) – Valores alcançados com FP corrigido.
Resposta (a) – Potência consumida nas cargas
Cálculo de ϕ 1 : ϕ1 =cos
−1
0,85 ou ϕ1 =−31,78833° adequando para −j
ϕ =−328,21167° .
Carga 1: Módulo da potência total consumida pela carga 1 S1 =
P1
cosϕ1
S1 =
12.000
0,85
ou
S1 =14.117,647VA .
Potência reativa da carga 1: Q1 =S1(senϕ1) Q1 =14.117,647(−0,53) Q1 =−j 7.482VAR .
13

Potência Complexa da carga 1: S1 =12.000− j7.482VA .
Cálculo de ϕ 2 : ϕ2 =cos
−1
0,75 ou ϕ1 =41,41° .
Potência eficaz consumida pela carga 2: P2 =S2 cosϕ2
P2 =20.000(0,75) P2 =15.000W .
Potência reativa da carga 2: Q2 =S2(senϕ2) Q2 =20.000(0,66)
Q2 = j13.200VAR .
Potência Complexa da carga 2: S2 =15.000+ j13.200 .
Soma da potência total nas cargas:
S1,2 =(15.000 + 12.000) +( j13.200−j 7.482) ou
S1,2 = 27.000+ j 5.718VA com predominância indutiva (FP
atrasado).
Na forma polar, o módulo será: S1,2, = √27.0002
+ 5.7182
ou S1,2 =27.598,83VA ; o ângulo de
fase, será: tan ϕ1,2 =
5.718
27.000
tan ϕ1,2 =0,21778 ϕ1,2 = tan
−1
0,21778 ou ϕ1,2 = 11,957° .
Então a potência total, será: S1,2 =27.598,83∠ 11.96° VA .
Fig. 9 – 14 Triângulo das potências resultantes na carga.
Resposta (b): FP total da carga.
FPTOTAL=0,9783 .
Resposta (c): Corrente total e corrente eficaz nas cargas.
Como já temos a potência total e a tensão eficaz, a corrente total pode ser obtida a partir da
expressão (9.19) I
∗
=
S1,2
Vef
I
∗
=
27.000+ j5.718
220∠0°
I∗
=122,73 + j 26 ou
I =122,73− j26 A .
Na forma polar, o módulo da corrente complexa será: |I|= √122,732
+ 262
|I|=125,45 A . O
ângulo de fase da corrente é dado por: tg−1 26
122,73
ϕ I =tg−1
(0,21) ou ϕ I =11,96 ° (mesmo
resultado, já obtido anteriormente). Então teremos I =125,45 A ∠11,96° .
Corrente eficaz da carga 1: ILD 1=
P1
V
ILD 1=
12.000
220
ILD 1=54,545 A .
Corrente eficaz da carga 2: ILD 2=
P2
V
ILD 2=
15.000
220
ILD 2=68,182 A .
14

Soma das correntes eficazes nas cargas: I1,2 =122,73 A , que é a parte real da corrente
(complexa) total.
d) - Queda de tensão e potência consumida pela linha;
e) – Tensão regulada da fonte;
f) - Potência fornecida sem correção do FP.
g) – Capacitância para correção do FP.
h) – Valores alcançados com FP corrigido;
Resposta (d) - Queda de tensão e potência total consumida pela linha
VdLINHA =|I|RLINHA VdLINHA =125,45x 1 VdLINHA =125,45V .
Potência total consumida pela linha: da expressão (9.23) S= I
2
(R± j X)
SLINHA = 125,45
2
(1+ j1) SLINHA =15.737,7(1+ j 1) SLINHA =15.737,7 + j15.737,7 . Na
forma polar, o módulo será : S =√15.737,72
+15.737,72
S =√495.350.402,58 ou
S =22.256,47VA . O ângulo de fase, entre a corrente e a tensão, será obtido por:
tan ϕ =
15.737,7
15.737,7
tan ϕ =1 , então ϕ =tan
−1
1 ou ϕ =45° . A potência total
consumida, será: 22.256,47∠45° VA , com característica indutiva.
Resposta (e) - Tensão regulada da fonte
Tensão eficaz da fonte: Vg=−[VdLD + VdLINHA ] Vg=−[220 + 125,45] ou Vg=−345,45V .
Resposta (f) - Potência fornecida sem correção do FP.
Sf =−[SLINHA + S(1,2)] Sf =−[42.737,7+ j21.455,7] ou Sf =−42.737,7− j21.455,7VA
com característica capacitiva.
Resposta (g) - Capacitância para correção do FP nas cargas.
Precisamos definir qual será o módulo da reatância resultante das cargas, com predominância
indutiva. De Q1,2 =
V
2
X1,2
, tiramos X1,2 =
V
2
Q1,2
, então X1,2 =
220
2
5.718
ou X1,2 =8,44Ω ,
e esse valor será o módulo da reatância capacitiva necessária para corrigir o FP das cargas.
A partir de XC =
1
ω C
, onde ω =2π f e para 60 Hz ω =6,28∗60=377rad/s , vamos
achar o valor do capacitor C =
1
377(XC )
C=
1
377x 8,44
C =
1
377x 8,44
ou
C=0,000.314 F .
15

Assim, o FP corrigido ficará cosϕ =1 , e então teremos, da expressão (9.27) Scorrigido =
P
cosϕ
Scorrigido =
27.000
1
ou Scorrigido =27.000 . Então P=S= 27.000W .
Resposta (h) – Valores alcançados com FP corrigido
Com a correção do FP , as cargas comportam-se como puramente resistivas e a corrente total
corrigida, será:
Icorrigida = I =
P1,2
V LD
I =
27.000
220
ou I =122,727 A , que é menor do que a corrente total
anterior de 125,45 A .
Assim, haverá uma diminuição na perda de linha, com menor dispêndio de potência e menor tensão
na fonte.
Queda de tensão e potência total da linha:
VdLINHA = Icorrigida . RLINHA VdLINHA = 125,45x 1 VdLINHA =122,727V .
Potência total da linha: da expressão (9.21) S= Icorrigida
2
(R± j X) Sf =122,727
2
(1+ j 1)
SLINHA =15.061,916(1+ j 1) SLINHA =15.061,916+ j15.061,916 .
Potência total e tensão eficaz da fonte.
Potência total da fonte: Sf =−[SLINHA + S(1,2)] Sf =−42.061,916− j15.061,916 .
Tensão eficaz da fonte : Vg=−[V LD + VdLINHA ] Vg=−[220 + 122,727] ou
Vg=−342,727V .
Valores menores do que antes da correção do FP.
16

9 potência elétrica em cc e ca

Recomendados

Recomendados

Mais conteúdo relacionado

Mais procurados

Mais procurados (20)

Semelhante a 9 potência elétrica em cc e ca

Semelhante a 9 potência elétrica em cc e ca (20)

Mais de Pedro Barros Neto

Mais de Pedro Barros Neto (20)

Último

Último (7)

9 potência elétrica em cc e ca