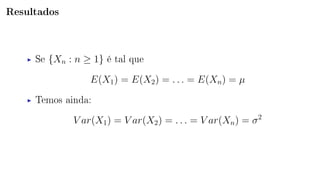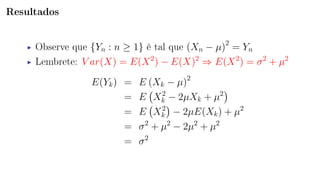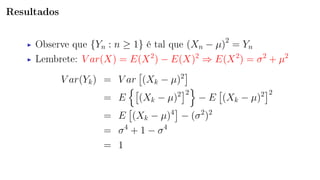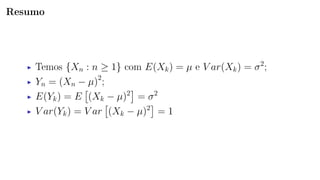Baixar para ler offline
Carregado porAnselmo Alves de Sousa
Teorema central do Limite - Exercício
O documento apresenta a resolução de uma questão sobre o Teorema Central do Limite. A questão envolve o cálculo do limite de uma probabilidade utilizando uma sequência de variáveis aleatórias i.i.d. O documento define a sequência, aplica o Teorema Central do Limite e mostra que a probabilidade converge para P(|Z| ≤ 1), onde Z é uma variável normal padrão.
Teorema central do Limite - Exercício
- 1.
- 3. Enunciado TeoremaCentral do Limite Questão: Seja {Xn : n ≥ 1} uma sequência de variáveis i.i.d com média µ e variância σ2 , para n ≥ 1, E(Xn − µ)4 = σ4 + 1. Use o Teorema Central do Limite e calcule lim n→∞ Pr 1 n n k=1 (Xk − µ)2 − σ2 ≤ 1 √ n
- 4. Teorema Central doLimite Seja {Xn : n ≥ 1} uma sequência de variáveis i.i.d com esperança µ e variância σ2 , com 0 σ2 ∞. Então para Sn = X1 + X2 + . . . + Xn temos: Sn − nµ σ √ n d −→ N(0, 1)
- 5. Resultados Se {Xn :n ≥ 1} é tal que E(X1) = E(X2) = . . . = E(Xn) = µ Temos ainda: V ar(X1) = V ar(X2) = . . . = V ar(Xn) = σ2
- 6. Resultados Observe que {Yn: n ≥ 1} é tal que (Xn − µ)2 = Yn Lembrete: V ar(X) = E(X2 ) − E(X)2 ⇒ E(X2 ) = σ2 + µ2 E(Yk) = E (Xk − µ)2 = E X2 k − 2µXk + µ2 = E X2 k − 2µE(Xk) + µ2 = σ2 + µ2 − 2µ2 + µ2 = σ2
- 7. Resultados Observe que {Yn: n ≥ 1} é tal que (Xn − µ)2 = Yn Lembrete: V ar(X) = E(X2 ) − E(X)2 ⇒ E(X2 ) = σ2 + µ2 V ar(Yk) = V ar (Xk − µ)2 = E (Xk − µ)2 2 − E (Xk − µ)2 2 = E (Xk − µ)4 − (σ2 )2 = σ4 + 1 − σ4 = 1
- 8. Resumo Temos {Xn :n ≥ 1} com E(Xk) = µ e V ar(Xk) = σ2 ; Yn = (Xn − µ)2 ; E(Yk) = E (Xk − µ)2 = σ2 V ar(Yk) = V ar (Xk − µ)2 = 1
- 9. Resolução TeoremaCentral do Limite Podemos reescrever Pr 1 n n k=1 (Xk − µ)2 − σ2 ≤ 1 √ n = Pr − 1 √ n ≤ 1 n n k=1 (Xk − µ)2 − σ2 ≤ 1 √ n = Pr − 1 √ n ≤ n k=1 (Xk − µ)2 − nσ2 n ≤ 1 √ n = Pr −1 ≤ n k=1 (Xk − µ)2 − nσ2 √ n ≤ 1 = Pr −1 ≤ n k=1 Yk − nσ2 √ n ≤ 1 = Pr (−1 ≤ Z ≤ 1) = P(|Z| ≤ 1) § ¦ ¤ ¥ A probabilidade inicial converge para Pr(|Z| ≤ 1), onde Z ∼ N(0, 1)
- 10. Enunciado TeoremaCentral do Limite Questão: Seja {Xn : n ≥ 1} uma sequência de variáveis i.i.d com média µ e variância σ2 , para n ≥ 1, E(Xn − µ)4 = σ4 + 1. Use o Teorema Central do Limite e calcule lim n→∞ Pr 1 n n k=1 (Xk − µ)2 − σ2 ≤ 1 √ n = P(|Z| ≤ 1)
- 11. Materiais Veja descrição dovídeo concurseiro_estatistico@outlook.com