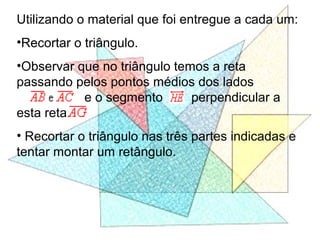
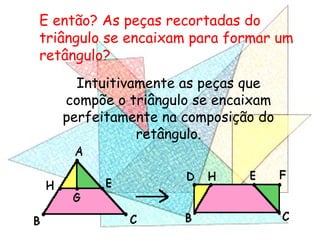
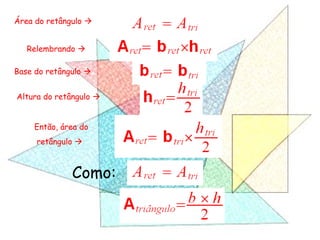
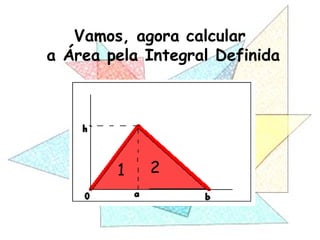
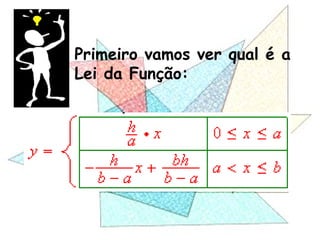
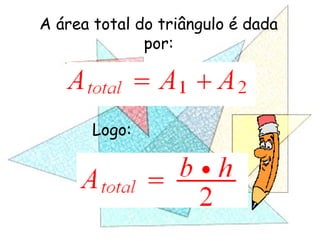
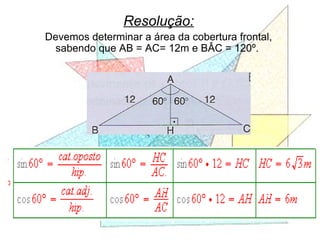
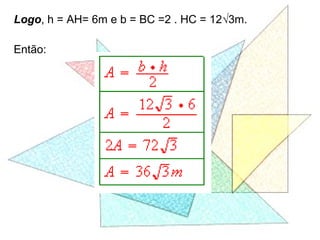
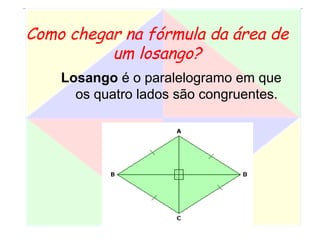
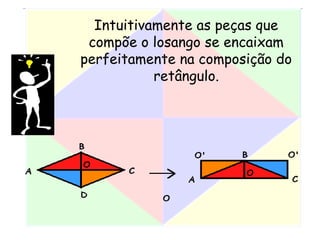
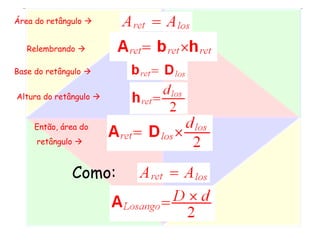
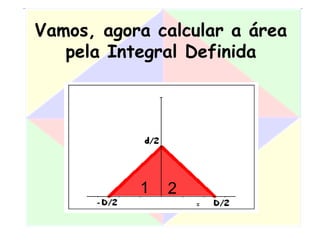
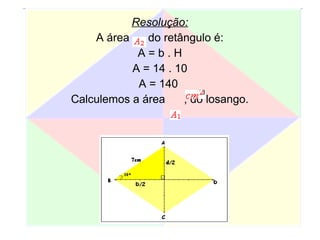
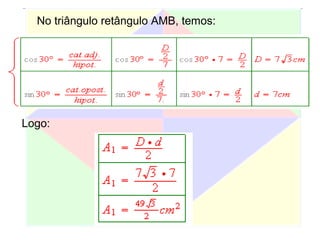
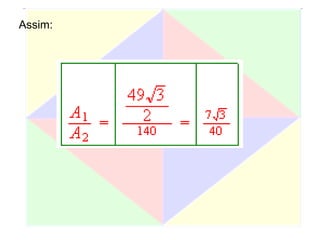
Este documento apresenta um resumo de uma aula prática sobre cálculo de áreas de figuras planas. Nele, discute-se como calcular as áreas de triângulos, losangos e retângulos por meio de decomposições em outras figuras e da integral definida. Também contém exemplos numéricos de aplicação desses conceitos.