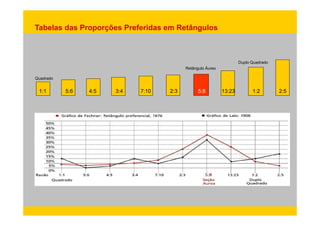
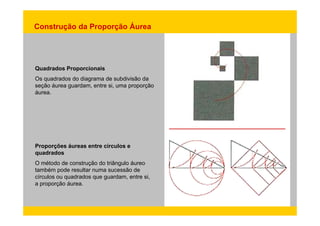
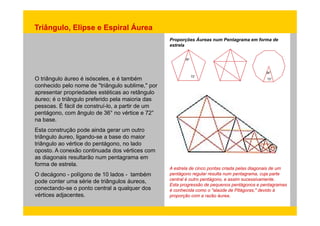
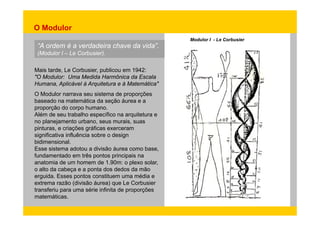
1) O documento discute como proporções geométricas como a seção áurea estão presentes na natureza e na arte, influenciando preferências estéticas humanas.
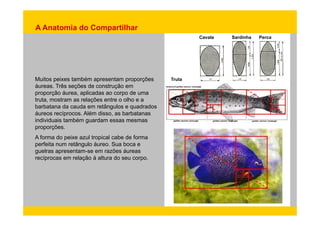
2) A seção áurea pode ser encontrada nos padrões de crescimento de conchas, plantas, animais e no corpo humano.
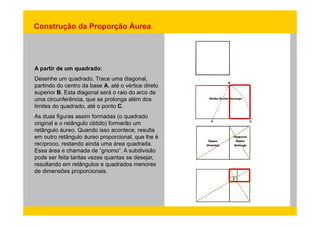
3) Artistas clássicos como Vitruvius usaram proporções baseadas na seção áurea em suas obras para criar formas harmonicas.