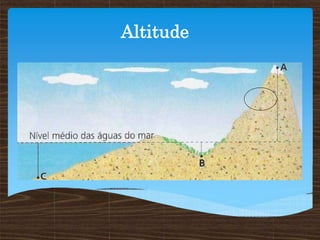
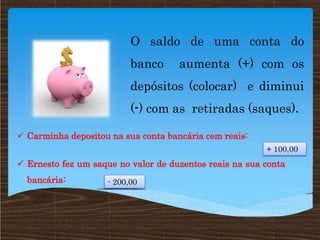
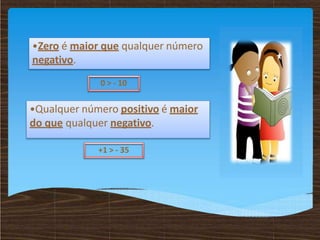
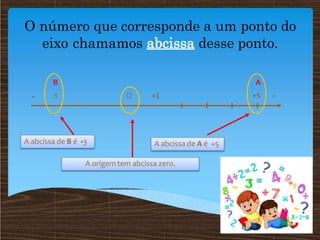
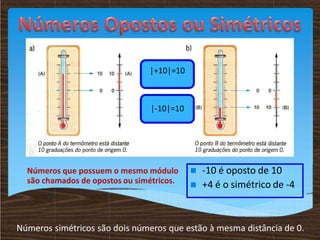
O documento discute conceitos matemáticos relacionados a números inteiros, incluindo sua representação na reta numérica, comparação e ordenação, opostos e valores absolutos. Exemplos mostram como números positivos e negativos podem ser usados para descrever situações como temperatura, saldo bancário e número de pessoas em um ônibus.