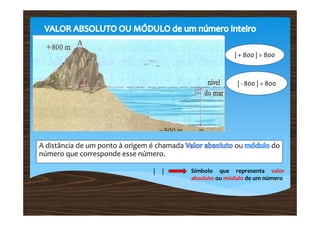
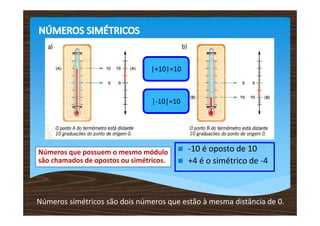
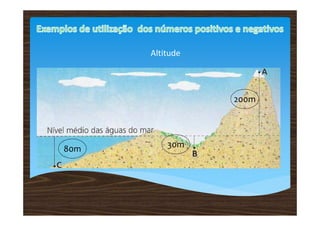
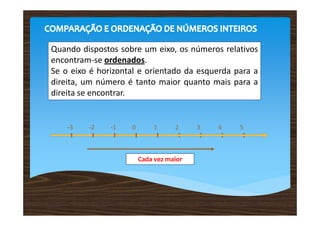
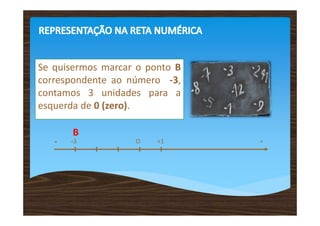
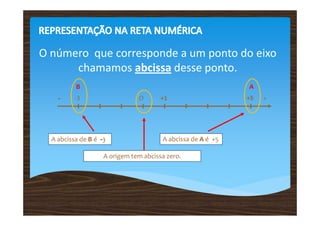
1) Os números inteiros relativos incluem todos os números inteiros negativos, o zero e todos os positivos. 2) Uma temperatura foi registrada como 10°C acima de zero e depois 3°C abaixo de zero, relacionando os números positivos e negativos. 3) Os números inteiros relativos podem ser representados em uma reta numérica, onde números mais à direita são maiores.

2. Os números inteiros relativos são
formados por todos os números inteiros
negativos, pelo zero e por todos os
números inteiros positivos.
Z = {..., -4, -3, -2, -1, 0, +1, +2, +3,...}
Ao conjunto dos números inteiros positivos, números inteiros negativos e
zero chamamos conjunto de números inteiros relativos.

3. Um termómetro em certa cidade que
marcou 10°C acima de zero durante o dia,
à noite e na manhã seguinte o
termómetro passou a marcar 3°C abaixo
de zero. Qual a relação dessas
temperaturas com os números inteiros?
Quando falamos acima de zero, estamos a
referir aos números positivos e quando
falamos dos números abaixo de zero
estamos a referir aos números negativos.
10° C ------------- 10° C acima de zero
- 3° C --------------- 3° C abaixo de zero

4. Chamamos a todos os que estão
abaixo de zero.
Os números negativos com o símbolo menos
antes.
Assim os diferenciamos dos positivos
..., -5, -4, -3, -2, -1
Quando um número não leva sinal
nenhum antes, entendemos que é
positivo:
6= +6 +12=12

6. Altitude
200m
80m 30m

7. Do andar em que se encontra
o elevador do edifício, posso
subir a pisos superiores ou
descer a outros pisos
inferiores:
•Subo cinco andares: +5
•Desço quatro andares: -4

8. O saldo de uma conta do banco
aumenta (+) com os depósitos
e diminui (-) com os
levantamentos.
• A Carminho depositou na sua conta bancária cem euros: + € 100
• O Ernesto levantou 200 euros da sua conta bancária: - € 200

9. O número de pessoas que viajam num
autocarro varia em cada paragem:
•Sobem 10 pessoas: + 10 pessoas
•Descem 14 pessoas: - 14 pessoas

10. Quando dispostos sobre um eixo, os números relativos
encontram-se ordenados.
Se o eixo é horizontal e orientado da esquerda para a
direita, um número é tanto maior quanto mais para a
direita se encontrar.
-3 -2 -1 0 1 2 3 4 5
Cada vez maior

11. Da observação da posição relativa de
dois números num eixo resultam
algumas regras para comparar dois
números diferentes:
•Qualquer número positivo é
maior do que zero.
+ 8,25 > 0 +3>0 + 4,5 > 0

12. •Zero é maior que qualquer número
negativo.
0 > - 10
•Qualquer número positivo é maior
do que qualquer negativo.
+1 > - 35

13. Que temperatura é a mais baixa: - 5 ºC, - 2 ºC ou + 2 ºC?
- 5 < - 2 < +2
Os números “crescem” da esquerda para a direita. Um
número é tanto maior quanto mais à direita se encontrar.
Para auxiliar na comparação usa sempre a reta numérica.

14. Depois da representação dos números numa reta numérica é fácil ordená-
los.
Para escrever os números por ordem crescente, basta-nos lê-los, na
reta numérica, da esquerda para a direita:
-9 < -4 < 0 < 1 < 2 < 4 < 9
Verificamos também que:
0 (zero) é menor do que qualquer número positivo.
Qualquer número negativo é menor que zero.
Qualquer número negativo é menor que qualquer número positivo.
Entre dois números negativos é menor o que estiver mais afastado da
origem.

15. Os números relativos – positivos,
negativos ou o zero – podem ser
representados numa reta por meio de
pontos.
Se quisermos marcar o ponto A correspondente ao número +5,
contamos 5 unidades para a direita de 0 ( zero ).
A
- O +1 +5 +

16. Se quisermos marcar o ponto B
correspondente ao número -3,
contamos 3 unidades para a
esquerda de 0 (zero).
B
- -3 O +1 +

17. O número que corresponde a um ponto do eixo
chamamos abcissa desse ponto.
B A
- -3 O +1 +5 +
A abcissa de B é -3 A abcissa de A é +5
A origem tem abcissa zero.

18. | + 800 | = 800
| - 800 | = 800
A distância de um ponto à origem é chamada ou do
número que corresponde esse número.
| | Símbolo que representa valor
absoluto ou módulo de um número

19. |+10|=10
|-10|=10
Números que possuem o mesmo módulo -10 é oposto de 10
são chamados de opostos ou simétricos. +4 é o simétrico de -4
Números simétricos são dois números que estão à mesma distância de 0.

20. (+4)+(+2)=(+6)
Sinais operacionais
Sinais posicionais
(-4)+(-2)=(-6)
Da adição de dois números relativos
com o mesmo sinal, resulta um
número com o mesmo sinal e cujo
valor absoluto é a soma dos valores
absolutos desses números.

21. (-3)+(+2)=(-1)
Sinais operacionais
Sinais posicionais
(+3)+(-2)=(+1)
Da adição de dois números relativos com sinais contrários, resulta
um número com o sinal do que tiver maior valor absoluto. O seu
valor absoluto é a diferença dos valores absolutos desses
números.

22. Será que só existem adições? Então e
a subtração (+2) - (+4) ?

23. Para subtrair dois números inteiros
relativos, adicionamos o aditivo com o
simétrico do subtractivo.
EXEMPLOS:
(+ 3) – (+ 5) = - 2 (+ 3) – (- 3) = + 6
(- 3) – (- 6) = +3 (- 5) – (- 3) = - 2

24. SUBCONJUNTOS DE Z :
Z+ = { 1, 2, 3, ...} → números inteiros positivos
Z - = {..., -3, -2, -1} → números inteiros negativos
Z 0+ = {0, 1, 2, 3, ...} → números inteiros não negativos
Z 0- = {..., -3, -2, -1, 0} → números inteiros não positivos